Alex Peysakhovich
Efficient Heterogeneous Treatment Effect Estimation With Multiple Experiments and Multiple Outcomes
Jun 10, 2022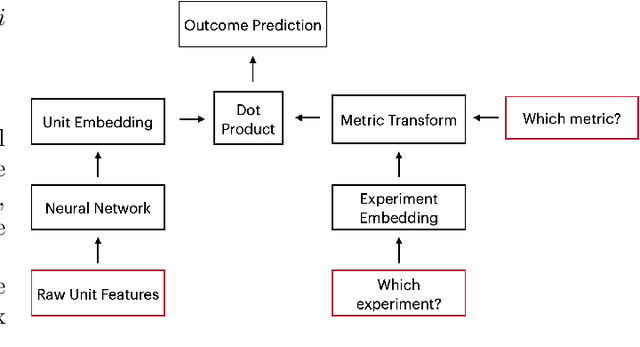
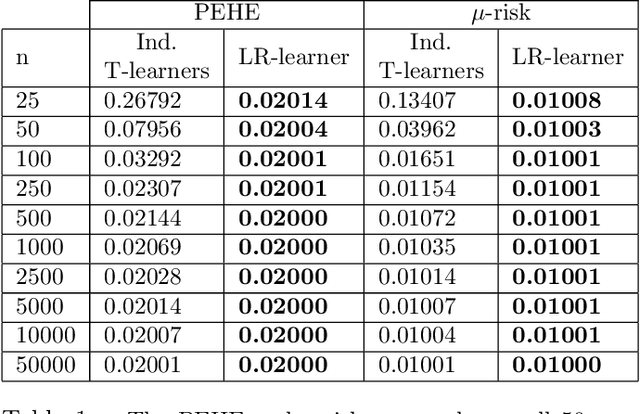
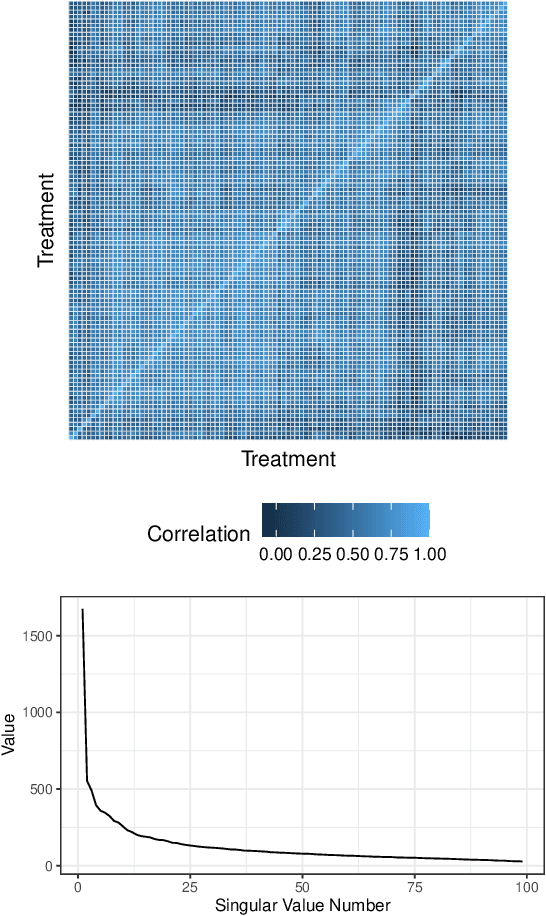
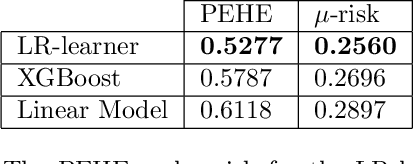
Abstract:Learning heterogeneous treatment effects (HTEs) is an important problem across many fields. Most existing methods consider the setting with a single treatment arm and a single outcome metric. However, in many real world domains, experiments are run consistently - for example, in internet companies, A/B tests are run every day to measure the impacts of potential changes across many different metrics of interest. We show that even if an analyst cares only about the HTEs in one experiment for one metric, precision can be improved greatly by analyzing all of the data together to take advantage of cross-experiment and cross-outcome metric correlations. We formalize this idea in a tensor factorization framework and propose a simple and scalable model which we refer to as the low rank or LR-learner. Experiments in both synthetic and real data suggest that the LR-learner can be much more precise than independent HTE estimation.
Ridge Rider: Finding Diverse Solutions by Following Eigenvectors of the Hessian
Nov 12, 2020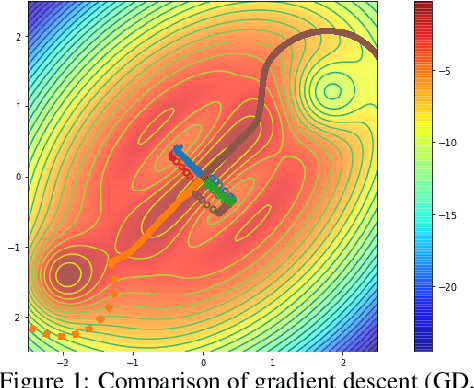
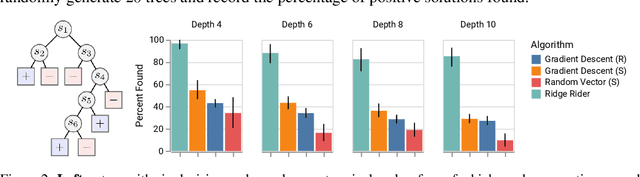
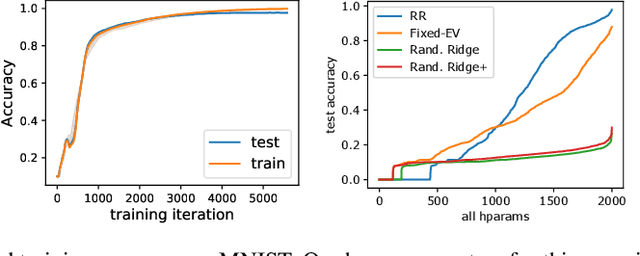
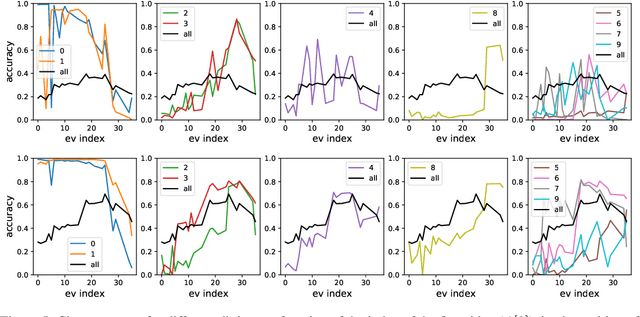
Abstract:Over the last decade, a single algorithm has changed many facets of our lives - Stochastic Gradient Descent (SGD). In the era of ever decreasing loss functions, SGD and its various offspring have become the go-to optimization tool in machine learning and are a key component of the success of deep neural networks (DNNs). While SGD is guaranteed to converge to a local optimum (under loose assumptions), in some cases it may matter which local optimum is found, and this is often context-dependent. Examples frequently arise in machine learning, from shape-versus-texture-features to ensemble methods and zero-shot coordination. In these settings, there are desired solutions which SGD on 'standard' loss functions will not find, since it instead converges to the 'easy' solutions. In this paper, we present a different approach. Rather than following the gradient, which corresponds to a locally greedy direction, we instead follow the eigenvectors of the Hessian, which we call "ridges". By iteratively following and branching amongst the ridges, we effectively span the loss surface to find qualitatively different solutions. We show both theoretically and experimentally that our method, called Ridge Rider (RR), offers a promising direction for a variety of challenging problems.
"Other-Play" for Zero-Shot Coordination
Mar 09, 2020



Abstract:We consider the problem of zero-shot coordination - constructing AI agents that can coordinate with novel partners they have not seen before (e.g. humans). Standard Multi-Agent Reinforcement Learning (MARL) methods typically focus on the self-play (SP) setting where agents construct strategies by playing the game with themselves repeatedly. Unfortunately, applying SP naively to the zero-shot coordination problem can produce agents that establish highly specialized conventions that do not carry over to novel partners they have not been trained with. We introduce a novel learning algorithm called other-play (OP), that enhances self-play by looking for more robust strategies, exploiting the presence of known symmetries in the underlying problem. We characterize OP theoretically as well as experimentally. We study the cooperative card game Hanabi and show that OP agents achieve higher scores when paired with independently trained agents. In preliminary results we also show that our OP agents obtains higher average scores when paired with human players, compared to state-of-the-art SP agents.
PyTorch-BigGraph: A Large-scale Graph Embedding System
Apr 09, 2019



Abstract:Graph embedding methods produce unsupervised node features from graphs that can then be used for a variety of machine learning tasks. Modern graphs, particularly in industrial applications, contain billions of nodes and trillions of edges, which exceeds the capability of existing embedding systems. We present PyTorch-BigGraph (PBG), an embedding system that incorporates several modifications to traditional multi-relation embedding systems that allow it to scale to graphs with billions of nodes and trillions of edges. PBG uses graph partitioning to train arbitrarily large embeddings on either a single machine or in a distributed environment. We demonstrate comparable performance with existing embedding systems on common benchmarks, while allowing for scaling to arbitrarily large graphs and parallelization on multiple machines. We train and evaluate embeddings on several large social network graphs as well as the full Freebase dataset, which contains over 100 million nodes and 2 billion edges.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge