Alistair Letcher
An Optimisation Framework for Unsupervised Environment Design
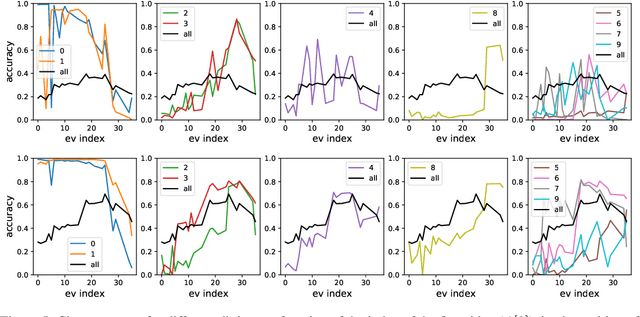
May 27, 2025Abstract:For reinforcement learning agents to be deployed in high-risk settings, they must achieve a high level of robustness to unfamiliar scenarios. One method for improving robustness is unsupervised environment design (UED), a suite of methods aiming to maximise an agent's generalisability across configurations of an environment. In this work, we study UED from an optimisation perspective, providing stronger theoretical guarantees for practical settings than prior work. Whereas previous methods relied on guarantees if they reach convergence, our framework employs a nonconvex-strongly-concave objective for which we provide a provably convergent algorithm in the zero-sum setting. We empirically verify the efficacy of our method, outperforming prior methods in a number of environments with varying difficulties.
Adversarial Cheap Talk
Nov 20, 2022



Abstract:Adversarial attacks in reinforcement learning (RL) often assume highly-privileged access to the victim's parameters, environment, or data. Instead, this paper proposes a novel adversarial setting called a Cheap Talk MDP in which an Adversary can merely append deterministic messages to the Victim's observation, resulting in a minimal range of influence. The Adversary cannot occlude ground truth, influence underlying environment dynamics or reward signals, introduce non-stationarity, add stochasticity, see the Victim's actions, or access their parameters. Additionally, we present a simple meta-learning algorithm called Adversarial Cheap Talk (ACT) to train Adversaries in this setting. We demonstrate that an Adversary trained with ACT can still significantly influence the Victim's training and testing performance, despite the highly constrained setting. Affecting train-time performance reveals a new attack vector and provides insight into the success and failure modes of existing RL algorithms. More specifically, we show that an ACT Adversary is capable of harming performance by interfering with the learner's function approximation, or instead helping the Victim's performance by outputting useful features. Finally, we show that an ACT Adversary can manipulate messages during train-time to directly and arbitrarily control the Victim at test-time.
Discovered Policy Optimisation
Oct 13, 2022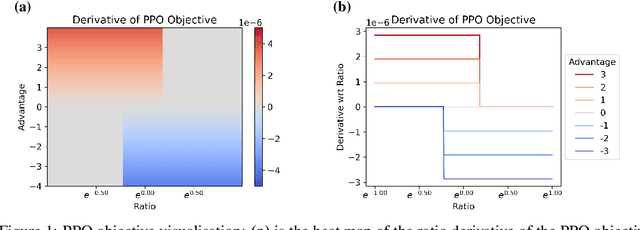
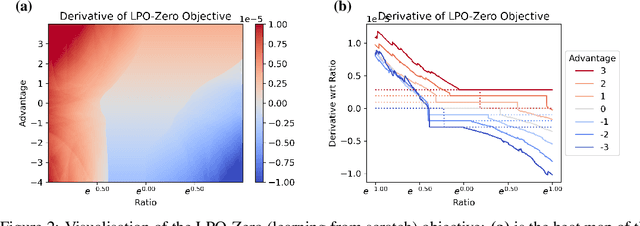

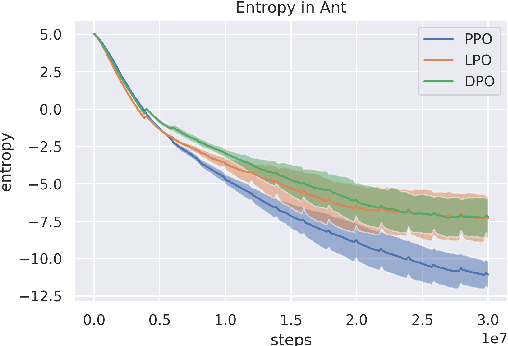
Abstract:Tremendous progress has been made in reinforcement learning (RL) over the past decade. Most of these advancements came through the continual development of new algorithms, which were designed using a combination of mathematical derivations, intuitions, and experimentation. Such an approach of creating algorithms manually is limited by human understanding and ingenuity. In contrast, meta-learning provides a toolkit for automatic machine learning method optimisation, potentially addressing this flaw. However, black-box approaches which attempt to discover RL algorithms with minimal prior structure have thus far not outperformed existing hand-crafted algorithms. Mirror Learning, which includes RL algorithms, such as PPO, offers a potential middle-ground starting point: while every method in this framework comes with theoretical guarantees, components that differentiate them are subject to design. In this paper we explore the Mirror Learning space by meta-learning a "drift" function. We refer to the immediate result as Learnt Policy Optimisation (LPO). By analysing LPO we gain original insights into policy optimisation which we use to formulate a novel, closed-form RL algorithm, Discovered Policy Optimisation (DPO). Our experiments in Brax environments confirm state-of-the-art performance of LPO and DPO, as well as their transfer to unseen settings.
COLA: Consistent Learning with Opponent-Learning Awareness
Mar 08, 2022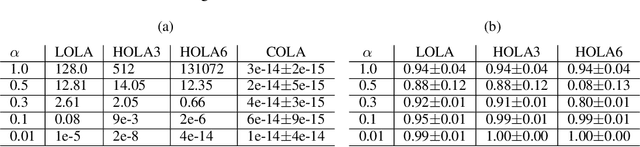
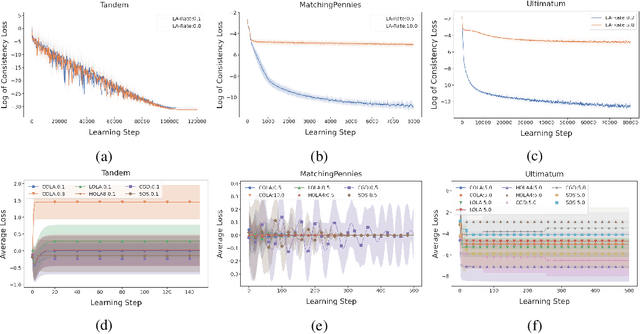
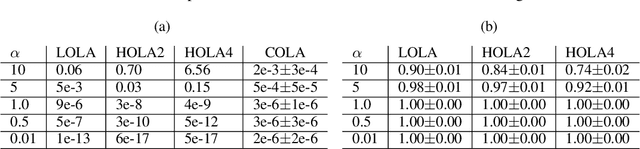
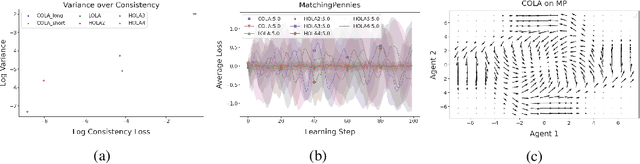
Abstract:Learning in general-sum games can be unstable and often leads to socially undesirable, Pareto-dominated outcomes. To mitigate this, Learning with Opponent-Learning Awareness (LOLA) introduced opponent shaping to this setting, by accounting for the agent's influence on the anticipated learning steps of other agents. However, the original LOLA formulation (and follow-up work) is inconsistent because LOLA models other agents as naive learners rather than LOLA agents. In previous work, this inconsistency was suggested as a cause of LOLA's failure to preserve stable fixed points (SFPs). First, we formalize consistency and show that higher-order LOLA (HOLA) solves LOLA's inconsistency problem if it converges. Second, we correct a claim made in the literature, by proving that, contrary to Sch\"afer and Anandkumar (2019), Competitive Gradient Descent (CGD) does not recover HOLA as a series expansion. Hence, CGD also does not solve the consistency problem. Third, we propose a new method called Consistent LOLA (COLA), which learns update functions that are consistent under mutual opponent shaping. It requires no more than second-order derivatives and learns consistent update functions even when HOLA fails to converge. However, we also prove that even consistent update functions do not preserve SFPs, contradicting the hypothesis that this shortcoming is caused by LOLA's inconsistency. Finally, in an empirical evaluation on a set of general-sum games, we find that COLA finds prosocial solutions and that it converges under a wider range of learning rates than HOLA and LOLA. We support the latter finding with a theoretical result for a simple game.
Polymatrix Competitive Gradient Descent
Nov 16, 2021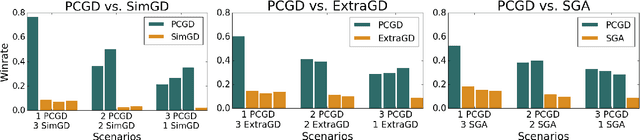
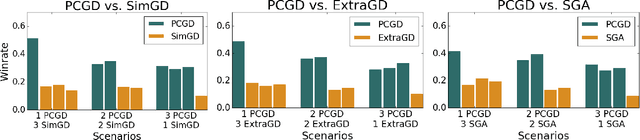


Abstract:Many economic games and machine learning approaches can be cast as competitive optimization problems where multiple agents are minimizing their respective objective function, which depends on all agents' actions. While gradient descent is a reliable basic workhorse for single-agent optimization, it often leads to oscillation in competitive optimization. In this work we propose polymatrix competitive gradient descent (PCGD) as a method for solving general sum competitive optimization involving arbitrary numbers of agents. The updates of our method are obtained as the Nash equilibria of a local polymatrix approximation with a quadratic regularization, and can be computed efficiently by solving a linear system of equations. We prove local convergence of PCGD to stable fixed points for $n$-player general-sum games, and show that it does not require adapting the step size to the strength of the player-interactions. We use PCGD to optimize policies in multi-agent reinforcement learning and demonstrate its advantages in Snake, Markov soccer and an electricity market game. Agents trained by PCGD outperform agents trained with simultaneous gradient descent, symplectic gradient adjustment, and extragradient in Snake and Markov soccer games and on the electricity market game, PCGD trains faster than both simultaneous gradient descent and the extragradient method.
Ridge Rider: Finding Diverse Solutions by Following Eigenvectors of the Hessian
Nov 12, 2020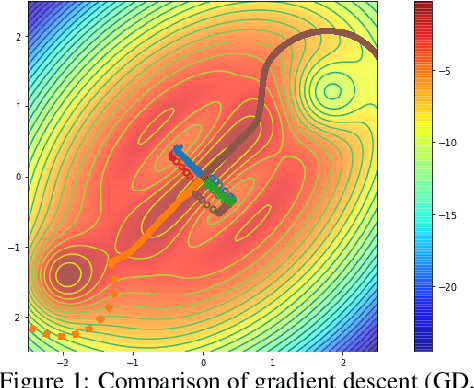
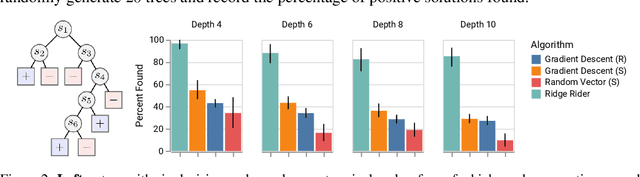
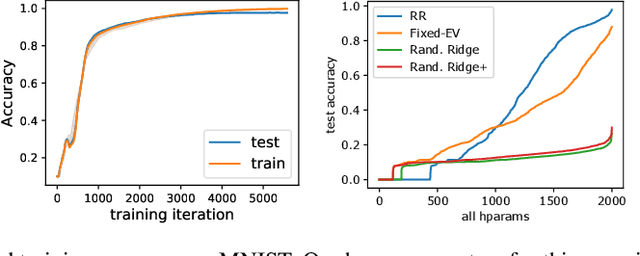
Abstract:Over the last decade, a single algorithm has changed many facets of our lives - Stochastic Gradient Descent (SGD). In the era of ever decreasing loss functions, SGD and its various offspring have become the go-to optimization tool in machine learning and are a key component of the success of deep neural networks (DNNs). While SGD is guaranteed to converge to a local optimum (under loose assumptions), in some cases it may matter which local optimum is found, and this is often context-dependent. Examples frequently arise in machine learning, from shape-versus-texture-features to ensemble methods and zero-shot coordination. In these settings, there are desired solutions which SGD on 'standard' loss functions will not find, since it instead converges to the 'easy' solutions. In this paper, we present a different approach. Rather than following the gradient, which corresponds to a locally greedy direction, we instead follow the eigenvectors of the Hessian, which we call "ridges". By iteratively following and branching amongst the ridges, we effectively span the loss surface to find qualitatively different solutions. We show both theoretically and experimentally that our method, called Ridge Rider (RR), offers a promising direction for a variety of challenging problems.
On the Impossibility of Global Convergence in Multi-Loss Optimization
May 26, 2020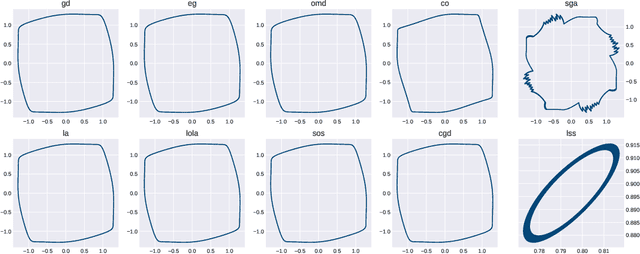

Abstract:Under mild regularity conditions, gradient-based methods converge globally to a critical point in the single-loss setting. This is known to break down for vanilla gradient descent when moving to multi-loss optimization, but can we hope to build some algorithm with global guarantees? We negatively resolve this open problem by proving that any reasonable algorithm will exhibit limit cycles or diverge to infinite losses in some differentiable game, even in two-player games with zero-sum interactions. A reasonable algorithm is simply one which avoids strict maxima, an exceedingly weak assumption since converging to maxima would be the opposite of minimization. This impossibility theorem holds even if we impose existence of a strict minimum and no other critical points. The proof is constructive, enabling us to display explicit limit cycles for existing gradient-based methods. Nonetheless, it remains an open question whether cycles arise in high-dimensional games of interest to ML practitioners, such as GANs or multi-agent RL.
Differentiable Game Mechanics
May 13, 2019
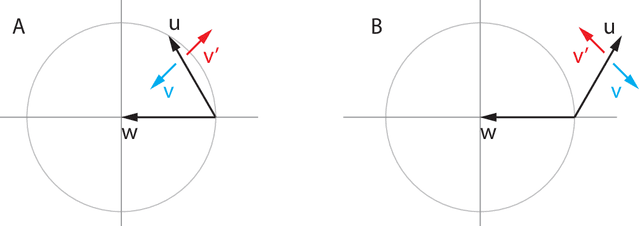
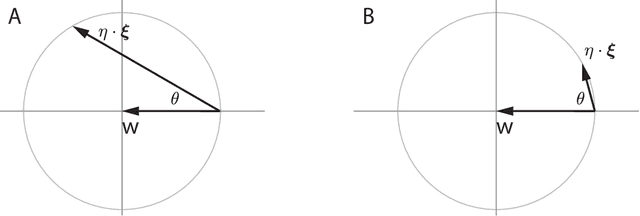
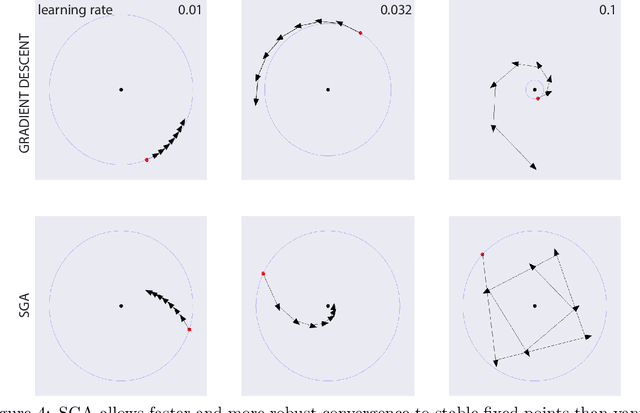
Abstract:Deep learning is built on the foundational guarantee that gradient descent on an objective function converges to local minima. Unfortunately, this guarantee fails in settings, such as generative adversarial nets, that exhibit multiple interacting losses. The behavior of gradient-based methods in games is not well understood -- and is becoming increasingly important as adversarial and multi-objective architectures proliferate. In this paper, we develop new tools to understand and control the dynamics in n-player differentiable games. The key result is to decompose the game Jacobian into two components. The first, symmetric component, is related to potential games, which reduce to gradient descent on an implicit function. The second, antisymmetric component, relates to Hamiltonian games, a new class of games that obey a conservation law akin to conservation laws in classical mechanical systems. The decomposition motivates Symplectic Gradient Adjustment (SGA), a new algorithm for finding stable fixed points in differentiable games. Basic experiments show SGA is competitive with recently proposed algorithms for finding stable fixed points in GANs -- while at the same time being applicable to, and having guarantees in, much more general cases.
* JMLR 2019, journal version of arXiv:1802.05642
Stable Opponent Shaping in Differentiable Games
Nov 20, 2018
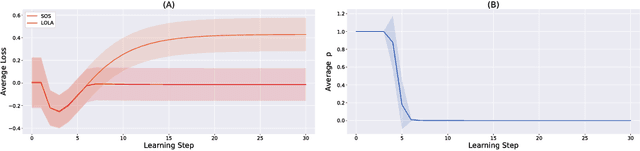
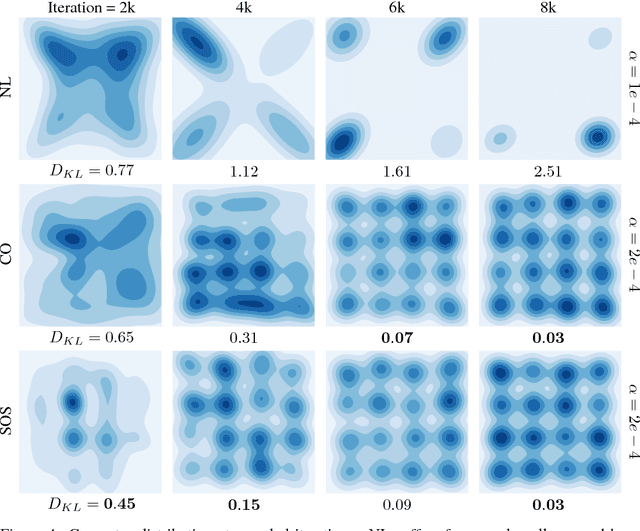

Abstract:A growing number of learning methods are actually \emph{games} which optimise multiple, interdependent objectives in parallel -- from GANs and intrinsic curiosity to multi-agent RL. Opponent shaping is a powerful approach to improve learning dynamics in such games, accounting for the fact that the 'environment' includes agents adapting to one another's updates. Learning with Opponent-Learning Awareness (LOLA) is a recent algorithm which exploits this dynamic response and encourages cooperation in settings like the Iterated Prisoner's Dilemma. Although experimentally successful, we show that LOLA can exhibit 'arrogant' behaviour directly at odds with convergence. In fact, remarkably few algorithms have theoretical guarantees applying across all differentiable games. In this paper we present Stable Opponent Shaping (SOS), a new method that interpolates between LOLA and a stable variant named LookAhead. We prove that LookAhead locally converges and avoids strict saddles in \emph{all differentiable games}, the strongest results in the field so far. SOS inherits these desirable guarantees, while also shaping the learning of opponents and consistently either matching or outperforming LOLA experimentally.
Automatic Conflict Detection in Police Body-Worn Audio
Feb 14, 2018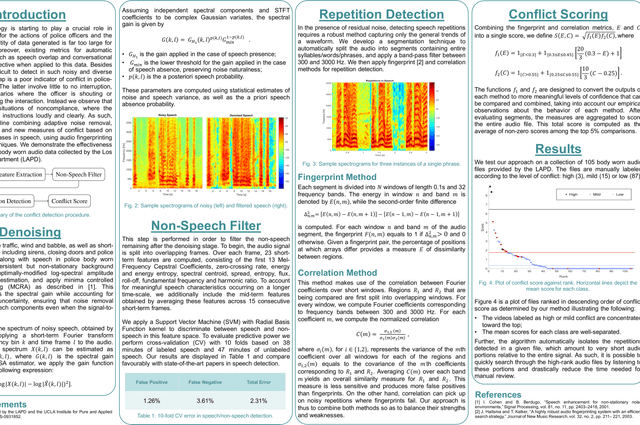
Abstract:Automatic conflict detection has grown in relevance with the advent of body-worn technology, but existing metrics such as turn-taking and overlap are poor indicators of conflict in police-public interactions. Moreover, standard techniques to compute them fall short when applied to such diversified and noisy contexts. We develop a pipeline catered to this task combining adaptive noise removal, non-speech filtering and new measures of conflict based on the repetition and intensity of phrases in speech. We demonstrate the effectiveness of our approach on body-worn audio data collected by the Los Angeles Police Department.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge