A2Perf: Real-World Autonomous Agents Benchmark

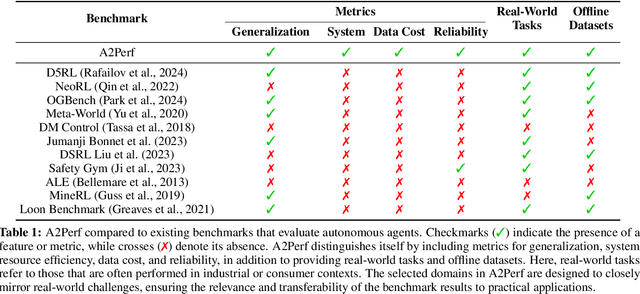
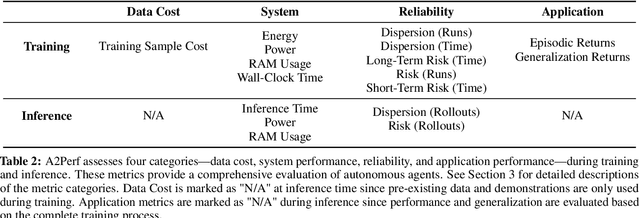
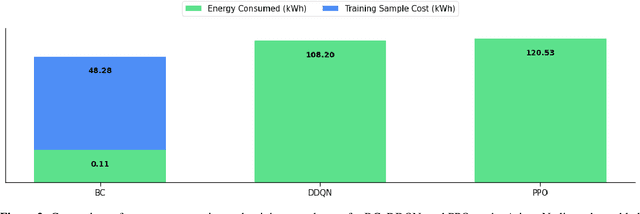
Autonomous agents and systems cover a number of application areas, from robotics and digital assistants to combinatorial optimization, all sharing common, unresolved research challenges. It is not sufficient for agents to merely solve a given task; they must generalize to out-of-distribution tasks, perform reliably, and use hardware resources efficiently during training and inference, among other requirements. Several methods, such as reinforcement learning and imitation learning, are commonly used to tackle these problems, each with different trade-offs. However, there is a lack of benchmarking suites that define the environments, datasets, and metrics which can be used to provide a meaningful way for the community to compare progress on applying these methods to real-world problems. We introduce A2Perf--a benchmark with three environments that closely resemble real-world domains: computer chip floorplanning, web navigation, and quadruped locomotion. A2Perf provides metrics that track task performance, generalization, system resource efficiency, and reliability, which are all critical to real-world applications. Using A2Perf, we demonstrate that web navigation agents can achieve latencies comparable to human reaction times on consumer hardware, reveal reliability trade-offs between algorithms for quadruped locomotion, and quantify the energy costs of different learning approaches for computer chip-design. In addition, we propose a data cost metric to account for the cost incurred acquiring offline data for imitation learning and hybrid algorithms, which allows us to better compare these approaches. A2Perf also contains several standard baselines, enabling apples-to-apples comparisons across methods and facilitating progress in real-world autonomy. As an open-source benchmark, A2Perf is designed to remain accessible, up-to-date, and useful to the research community over the long term.

Understanding Silent Data Corruption in LLM Training

As the scale of training large language models (LLMs) increases, one emergent failure is silent data corruption (SDC), where hardware produces incorrect computations without explicit failure signals. In this work, we are the first to investigate the impact of real-world SDCs on LLM training by comparing model training between healthy production nodes and unhealthy nodes exhibiting SDCs. With the help from a cloud computing platform, we access the unhealthy nodes that were swept out from production by automated fleet management. Using deterministic execution via XLA compiler and our proposed synchronization mechanisms, we isolate and analyze the impact of SDC errors on these nodes at three levels: at each submodule computation, at a single optimizer step, and at a training period. Our results reveal that the impact of SDCs on computation varies on different unhealthy nodes. Although in most cases the perturbations from SDCs on submodule computation and gradients are relatively small, SDCs can lead models to converge to different optima with different weights and even cause spikes in the training loss. Our analysis sheds light on further understanding and mitigating the impact of SDCs.

QuArch: A Question-Answering Dataset for AI Agents in Computer Architecture

We introduce QuArch, a dataset of 1500 human-validated question-answer pairs designed to evaluate and enhance language models' understanding of computer architecture. The dataset covers areas including processor design, memory systems, and performance optimization. Our analysis highlights a significant performance gap: the best closed-source model achieves 84% accuracy, while the top small open-source model reaches 72%. We observe notable struggles in memory systems, interconnection networks, and benchmarking. Fine-tuning with QuArch improves small model accuracy by up to 8%, establishing a foundation for advancing AI-driven computer architecture research. The dataset and leaderboard are at https://harvard-edge.github.io/QuArch/.

FedStaleWeight: Buffered Asynchronous Federated Learning with Fair Aggregation via Staleness Reweighting

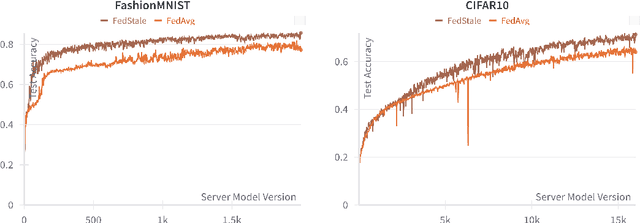
Federated Learning (FL) endeavors to harness decentralized data while preserving privacy, facing challenges of performance, scalability, and collaboration. Asynchronous Federated Learning (AFL) methods have emerged as promising alternatives to their synchronous counterparts bounded by the slowest agent, yet they add additional challenges in convergence guarantees, fairness with respect to compute heterogeneity, and incorporation of staleness in aggregated updates. Specifically, AFL biases model training heavily towards agents who can produce updates faster, leaving slower agents behind, who often also have differently distributed data which is not learned by the global model. Naively upweighting introduces incentive issues, where true fast updating agents may falsely report updates at a slower speed to increase their contribution to model training. We introduce FedStaleWeight, an algorithm addressing fairness in aggregating asynchronous client updates by employing average staleness to compute fair re-weightings. FedStaleWeight reframes asynchronous federated learning aggregation as a mechanism design problem, devising a weighting strategy that incentivizes truthful compute speed reporting without favoring faster update-producing agents by upweighting agent updates based on staleness. Leveraging only observed agent update staleness, FedStaleWeight results in more equitable aggregation on a per-agent basis. We both provide theoretical convergence guarantees in the smooth, non-convex setting and empirically compare FedStaleWeight against the commonly used asynchronous FedBuff with gradient averaging, demonstrating how it achieves stronger fairness, expediting convergence to a higher global model accuracy. Finally, we provide an open-source test bench to facilitate exploration of buffered AFL aggregation strategies, fostering further research in asynchronous federated learning paradigms.

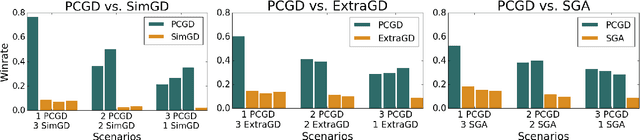
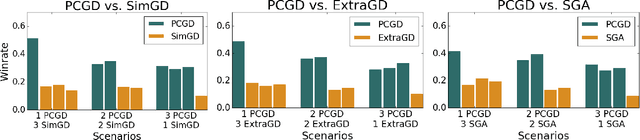
Polymatrix Competitive Gradient Descent

Many economic games and machine learning approaches can be cast as competitive optimization problems where multiple agents are minimizing their respective objective function, which depends on all agents' actions. While gradient descent is a reliable basic workhorse for single-agent optimization, it often leads to oscillation in competitive optimization. In this work we propose polymatrix competitive gradient descent (PCGD) as a method for solving general sum competitive optimization involving arbitrary numbers of agents. The updates of our method are obtained as the Nash equilibria of a local polymatrix approximation with a quadratic regularization, and can be computed efficiently by solving a linear system of equations. We prove local convergence of PCGD to stable fixed points for $n$-player general-sum games, and show that it does not require adapting the step size to the strength of the player-interactions. We use PCGD to optimize policies in multi-agent reinforcement learning and demonstrate its advantages in Snake, Markov soccer and an electricity market game. Agents trained by PCGD outperform agents trained with simultaneous gradient descent, symplectic gradient adjustment, and extragradient in Snake and Markov soccer games and on the electricity market game, PCGD trains faster than both simultaneous gradient descent and the extragradient method.

Diagnostic Image Quality Assessment and Classification in Medical Imaging: Opportunities and Challenges

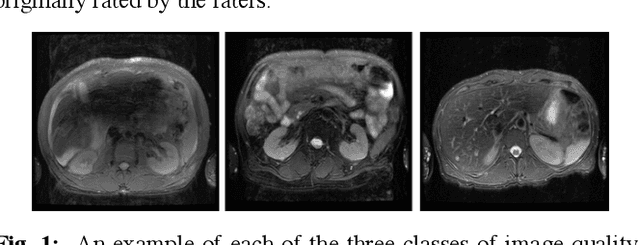
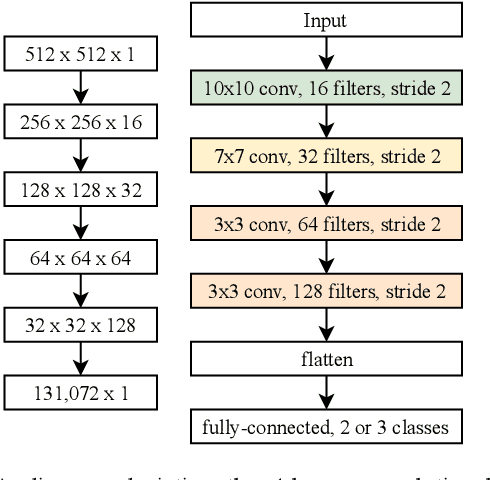
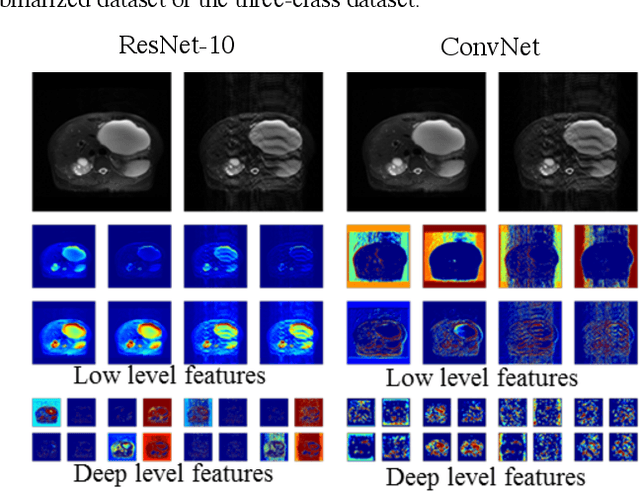
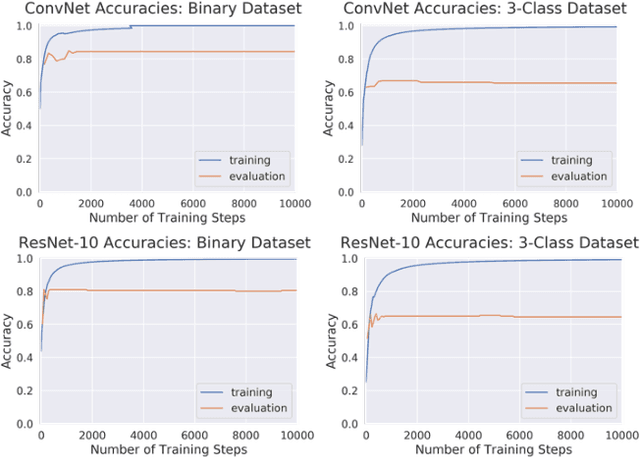
Magnetic Resonance Imaging (MRI) suffers from several artifacts, the most common of which are motion artifacts. These artifacts often yield images that are of non-diagnostic quality. To detect such artifacts, images are prospectively evaluated by experts for their diagnostic quality, which necessitates patient-revisits and rescans whenever non-diagnostic quality scans are encountered. This motivates the need to develop an automated framework capable of accessing medical image quality and detecting diagnostic and non-diagnostic images. In this paper, we explore several convolutional neural network-based frameworks for medical image quality assessment and investigate several challenges therein.