Florian Schäfer
A Bootstrap Perspective on Stochastic Gradient Descent
Dec 08, 2025Abstract:Machine learning models trained with \emph{stochastic} gradient descent (SGD) can generalize better than those trained with deterministic gradient descent (GD). In this work, we study SGD's impact on generalization through the lens of the statistical bootstrap: SGD uses gradient variability under batch sampling as a proxy for solution variability under the randomness of the data collection process. We use empirical results and theoretical analysis to substantiate this claim. In idealized experiments on empirical risk minimization, we show that SGD is drawn to parameter choices that are robust under resampling and thus avoids spurious solutions even if they lie in wider and deeper minima of the training loss. We prove rigorously that by implicitly regularizing the trace of the gradient covariance matrix, SGD controls the algorithmic variability. This regularization leads to solutions that are less sensitive to sampling noise, thereby improving generalization. Numerical experiments on neural network training show that explicitly incorporating the estimate of the algorithmic variability as a regularizer improves test performance. This fact supports our claim that bootstrap estimation underpins SGD's generalization advantages.
InRank: Incremental Low-Rank Learning
Jun 20, 2023



Abstract:The theory of greedy low-rank learning (GLRL) aims to explain the impressive generalization capabilities of deep learning. It proves that stochastic gradient-based training implicitly regularizes neural networks towards low-rank solutions through a gradual increase of the rank during training. However, there is a gap between theory and practice since GLRL requires an infinitesimal initialization of the weights, which is not practical due to the fact that it is a saddle point. In this work, we remove the assumption of infinitesimal initialization by focusing on cumulative weight updates. We prove the cumulative weight updates follow an incremental low-rank trajectory for arbitrary orthogonal initialization of weights in a three-layer linear network. Empirically, we demonstrate that our theory holds on a broad range of neural networks (e.g., transformers) and standard training algorithms (e.g., SGD, Adam). However, existing training algorithms do not exploit the low-rank property to improve computational efficiency as the networks are not parameterized in low-rank. To remedy this, we design a new training algorithm Incremental Low-Rank Learning (InRank), which explicitly expresses cumulative weight updates as low-rank matrices while incrementally augmenting their ranks during training. We evaluate InRank on GPT-2, and our results indicate that InRank achieves comparable prediction performance as the full-rank counterpart while requiring at most 33% of the total ranks throughout training. We also propose an efficient version of InRank that achieves a reduction of 20% in total training time and 37% in memory usage when training GPT-medium on WikiText-103 from scratch.
Sparse Cholesky Factorization for Solving Nonlinear PDEs via Gaussian Processes
Apr 03, 2023Abstract:We study the computational scalability of a Gaussian process (GP) framework for solving general nonlinear partial differential equations (PDEs). This framework transforms solving PDEs to solving quadratic optimization problem with nonlinear constraints. Its complexity bottleneck lies in computing with dense kernel matrices obtained from pointwise evaluations of the covariance kernel of the GP and its partial derivatives at collocation points. We present a sparse Cholesky factorization algorithm for such kernel matrices based on the near-sparsity of the Cholesky factor under a new ordering of Diracs and derivative measurements. We rigorously identify the sparsity pattern and quantify the exponentially convergent accuracy of the corresponding Vecchia approximation of the GP, which is optimal in the Kullback-Leibler divergence. This enables us to compute $\epsilon$-approximate inverse Cholesky factors of the kernel matrices with complexity $O(N\log^d(N/\epsilon))$ in space and $O(N\log^{2d}(N/\epsilon))$ in time. With the sparse factors, gradient-based optimization methods become scalable. Furthermore, we can use the oftentimes more efficient Gauss-Newton method, for which we apply the conjugate gradient algorithm with the sparse factor of a reduced kernel matrix as a preconditioner to solve the linear system. We numerically illustrate our algorithm's near-linear space/time complexity for a broad class of nonlinear PDEs such as the nonlinear elliptic, Burgers, and Monge-Amp\`ere equations. In summary, we provide a fast, scalable, and accurate method for solving general PDEs with GPs.
Competitive Physics Informed Networks
Apr 23, 2022



Abstract:Physics Informed Neural Networks (PINNs) solve partial differential equations (PDEs) by representing them as neural networks. The original PINN implementation does not provide high accuracy, typically attaining about $0.1\%$ relative error. We formulate and test an adversarial approach called competitive PINNs (CPINNs) to overcome this limitation. CPINNs train a discriminator that is rewarded for predicting PINN mistakes. The discriminator and PINN participate in a zero-sum game with the exact PDE solution as an optimal strategy. This approach avoids the issue of squaring the large condition numbers of PDE discretizations. Numerical experiments show that a CPINN trained with competitive gradient descent can achieve errors two orders of magnitude smaller than that of a PINN trained with Adam or stochastic gradient descent.
Polymatrix Competitive Gradient Descent
Nov 16, 2021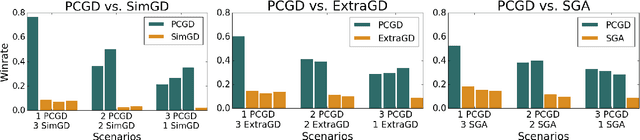
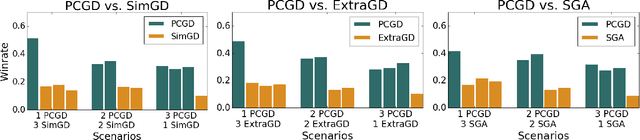


Abstract:Many economic games and machine learning approaches can be cast as competitive optimization problems where multiple agents are minimizing their respective objective function, which depends on all agents' actions. While gradient descent is a reliable basic workhorse for single-agent optimization, it often leads to oscillation in competitive optimization. In this work we propose polymatrix competitive gradient descent (PCGD) as a method for solving general sum competitive optimization involving arbitrary numbers of agents. The updates of our method are obtained as the Nash equilibria of a local polymatrix approximation with a quadratic regularization, and can be computed efficiently by solving a linear system of equations. We prove local convergence of PCGD to stable fixed points for $n$-player general-sum games, and show that it does not require adapting the step size to the strength of the player-interactions. We use PCGD to optimize policies in multi-agent reinforcement learning and demonstrate its advantages in Snake, Markov soccer and an electricity market game. Agents trained by PCGD outperform agents trained with simultaneous gradient descent, symplectic gradient adjustment, and extragradient in Snake and Markov soccer games and on the electricity market game, PCGD trains faster than both simultaneous gradient descent and the extragradient method.
ZerO Initialization: Initializing Residual Networks with only Zeros and Ones
Oct 25, 2021



Abstract:Deep neural networks are usually initialized with random weights, with adequately selected initial variance to ensure stable signal propagation during training. However, there is no consensus on how to select the variance, and this becomes challenging especially as the number of layers grows. In this work, we replace the widely used random weight initialization with a fully deterministic initialization scheme ZerO, which initializes residual networks with only zeros and ones. By augmenting the standard ResNet architectures with a few extra skip connections and Hadamard transforms, ZerO allows us to start the training from zeros and ones entirely. This has many benefits such as improving reproducibility (by reducing the variance over different experimental runs) and allowing network training without batch normalization. Surprisingly, we find that ZerO achieves state-of-the-art performance over various image classification datasets, including ImageNet, which suggests random weights may be unnecessary for modern network initialization.
Competitive Mirror Descent
Jun 17, 2020



Abstract:Constrained competitive optimization involves multiple agents trying to minimize conflicting objectives, subject to constraints. This is a highly expressive modeling language that subsumes most of modern machine learning. In this work we propose competitive mirror descent (CMD): a general method for solving such problems based on first order information that can be obtained by automatic differentiation. First, by adding Lagrange multipliers, we obtain a simplified constraint set with an associated Bregman potential. At each iteration, we then solve for the Nash equilibrium of a regularized bilinear approximation of the full problem to obtain a direction of movement of the agents. Finally, we obtain the next iterate by following this direction according to the dual geometry induced by the Bregman potential. By using the dual geometry we obtain feasible iterates despite only solving a linear system at each iteration, eliminating the need for projection steps while still accounting for the global nonlinear structure of the constraint set. As a special case we obtain a novel competitive multiplicative weights algorithm for problems on the positive cone.
Implicit competitive regularization in GANs
Oct 13, 2019



Abstract:Generative adversarial networks (GANs) are capable of producing high quality samples, but they suffer from numerous issues such as instability and mode collapse during training. To combat this, we propose to model the generator and discriminator as agents acting under local information, uncertainty, and awareness of their opponent. By doing so we achieve stable convergence, even when the underlying game has no Nash equilibria. We call this mechanism implicit competitive regularization (ICR) and show that it is present in the recently proposed competitive gradient descent (CGD). When comparing CGD to Adam using a variety of loss functions and regularizers on CIFAR10, CGD shows a much more consistent performance, which we attribute to ICR. In our experiments, we achieve the highest inception score when using the WGAN loss (without gradient penalty or weight clipping) together with CGD. This can be interpreted as minimizing a form of integral probability metric based on ICR.
Competitive Gradient Descent
May 28, 2019



Abstract:We introduce a new algorithm for the numerical computation of Nash equilibria of competitive two-player games. Our method is a natural generalization of gradient descent to the two-player setting where the update is given by the Nash equilibrium of a regularized bilinear local approximation of the underlying game. It avoids oscillatory and divergent behaviors seen in alternating gradient descent. Using numerical experiments and rigorous analysis, we provide a detailed comparison to methods based on \emph{optimism} and \emph{consensus} and show that our method avoids making any unnecessary changes to the gradient dynamics while achieving exponential (local) convergence for (locally) convex-concave zero sum games. Convergence and stability properties of our method are robust to strong interactions between the players, without adapting the stepsize, which is not the case with previous methods. In our numerical experiments on non-convex-concave problems, existing methods are prone to divergence and instability due to their sensitivity to interactions among the players, whereas we never observe divergence of our algorithm. The ability to choose larger stepsizes furthermore allows our algorithm to achieve faster convergence, as measured by the number of model evaluations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge