Advancing End-to-End Pixel Space Generative Modeling via Self-supervised Pre-training

Pixel-space generative models are often more difficult to train and generally underperform compared to their latent-space counterparts, leaving a persistent performance and efficiency gap. In this paper, we introduce a novel two-stage training framework that closes this gap for pixel-space diffusion and consistency models. In the first stage, we pre-train encoders to capture meaningful semantics from clean images while aligning them with points along the same deterministic sampling trajectory, which evolves points from the prior to the data distribution. In the second stage, we integrate the encoder with a randomly initialized decoder and fine-tune the complete model end-to-end for both diffusion and consistency models. Our training framework demonstrates strong empirical performance on ImageNet dataset. Specifically, our diffusion model reaches an FID of 2.04 on ImageNet-256 and 2.35 on ImageNet-512 with 75 number of function evaluations (NFE), surpassing prior pixel-space methods by a large margin in both generation quality and efficiency while rivaling leading VAE-based models at comparable training cost. Furthermore, on ImageNet-256, our consistency model achieves an impressive FID of 8.82 in a single sampling step, significantly surpassing its latent-space counterpart. To the best of our knowledge, this marks the first successful training of a consistency model directly on high-resolution images without relying on pre-trained VAEs or diffusion models.

InverseBench: Benchmarking Plug-and-Play Diffusion Priors for Inverse Problems in Physical Sciences

Plug-and-play diffusion priors (PnPDP) have emerged as a promising research direction for solving inverse problems. However, current studies primarily focus on natural image restoration, leaving the performance of these algorithms in scientific inverse problems largely unexplored. To address this gap, we introduce \textsc{InverseBench}, a framework that evaluates diffusion models across five distinct scientific inverse problems. These problems present unique structural challenges that differ from existing benchmarks, arising from critical scientific applications such as optical tomography, medical imaging, black hole imaging, seismology, and fluid dynamics. With \textsc{InverseBench}, we benchmark 14 inverse problem algorithms that use plug-and-play diffusion priors against strong, domain-specific baselines, offering valuable new insights into the strengths and weaknesses of existing algorithms. To facilitate further research and development, we open-source the codebase, along with datasets and pre-trained models, at https://devzhk.github.io/InverseBench/.

Ensemble Kalman Diffusion Guidance: A Derivative-free Method for Inverse Problems

When solving inverse problems, it is increasingly popular to use pre-trained diffusion models as plug-and-play priors. This framework can accommodate different forward models without re-training while preserving the generative capability of diffusion models. Despite their success in many imaging inverse problems, most existing methods rely on privileged information such as derivative, pseudo-inverse, or full knowledge about the forward model. This reliance poses a substantial limitation that restricts their use in a wide range of problems where such information is unavailable, such as in many scientific applications. To address this issue, we propose Ensemble Kalman Diffusion Guidance (EnKG) for diffusion models, a derivative-free approach that can solve inverse problems by only accessing forward model evaluations and a pre-trained diffusion model prior. We study the empirical effectiveness of our method across various inverse problems, including scientific settings such as inferring fluid flows and astronomical objects, which are highly non-linear inverse problems that often only permit black-box access to the forward model.

Fast Training of Diffusion Models with Masked Transformers

We propose an efficient approach to train large diffusion models with masked transformers. While masked transformers have been extensively explored for representation learning, their application to generative learning is less explored in the vision domain. Our work is the first to exploit masked training to reduce the training cost of diffusion models significantly. Specifically, we randomly mask out a high proportion (\emph{e.g.}, 50\%) of patches in diffused input images during training. For masked training, we introduce an asymmetric encoder-decoder architecture consisting of a transformer encoder that operates only on unmasked patches and a lightweight transformer decoder on full patches. To promote a long-range understanding of full patches, we add an auxiliary task of reconstructing masked patches to the denoising score matching objective that learns the score of unmasked patches. Experiments on ImageNet-256$\times$256 show that our approach achieves the same performance as the state-of-the-art Diffusion Transformer (DiT) model, using only 31\% of its original training time. Thus, our method allows for efficient training of diffusion models without sacrificing the generative performance.

Fast Sampling of Diffusion Models via Operator Learning

Diffusion models have found widespread adoption in various areas. However, sampling from them is slow because it involves emulating a reverse process with hundreds-to-thousands of network evaluations. Inspired by the success of neural operators in accelerating differential equations solving, we approach this problem by solving the underlying neural differential equation from an operator learning perspective. We examine probability flow ODE trajectories in diffusion models and observe a compact energy spectrum that can be learned efficiently in Fourier space. With this insight, we propose diffusion Fourier neural operator (DFNO) with temporal convolution in Fourier space to parameterize the operator that maps initial condition to the solution trajectory, which is a continuous function in time. DFNO can be applied to any diffusion model and generate high-quality samples in one model forward call. Our method achieves the state-of-the-art FID of 4.72 on CIFAR-10 using only one model evaluation.

Langevin Monte Carlo for Contextual Bandits

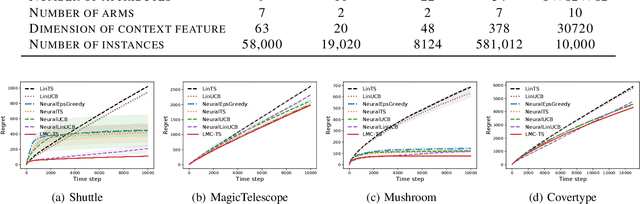
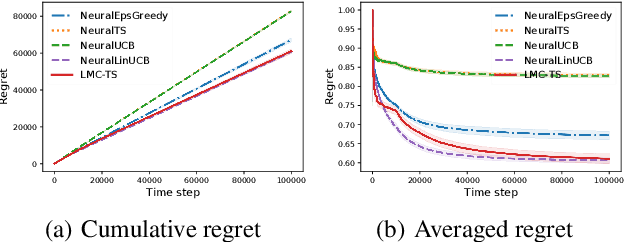
We study the efficiency of Thompson sampling for contextual bandits. Existing Thompson sampling-based algorithms need to construct a Laplace approximation (i.e., a Gaussian distribution) of the posterior distribution, which is inefficient to sample in high dimensional applications for general covariance matrices. Moreover, the Gaussian approximation may not be a good surrogate for the posterior distribution for general reward generating functions. We propose an efficient posterior sampling algorithm, viz., Langevin Monte Carlo Thompson Sampling (LMC-TS), that uses Markov Chain Monte Carlo (MCMC) methods to directly sample from the posterior distribution in contextual bandits. Our method is computationally efficient since it only needs to perform noisy gradient descent updates without constructing the Laplace approximation of the posterior distribution. We prove that the proposed algorithm achieves the same sublinear regret bound as the best Thompson sampling algorithms for a special case of contextual bandits, viz., linear contextual bandits. We conduct experiments on both synthetic data and real-world datasets on different contextual bandit models, which demonstrates that directly sampling from the posterior is both computationally efficient and competitive in performance.

Physics-Informed Neural Operator for Learning Partial Differential Equations

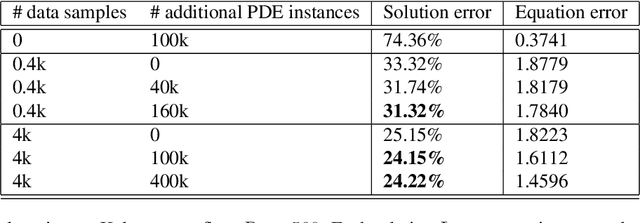
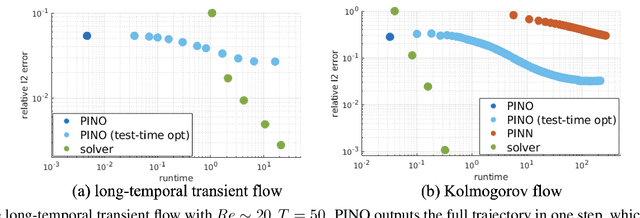
Machine learning methods have recently shown promise in solving partial differential equations (PDEs). They can be classified into two broad categories: approximating the solution function and learning the solution operator. The Physics-Informed Neural Network (PINN) is an example of the former while the Fourier neural operator (FNO) is an example of the latter. Both these approaches have shortcomings. The optimization in PINN is challenging and prone to failure, especially on multi-scale dynamic systems. FNO does not suffer from this optimization issue since it carries out supervised learning on a given dataset, but obtaining such data may be too expensive or infeasible. In this work, we propose the physics-informed neural operator (PINO), where we combine the operating-learning and function-optimization frameworks. This integrated approach improves convergence rates and accuracy over both PINN and FNO models. In the operator-learning phase, PINO learns the solution operator over multiple instances of the parametric PDE family. In the test-time optimization phase, PINO optimizes the pre-trained operator ansatz for the querying instance of the PDE. Experiments show PINO outperforms previous ML methods on many popular PDE families while retaining the extraordinary speed-up of FNO compared to solvers. In particular, PINO accurately solves challenging long temporal transient flows and Kolmogorov flows where other baseline ML methods fail to converge.

Implicit competitive regularization in GANs

Generative adversarial networks (GANs) are capable of producing high quality samples, but they suffer from numerous issues such as instability and mode collapse during training. To combat this, we propose to model the generator and discriminator as agents acting under local information, uncertainty, and awareness of their opponent. By doing so we achieve stable convergence, even when the underlying game has no Nash equilibria. We call this mechanism implicit competitive regularization (ICR) and show that it is present in the recently proposed competitive gradient descent (CGD). When comparing CGD to Adam using a variety of loss functions and regularizers on CIFAR10, CGD shows a much more consistent performance, which we attribute to ICR. In our experiments, we achieve the highest inception score when using the WGAN loss (without gradient penalty or weight clipping) together with CGD. This can be interpreted as minimizing a form of integral probability metric based on ICR.