Good News for Script Kiddies? Evaluating Large Language Models for Automated Exploit Generation

Large Language Models (LLMs) have demonstrated remarkable capabilities in code-related tasks, raising concerns about their potential for automated exploit generation (AEG). This paper presents the first systematic study on LLMs' effectiveness in AEG, evaluating both their cooperativeness and technical proficiency. To mitigate dataset bias, we introduce a benchmark with refactored versions of five software security labs. Additionally, we design an LLM-based attacker to systematically prompt LLMs for exploit generation. Our experiments reveal that GPT-4 and GPT-4o exhibit high cooperativeness, comparable to uncensored models, while Llama3 is the most resistant. However, no model successfully generates exploits for refactored labs, though GPT-4o's minimal errors highlight the potential for LLM-driven AEG advancements.

CRISP: Object Pose and Shape Estimation with Test-Time Adaptation

We consider the problem of estimating object pose and shape from an RGB-D image. Our first contribution is to introduce CRISP, a category-agnostic object pose and shape estimation pipeline. The pipeline implements an encoder-decoder model for shape estimation. It uses FiLM-conditioning for implicit shape reconstruction and a DPT-based network for estimating pose-normalized points for pose estimation. As a second contribution, we propose an optimization-based pose and shape corrector that can correct estimation errors caused by a domain gap. Observing that the shape decoder is well behaved in the convex hull of known shapes, we approximate the shape decoder with an active shape model, and show that this reduces the shape correction problem to a constrained linear least squares problem, which can be solved efficiently by an interior point algorithm. Third, we introduce a self-training pipeline to perform self-supervised domain adaptation of CRISP. The self-training is based on a correct-and-certify approach, which leverages the corrector to generate pseudo-labels at test time, and uses them to self-train CRISP. We demonstrate CRISP (and the self-training) on YCBV, SPE3R, and NOCS datasets. CRISP shows high performance on all the datasets. Moreover, our self-training is capable of bridging a large domain gap. Finally, CRISP also shows an ability to generalize to unseen objects. Code and pre-trained models will be available on https://web.mit.edu/sparklab/research/crisp_object_pose_shape/.

Theoretical Analysis for Expectation-Maximization-Based Multi-Model 3D Registration

We perform detailed theoretical analysis of an expectation-maximization-based algorithm recently proposed in for solving a variation of the 3D registration problem, named multi-model 3D registration. Despite having shown superior empirical results, did not theoretically justify the conditions under which the EM approach converges to the ground truth. In this project, we aim to close this gap by establishing such conditions. In particular, the analysis revolves around the usage of probabilistic tail bounds that are developed and applied in various instances throughout the course. The problem studied in this project stands as another example, different from those seen in the course, in which tail-bounds help advance our algorithmic understanding in a probabilistic way. We provide self-contained background materials on 3D Registration

GMKF: Generalized Moment Kalman Filter for Polynomial Systems with Arbitrary Noise

This paper develops a new filtering approach for state estimation in polynomial systems corrupted by arbitrary noise, which commonly arise in robotics. We first consider a batch setup where we perform state estimation using all data collected from the initial to the current time. We formulate the batch state estimation problem as a Polynomial Optimization Problem (POP) and relax the assumption of Gaussian noise by specifying a finite number of moments of the noise. We solve the resulting POP using a moment relaxation and prove that under suitable conditions on the rank of the relaxation, (i) we can extract a provably optimal estimate from the moment relaxation, and (ii) we can obtain a belief representation from the dual (sum-of-squares) relaxation. We then turn our attention to the filtering setup and apply similar insights to develop a GMKF for recursive state estimation in polynomial systems with arbitrary noise. The GMKF formulates the prediction and update steps as POPs and solves them using moment relaxations, carrying over a possibly non-Gaussian belief. In the linear-Gaussian case, GMKF reduces to the standard Kalman Filter. We demonstrate that GMKF performs well under highly non-Gaussian noise and outperforms common alternatives, including the Extended and Unscented Kalman Filter, and their variants on matrix Lie group.

Multi-Model 3D Registration: Finding Multiple Moving Objects in Cluttered Point Clouds

We investigate a variation of the 3D registration problem, named multi-model 3D registration. In the multi-model registration problem, we are given two point clouds picturing a set of objects at different poses (and possibly including points belonging to the background) and we want to simultaneously reconstruct how all objects moved between the two point clouds. This setup generalizes standard 3D registration where one wants to reconstruct a single pose, e.g., the motion of the sensor picturing a static scene. Moreover, it provides a mathematically grounded formulation for relevant robotics applications, e.g., where a depth sensor onboard a robot perceives a dynamic scene and has the goal of estimating its own motion (from the static portion of the scene) while simultaneously recovering the motion of all dynamic objects. We assume a correspondence-based setup where we have putative matches between the two point clouds and consider the practical case where these correspondences are plagued with outliers. We then propose a simple approach based on Expectation-Maximization (EM) and establish theoretical conditions under which the EM approach converges to the ground truth. We evaluate the approach in simulated and real datasets ranging from table-top scenes to self-driving scenarios and demonstrate its effectiveness when combined with state-of-the-art scene flow methods to establish dense correspondences.

A Design Toolbox for the Development of Collaborative Distributed Machine Learning Systems

To leverage data for the sufficient training of machine learning (ML) models from multiple parties in a confidentiality-preserving way, various collaborative distributed ML (CDML) system designs have been developed, for example, to perform assisted learning, federated learning, and split learning. CDML system designs show different traits, including high agent autonomy, ML model confidentiality, and fault tolerance. Facing a wide variety of CDML system designs with different traits, it is difficult for developers to design CDML systems with traits that match use case requirements in a targeted way. However, inappropriate CDML system designs may result in CDML systems failing their envisioned purposes. We developed a CDML design toolbox that can guide the development of CDML systems. Based on the CDML design toolbox, we present CDML system archetypes with distinct key traits that can support the design of CDML systems to meet use case requirements.

Fusion-in-T5: Unifying Document Ranking Signals for Improved Information Retrieval

Common IR pipelines are typically cascade systems that may involve multiple rankers and/or fusion models to integrate different information step-by-step. In this paper, we propose a novel re-ranker named Fusion-in-T5 (FiT5), which integrates document text information, retrieval features, and global document information into a single unified model using templated-based input and global attention. Experiments on passage ranking benchmarks MS MARCO and TREC DL show that FiT5 significantly improves ranking performance over prior pipelines. Analyses find that through global attention, FiT5 is able to jointly utilize the ranking features via gradually attending to related documents, and thus improve the detection of subtle nuances between them. Our code will be open-sourced.

Physics-Informed Neural Operator for Learning Partial Differential Equations

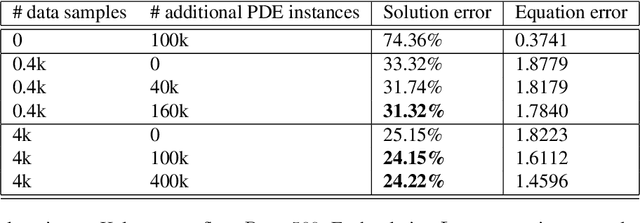
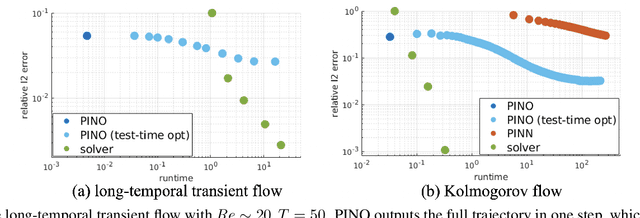
Machine learning methods have recently shown promise in solving partial differential equations (PDEs). They can be classified into two broad categories: approximating the solution function and learning the solution operator. The Physics-Informed Neural Network (PINN) is an example of the former while the Fourier neural operator (FNO) is an example of the latter. Both these approaches have shortcomings. The optimization in PINN is challenging and prone to failure, especially on multi-scale dynamic systems. FNO does not suffer from this optimization issue since it carries out supervised learning on a given dataset, but obtaining such data may be too expensive or infeasible. In this work, we propose the physics-informed neural operator (PINO), where we combine the operating-learning and function-optimization frameworks. This integrated approach improves convergence rates and accuracy over both PINN and FNO models. In the operator-learning phase, PINO learns the solution operator over multiple instances of the parametric PDE family. In the test-time optimization phase, PINO optimizes the pre-trained operator ansatz for the querying instance of the PDE. Experiments show PINO outperforms previous ML methods on many popular PDE families while retaining the extraordinary speed-up of FNO compared to solvers. In particular, PINO accurately solves challenging long temporal transient flows and Kolmogorov flows where other baseline ML methods fail to converge.