Demystifying Data-Driven Probabilistic Medium-Range Weather Forecasting

The recent revolution in data-driven methods for weather forecasting has lead to a fragmented landscape of complex, bespoke architectures and training strategies, obscuring the fundamental drivers of forecast accuracy. Here, we demonstrate that state-of-the-art probabilistic skill requires neither intricate architectural constraints nor specialized training heuristics. We introduce a scalable framework for learning multi-scale atmospheric dynamics by combining a directly downsampled latent space with a history-conditioned local projector that resolves high-resolution physics. We find that our framework design is robust to the choice of probabilistic estimator, seamlessly supporting stochastic interpolants, diffusion models, and CRPS-based ensemble training. Validated against the Integrated Forecasting System and the deep learning probabilistic model GenCast, our framework achieves statistically significant improvements on most of the variables. These results suggest scaling a general-purpose model is sufficient for state-of-the-art medium-range prediction, eliminating the need for tailored training recipes and proving effective across the full spectrum of probabilistic frameworks.

Derivative-Informed Fourier Neural Operator: Universal Approximation and Applications to PDE-Constrained Optimization

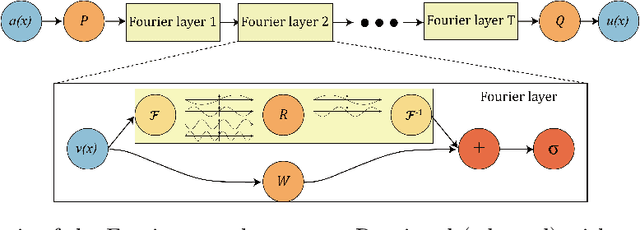
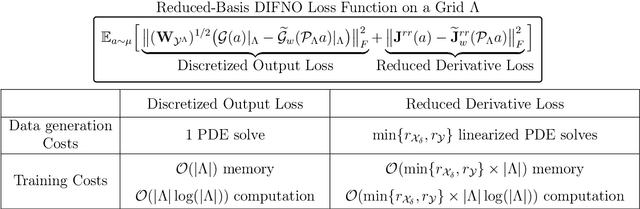
We present approximation theories and efficient training methods for derivative-informed Fourier neural operators (DIFNOs) with applications to PDE-constrained optimization. A DIFNO is an FNO trained by minimizing its prediction error jointly on output and Fréchet derivative samples of a high-fidelity operator (e.g., a parametric PDE solution operator). As a result, a DIFNO can closely emulate not only the high-fidelity operator's response but also its sensitivities. To motivate the use of DIFNOs instead of conventional FNOs as surrogate models, we show that accurate surrogate-driven PDE-constrained optimization requires accurate surrogate Fréchet derivatives. Then, for continuously differentiable operators, we establish (i) simultaneous universal approximation of FNOs and their Fréchet derivatives on compact sets, and (ii) universal approximation of FNOs in weighted Sobolev spaces with input measures that have unbounded supports. Our theoretical results certify the capability of FNOs for accurate derivative-informed operator learning and accurate solution of PDE-constrained optimization. Furthermore, we develop efficient training schemes using dimension reduction and multi-resolution techniques that significantly reduce memory and computational costs for Fréchet derivative learning. Numerical examples on nonlinear diffusion--reaction, Helmholtz, and Navier--Stokes equations demonstrate that DIFNOs are superior in sample complexity for operator learning and solving infinite-dimensional PDE-constrained inverse problems, achieving high accuracy at low training sample sizes.

Geometric Operator Learning with Optimal Transport

We propose integrating optimal transport (OT) into operator learning for partial differential equations (PDEs) on complex geometries. Classical geometric learning methods typically represent domains as meshes, graphs, or point clouds. Our approach generalizes discretized meshes to mesh density functions, formulating geometry embedding as an OT problem that maps these functions to a uniform density in a reference space. Compared to previous methods relying on interpolation or shared deformation, our OT-based method employs instance-dependent deformation, offering enhanced flexibility and effectiveness. For 3D simulations focused on surfaces, our OT-based neural operator embeds the surface geometry into a 2D parameterized latent space. By performing computations directly on this 2D representation of the surface manifold, it achieves significant computational efficiency gains compared to volumetric simulation. Experiments with Reynolds-averaged Navier-Stokes equations (RANS) on the ShapeNet-Car and DrivAerNet-Car datasets show that our method achieves better accuracy and also reduces computational expenses in terms of both time and memory usage compared to existing machine learning models. Additionally, our model demonstrates significantly improved accuracy on the FlowBench dataset, underscoring the benefits of employing instance-dependent deformation for datasets with highly variable geometries.

A Learning-based Domain Decomposition Method

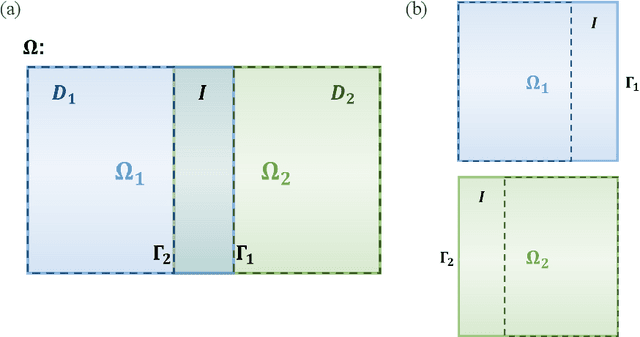
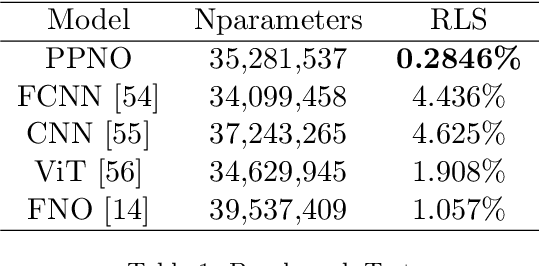
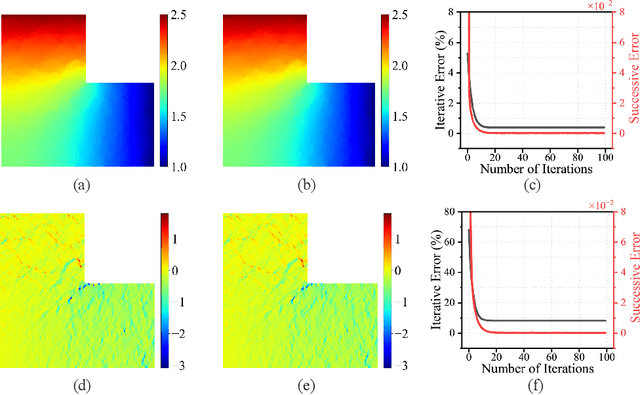
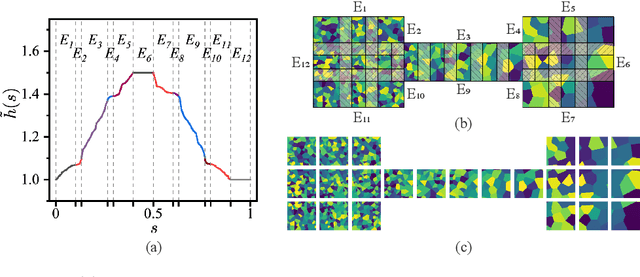
Recent developments in mechanical, aerospace, and structural engineering have driven a growing need for efficient ways to model and analyse structures at much larger and more complex scales than before. While established numerical methods like the Finite Element Method remain reliable, they often struggle with computational cost and scalability when dealing with large and geometrically intricate problems. In recent years, neural network-based methods have shown promise because of their ability to efficiently approximate nonlinear mappings. However, most existing neural approaches are still largely limited to simple domains, which makes it difficult to apply to real-world PDEs involving complex geometries. In this paper, we propose a learning-based domain decomposition method (L-DDM) that addresses this gap. Our approach uses a single, pre-trained neural operator-originally trained on simple domains-as a surrogate model within a domain decomposition scheme, allowing us to tackle large and complicated domains efficiently. We provide a general theoretical result on the existence of neural operator approximations in the context of domain decomposition solution of abstract PDEs. We then demonstrate our method by accurately approximating solutions to elliptic PDEs with discontinuous microstructures in complex geometries, using a physics-pretrained neural operator (PPNO). Our results show that this approach not only outperforms current state-of-the-art methods on these challenging problems, but also offers resolution-invariance and strong generalization to microstructural patterns unseen during training.

InverseBench: Benchmarking Plug-and-Play Diffusion Priors for Inverse Problems in Physical Sciences

Plug-and-play diffusion priors (PnPDP) have emerged as a promising research direction for solving inverse problems. However, current studies primarily focus on natural image restoration, leaving the performance of these algorithms in scientific inverse problems largely unexplored. To address this gap, we introduce \textsc{InverseBench}, a framework that evaluates diffusion models across five distinct scientific inverse problems. These problems present unique structural challenges that differ from existing benchmarks, arising from critical scientific applications such as optical tomography, medical imaging, black hole imaging, seismology, and fluid dynamics. With \textsc{InverseBench}, we benchmark 14 inverse problem algorithms that use plug-and-play diffusion priors against strong, domain-specific baselines, offering valuable new insights into the strengths and weaknesses of existing algorithms. To facilitate further research and development, we open-source the codebase, along with datasets and pre-trained models, at https://devzhk.github.io/InverseBench/.

A Library for Learning Neural Operators

We present NeuralOperator, an open-source Python library for operator learning. Neural operators generalize neural networks to maps between function spaces instead of finite-dimensional Euclidean spaces. They can be trained and inferenced on input and output functions given at various discretizations, satisfying a discretization convergence properties. Built on top of PyTorch, NeuralOperator provides all the tools for training and deploying neural operator models, as well as developing new ones, in a high-quality, tested, open-source package. It combines cutting-edge models and customizability with a gentle learning curve and simple user interface for newcomers.

Ensemble Kalman Diffusion Guidance: A Derivative-free Method for Inverse Problems

When solving inverse problems, it is increasingly popular to use pre-trained diffusion models as plug-and-play priors. This framework can accommodate different forward models without re-training while preserving the generative capability of diffusion models. Despite their success in many imaging inverse problems, most existing methods rely on privileged information such as derivative, pseudo-inverse, or full knowledge about the forward model. This reliance poses a substantial limitation that restricts their use in a wide range of problems where such information is unavailable, such as in many scientific applications. To address this issue, we propose Ensemble Kalman Diffusion Guidance (EnKG) for diffusion models, a derivative-free approach that can solve inverse problems by only accessing forward model evaluations and a pre-trained diffusion model prior. We study the empirical effectiveness of our method across various inverse problems, including scientific settings such as inferring fluid flows and astronomical objects, which are highly non-linear inverse problems that often only permit black-box access to the forward model.

Multi-Grid Tensorized Fourier Neural Operator for High-Resolution PDEs

Memory complexity and data scarcity have so far prohibited learning solution operators of partial differential equations (PDEs) at high resolutions. We address these limitations by introducing a new data efficient and highly parallelizable operator learning approach with reduced memory requirement and better generalization, called multi-grid tensorized neural operator (MG-TFNO). MG-TFNO scales to large resolutions by leveraging local and global structures of full-scale, real-world phenomena, through a decomposition of both the input domain and the operator's parameter space. Our contributions are threefold: i) we enable parallelization over input samples with a novel multi-grid-based domain decomposition, ii) we represent the parameters of the model in a high-order latent subspace of the Fourier domain, through a global tensor factorization, resulting in an extreme reduction in the number of parameters and improved generalization, and iii) we propose architectural improvements to the backbone FNO. Our approach can be used in any operator learning setting. We demonstrate superior performance on the turbulent Navier-Stokes equations where we achieve less than half the error with over 150x compression. The tensorization combined with the domain decomposition, yields over 150x reduction in the number of parameters and 7x reduction in the domain size without losses in accuracy, while slightly enabling parallelism.

Neural Operators for Accelerating Scientific Simulations and Design

Scientific discovery and engineering design are currently limited by the time and cost of physical experiments, selected mostly through trial-and-error and intuition that require deep domain expertise. Numerical simulations present an alternative to physical experiments, but are usually infeasible for complex real-world domains due to the computational requirements of existing numerical methods. Artificial intelligence (AI) presents a potential paradigm shift through the development of fast data-driven surrogate models. In particular, an AI framework, known as neural operators, presents a principled framework for learning mappings between functions defined on continuous domains, e.g., spatiotemporal processes and partial differential equations (PDE). They can extrapolate and predict solutions at new locations unseen during training, i.e., perform zero-shot super-resolution. Neural operators can augment or even replace existing simulators in many applications, such as computational fluid dynamics, weather forecasting, and material modeling, while being 4-5 orders of magnitude faster. Further, neural operators can be integrated with physics and other domain constraints enforced at finer resolutions to obtain high-fidelity solutions and good generalization. Since neural operators are differentiable, they can directly optimize parameters for inverse design and other inverse problems. We believe that neural operators present a transformative approach to simulation and design, enabling rapid research and development.

Tipping Point Forecasting in Non-Stationary Dynamics on Function Spaces

Tipping points are abrupt, drastic, and often irreversible changes in the evolution of non-stationary and chaotic dynamical systems. For instance, increased greenhouse gas concentrations are predicted to lead to drastic decreases in low cloud cover, referred to as a climatological tipping point. In this paper, we learn the evolution of such non-stationary dynamical systems using a novel recurrent neural operator (RNO), which learns mappings between function spaces. After training RNO on only the pre-tipping dynamics, we employ it to detect future tipping points using an uncertainty-based approach. In particular, we propose a conformal prediction framework to forecast tipping points by monitoring deviations from physics constraints (such as conserved quantities and partial differential equations), enabling forecasting of these abrupt changes along with a rigorous measure of uncertainty. We illustrate our proposed methodology on non-stationary ordinary and partial differential equations, such as the Lorenz-63 and Kuramoto-Sivashinsky equations. We also apply our methods to forecast a climate tipping point in stratocumulus cloud cover. In our experiments, we demonstrate that even partial or approximate physics constraints can be used to accurately forecast future tipping points.