Jean Kossaifi
NEUROSPIN, LTCI
Analyzing Political Text at Scale with Online Tensor LDA
Nov 11, 2025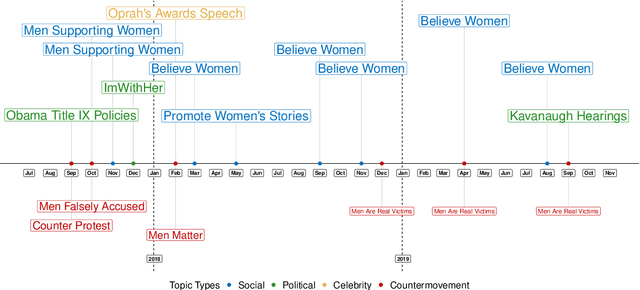

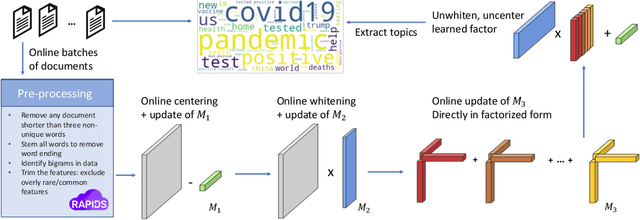
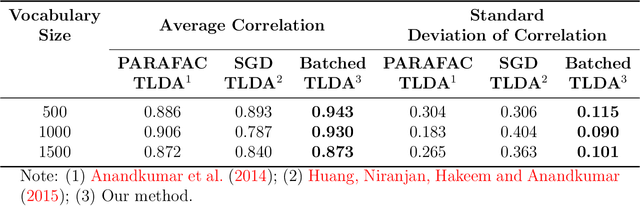
Abstract:This paper proposes a topic modeling method that scales linearly to billions of documents. We make three core contributions: i) we present a topic modeling method, Tensor Latent Dirichlet Allocation (TLDA), that has identifiable and recoverable parameter guarantees and sample complexity guarantees for large data; ii) we show that this method is computationally and memory efficient (achieving speeds over 3-4x those of prior parallelized Latent Dirichlet Allocation (LDA) methods), and that it scales linearly to text datasets with over a billion documents; iii) we provide an open-source, GPU-based implementation, of this method. This scaling enables previously prohibitive analyses, and we perform two real-world, large-scale new studies of interest to political scientists: we provide the first thorough analysis of the evolution of the #MeToo movement through the lens of over two years of Twitter conversation and a detailed study of social media conversations about election fraud in the 2020 presidential election. Thus this method provides social scientists with the ability to study very large corpora at scale and to answer important theoretically-relevant questions about salient issues in near real-time.
FourCastNet 3: A geometric approach to probabilistic machine-learning weather forecasting at scale
Jul 16, 2025Abstract:FourCastNet 3 advances global weather modeling by implementing a scalable, geometric machine learning (ML) approach to probabilistic ensemble forecasting. The approach is designed to respect spherical geometry and to accurately model the spatially correlated probabilistic nature of the problem, resulting in stable spectra and realistic dynamics across multiple scales. FourCastNet 3 delivers forecasting accuracy that surpasses leading conventional ensemble models and rivals the best diffusion-based methods, while producing forecasts 8 to 60 times faster than these approaches. In contrast to other ML approaches, FourCastNet 3 demonstrates excellent probabilistic calibration and retains realistic spectra, even at extended lead times of up to 60 days. All of these advances are realized using a purely convolutional neural network architecture tailored for spherical geometry. Scalable and efficient large-scale training on 1024 GPUs and more is enabled by a novel training paradigm for combined model- and data-parallelism, inspired by domain decomposition methods in classical numerical models. Additionally, FourCastNet 3 enables rapid inference on a single GPU, producing a 90-day global forecast at 0.25{\deg}, 6-hourly resolution in under 20 seconds. Its computational efficiency, medium-range probabilistic skill, spectral fidelity, and rollout stability at subseasonal timescales make it a strong candidate for improving meteorological forecasting and early warning systems through large ensemble predictions.
Principled Approaches for Extending Neural Architectures to Function Spaces for Operator Learning
Jun 12, 2025Abstract:A wide range of scientific problems, such as those described by continuous-time dynamical systems and partial differential equations (PDEs), are naturally formulated on function spaces. While function spaces are typically infinite-dimensional, deep learning has predominantly advanced through applications in computer vision and natural language processing that focus on mappings between finite-dimensional spaces. Such fundamental disparities in the nature of the data have limited neural networks from achieving a comparable level of success in scientific applications as seen in other fields. Neural operators are a principled way to generalize neural networks to mappings between function spaces, offering a pathway to replicate deep learning's transformative impact on scientific problems. For instance, neural operators can learn solution operators for entire classes of PDEs, e.g., physical systems with different boundary conditions, coefficient functions, and geometries. A key factor in deep learning's success has been the careful engineering of neural architectures through extensive empirical testing. Translating these neural architectures into neural operators allows operator learning to enjoy these same empirical optimizations. However, prior neural operator architectures have often been introduced as standalone models, not directly derived as extensions of existing neural network architectures. In this paper, we identify and distill the key principles for constructing practical implementations of mappings between infinite-dimensional function spaces. Using these principles, we propose a recipe for converting several popular neural architectures into neural operators with minimal modifications. This paper aims to guide practitioners through this process and details the steps to make neural operators work in practice. Our code can be found at https://github.com/neuraloperator/NNs-to-NOs
Enabling Automatic Differentiation with Mollified Graph Neural Operators
Apr 11, 2025Abstract:Physics-informed neural operators offer a powerful framework for learning solution operators of partial differential equations (PDEs) by combining data and physics losses. However, these physics losses rely on derivatives. Computing these derivatives remains challenging, with spectral and finite difference methods introducing approximation errors due to finite resolution. Here, we propose the mollified graph neural operator (mGNO), the first method to leverage automatic differentiation and compute \emph{exact} gradients on arbitrary geometries. This enhancement enables efficient training on irregular grids and varying geometries while allowing seamless evaluation of physics losses at randomly sampled points for improved generalization. For a PDE example on regular grids, mGNO paired with autograd reduced the L2 relative data error by 20x compared to finite differences, although training was slower. It can also solve PDEs on unstructured point clouds seamlessly, using physics losses only, at resolutions vastly lower than those needed for finite differences to be accurate enough. On these unstructured point clouds, mGNO leads to errors that are consistently 2 orders of magnitude lower than machine learning baselines (Meta-PDE) for comparable runtimes, and also delivers speedups from 1 to 3 orders of magnitude compared to the numerical solver for similar accuracy. mGNOs can also be used to solve inverse design and shape optimization problems on complex geometries.
Factorized Implicit Global Convolution for Automotive Computational Fluid Dynamics Prediction
Feb 06, 2025Abstract:Computational Fluid Dynamics (CFD) is crucial for automotive design, requiring the analysis of large 3D point clouds to study how vehicle geometry affects pressure fields and drag forces. However, existing deep learning approaches for CFD struggle with the computational complexity of processing high-resolution 3D data. We propose Factorized Implicit Global Convolution (FIGConv), a novel architecture that efficiently solves CFD problems for very large 3D meshes with arbitrary input and output geometries. FIGConv achieves quadratic complexity $O(N^2)$, a significant improvement over existing 3D neural CFD models that require cubic complexity $O(N^3)$. Our approach combines Factorized Implicit Grids to approximate high-resolution domains, efficient global convolutions through 2D reparameterization, and a U-shaped architecture for effective information gathering and integration. We validate our approach on the industry-standard Ahmed body dataset and the large-scale DrivAerNet dataset. In DrivAerNet, our model achieves an $R^2$ value of 0.95 for drag prediction, outperforming the previous state-of-the-art by a significant margin. This represents a 40% improvement in relative mean squared error and a 70% improvement in absolute mean squared error over previous methods.
Tensor-GaLore: Memory-Efficient Training via Gradient Tensor Decomposition
Jan 04, 2025



Abstract:We present Tensor-GaLore, a novel method for efficient training of neural networks with higher-order tensor weights. Many models, particularly those used in scientific computing, employ tensor-parameterized layers to capture complex, multidimensional relationships. When scaling these methods to high-resolution problems makes memory usage grow intractably, and matrix based optimization methods lead to suboptimal performance and compression. We propose to work directly in the high-order space of the complex tensor parameter space using a tensor factorization of the gradients during optimization. We showcase its effectiveness on Fourier Neural Operators (FNOs), a class of models crucial for solving partial differential equations (PDE) and prove the theory of it. Across various PDE tasks like the Navier Stokes and Darcy Flow equations, Tensor-GaLore achieves substantial memory savings, reducing optimizer memory usage by up to 75%. These substantial memory savings across AI for science demonstrate Tensor-GaLore's potential.
A Library for Learning Neural Operators
Dec 13, 2024
Abstract:We present NeuralOperator, an open-source Python library for operator learning. Neural operators generalize neural networks to maps between function spaces instead of finite-dimensional Euclidean spaces. They can be trained and inferenced on input and output functions given at various discretizations, satisfying a discretization convergence properties. Built on top of PyTorch, NeuralOperator provides all the tools for training and deploying neural operator models, as well as developing new ones, in a high-quality, tested, open-source package. It combines cutting-edge models and customizability with a gentle learning curve and simple user interface for newcomers.
Exploring the design space of deep-learning-based weather forecasting systems
Oct 09, 2024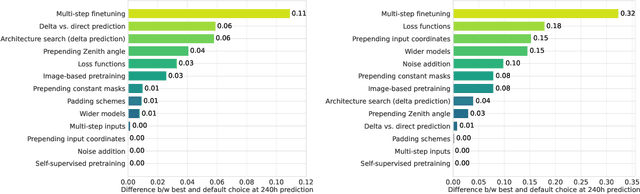

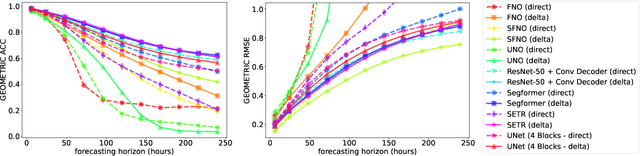
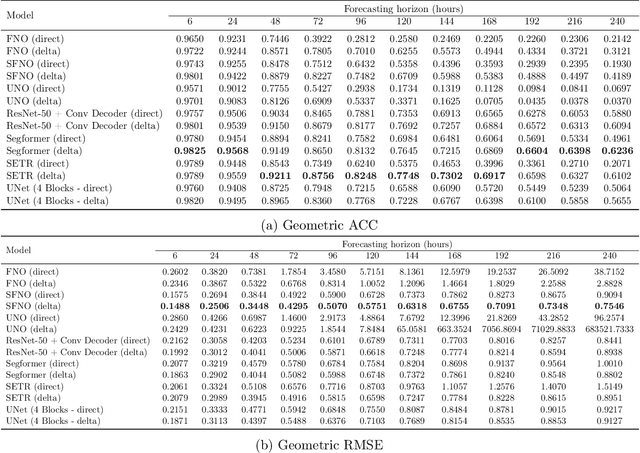
Abstract:Despite tremendous progress in developing deep-learning-based weather forecasting systems, their design space, including the impact of different design choices, is yet to be well understood. This paper aims to fill this knowledge gap by systematically analyzing these choices including architecture, problem formulation, pretraining scheme, use of image-based pretrained models, loss functions, noise injection, multi-step inputs, additional static masks, multi-step finetuning (including larger stride models), as well as training on a larger dataset. We study fixed-grid architectures such as UNet, fully convolutional architectures, and transformer-based models, along with grid-invariant architectures, including graph-based and operator-based models. Our results show that fixed-grid architectures outperform grid-invariant architectures, indicating a need for further architectural developments in grid-invariant models such as neural operators. We therefore propose a hybrid system that combines the strong performance of fixed-grid models with the flexibility of grid-invariant architectures. We further show that multi-step fine-tuning is essential for most deep-learning models to work well in practice, which has been a common practice in the past. Pretraining objectives degrade performance in comparison to supervised training, while image-based pretrained models provide useful inductive biases in some cases in comparison to training the model from scratch. Interestingly, we see a strong positive effect of using a larger dataset when training a smaller model as compared to training on a smaller dataset for longer. Larger models, on the other hand, primarily benefit from just an increase in the computational budget. We believe that these results will aid in the design of better weather forecasting systems in the future.
Fourier Neural Operators for Learning Dynamics in Quantum Spin Systems
Sep 05, 2024



Abstract:Fourier Neural Operators (FNOs) excel on tasks using functional data, such as those originating from partial differential equations. Such characteristics render them an effective approach for simulating the time evolution of quantum wavefunctions, which is a computationally challenging, yet coveted task for understanding quantum systems. In this manuscript, we use FNOs to model the evolution of random quantum spin systems, so chosen due to their representative quantum dynamics and minimal symmetry. We explore two distinct FNO architectures and examine their performance for learning and predicting time evolution using both random and low-energy input states. Additionally, we apply FNOs to a compact set of Hamiltonian observables ($\sim\text{poly}(n)$) instead of the entire $2^n$ quantum wavefunction, which greatly reduces the size of our inputs and outputs and, consequently, the requisite dimensions of the resulting FNOs. Moreover, this Hamiltonian observable-based method demonstrates that FNOs can effectively distill information from high-dimensional spaces into lower-dimensional spaces. The extrapolation of Hamiltonian observables to times later than those used in training is of particular interest, as this stands to fundamentally increase the simulatability of quantum systems past both the coherence times of contemporary quantum architectures and the circuit-depths of tractable tensor networks.
Pretraining Codomain Attention Neural Operators for Solving Multiphysics PDEs
Mar 19, 2024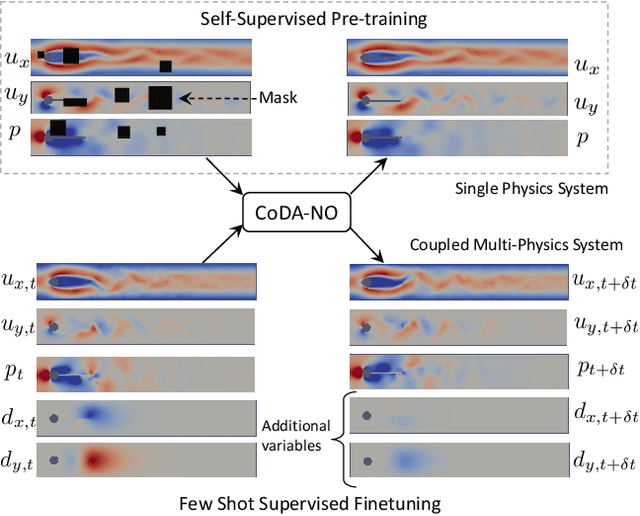

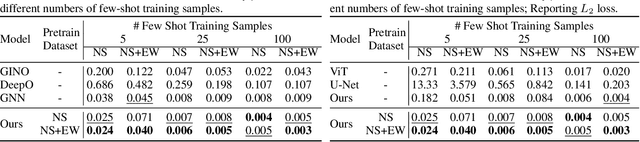
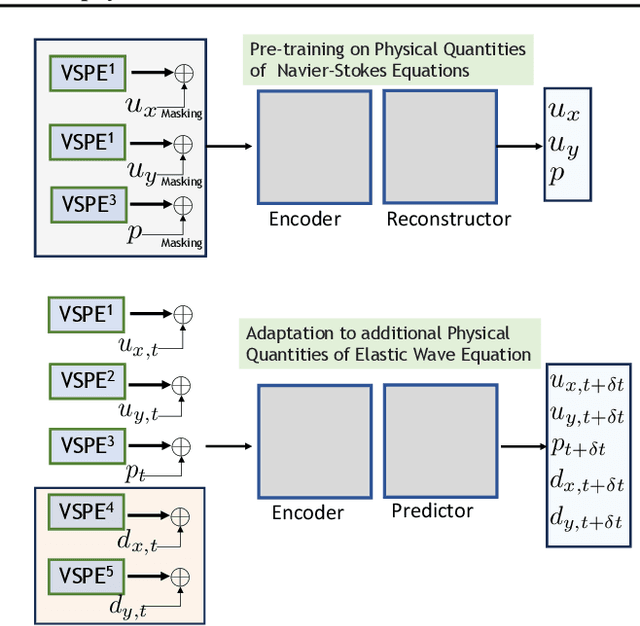
Abstract:Existing neural operator architectures face challenges when solving multiphysics problems with coupled partial differential equations (PDEs), due to complex geometries, interactions between physical variables, and the lack of large amounts of high-resolution training data. To address these issues, we propose Codomain Attention Neural Operator (CoDA-NO), which tokenizes functions along the codomain or channel space, enabling self-supervised learning or pretraining of multiple PDE systems. Specifically, we extend positional encoding, self-attention, and normalization layers to the function space. CoDA-NO can learn representations of different PDE systems with a single model. We evaluate CoDA-NO's potential as a backbone for learning multiphysics PDEs over multiple systems by considering few-shot learning settings. On complex downstream tasks with limited data, such as fluid flow simulations and fluid-structure interactions, we found CoDA-NO to outperform existing methods on the few-shot learning task by over $36\%$. The code is available at https://github.com/ashiq24/CoDA-NO.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge