GeoAda: Efficiently Finetune Geometric Diffusion Models with Equivariant Adapters

Geometric diffusion models have shown remarkable success in molecular dynamics and structure generation. However, efficiently fine-tuning them for downstream tasks with varying geometric controls remains underexplored. In this work, we propose an SE(3)-equivariant adapter framework ( GeoAda) that enables flexible and parameter-efficient fine-tuning for controlled generative tasks without modifying the original model architecture. GeoAda introduces a structured adapter design: control signals are first encoded through coupling operators, then processed by a trainable copy of selected pretrained model layers, and finally projected back via decoupling operators followed by an equivariant zero-initialized convolution. By fine-tuning only these lightweight adapter modules, GeoAda preserves the model's geometric consistency while mitigating overfitting and catastrophic forgetting. We theoretically prove that the proposed adapters maintain SE(3)-equivariance, ensuring that the geometric inductive biases of the pretrained diffusion model remain intact during adaptation. We demonstrate the wide applicability of GeoAda across diverse geometric control types, including frame control, global control, subgraph control, and a broad range of application domains such as particle dynamics, molecular dynamics, human motion prediction, and molecule generation. Empirical results show that GeoAda achieves state-of-the-art fine-tuning performance while preserving original task accuracy, whereas other baselines experience significant performance degradation due to overfitting and catastrophic forgetting.

Fast and Distributed Equivariant Graph Neural Networks by Virtual Node Learning

Equivariant Graph Neural Networks (GNNs) have achieved remarkable success across diverse scientific applications. However, existing approaches face critical efficiency challenges when scaling to large geometric graphs and suffer significant performance degradation when the input graphs are sparsified for computational tractability. To address these limitations, we introduce FastEGNN and DistEGNN, two novel enhancements to equivariant GNNs for large-scale geometric graphs. FastEGNN employs a key innovation: a small ordered set of virtual nodes that effectively approximates the large unordered graph of real nodes. Specifically, we implement distinct message passing and aggregation mechanisms for different virtual nodes to ensure mutual distinctiveness, and minimize Maximum Mean Discrepancy (MMD) between virtual and real coordinates to achieve global distributedness. This design enables FastEGNN to maintain high accuracy while efficiently processing large-scale sparse graphs. For extremely large-scale geometric graphs, we present DistEGNN, a distributed extension where virtual nodes act as global bridges between subgraphs in different devices, maintaining consistency while dramatically reducing memory and computational overhead. We comprehensively evaluate our models across four challenging domains: N-body systems (100 nodes), protein dynamics (800 nodes), Water-3D (8,000 nodes), and our new Fluid113K benchmark (113,000 nodes). Results demonstrate superior efficiency and performance, establishing new capabilities in large-scale equivariant graph learning. Code is available at https://github.com/GLAD-RUC/DistEGNN.

Reinforced Model Merging

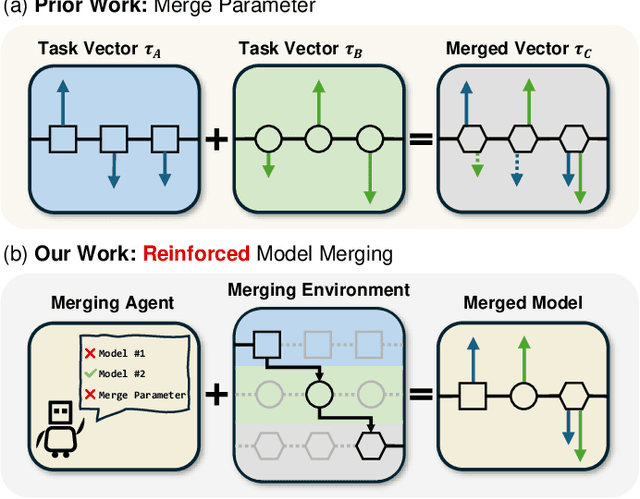
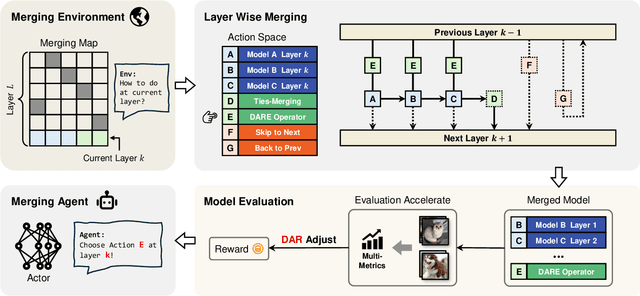
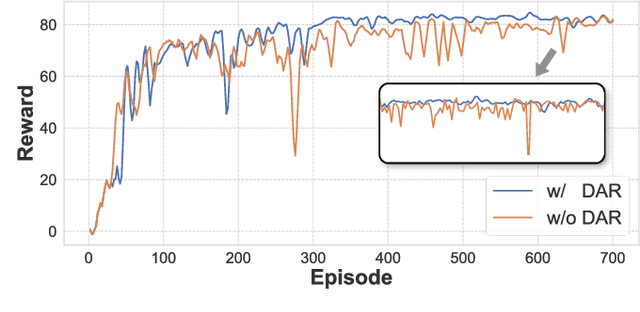
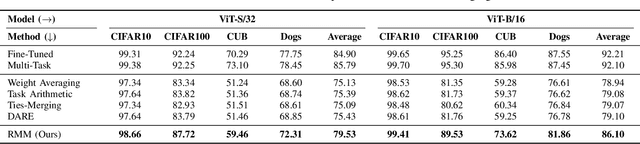
The success of large language models has garnered widespread attention for model merging techniques, especially training-free methods which combine model capabilities within the parameter space. However, two challenges remain: (1) uniform treatment of all parameters leads to performance degradation; (2) search-based algorithms are often inefficient. In this paper, we present an innovative framework termed Reinforced Model Merging (RMM), which encompasses an environment and agent tailored for merging tasks. These components interact to execute layer-wise merging actions, aiming to search the optimal merging architecture. Notably, RMM operates without any gradient computations on the original models, rendering it feasible for edge devices. Furthermore, by utilizing data subsets during the evaluation process, we addressed the bottleneck in the reward feedback phase, thereby accelerating RMM by up to 100 times. Extensive experiments demonstrate that RMM achieves state-of-the-art performance across various vision and NLP datasets and effectively overcomes the limitations of the existing baseline methods. Our code is available at https://github.com/WuDiHJQ/Reinforced-Model-Merging.

Block Diffusion: Interpolating Between Autoregressive and Diffusion Language Models

Diffusion language models offer unique benefits over autoregressive models due to their potential for parallelized generation and controllability, yet they lag in likelihood modeling and are limited to fixed-length generation. In this work, we introduce a class of block diffusion language models that interpolate between discrete denoising diffusion and autoregressive models. Block diffusion overcomes key limitations of both approaches by supporting flexible-length generation and improving inference efficiency with KV caching and parallel token sampling. We propose a recipe for building effective block diffusion models that includes an efficient training algorithm, estimators of gradient variance, and data-driven noise schedules to minimize the variance. Block diffusion sets a new state-of-the-art performance among diffusion models on language modeling benchmarks and enables generation of arbitrary-length sequences. We provide the code, along with the model weights and blog post on the project page: https://m-arriola.com/bd3lms/

$f$-PO: Generalizing Preference Optimization with $f$-divergence Minimization

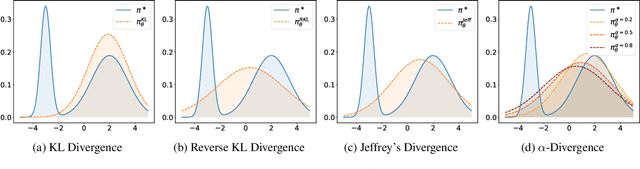
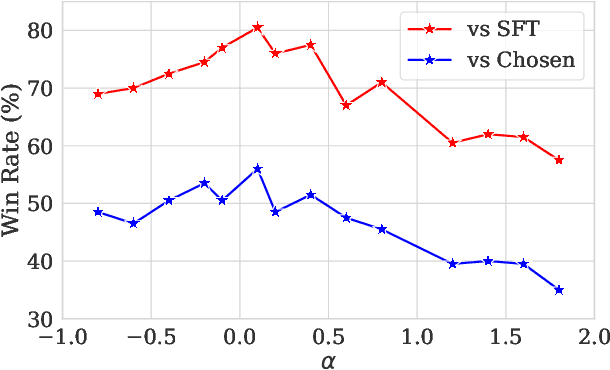
Preference optimization has made significant progress recently, with numerous methods developed to align language models with human preferences. This paper introduces $f$-divergence Preference Optimization ($f$-PO), a novel framework that generalizes and extends existing approaches. $f$-PO minimizes $f$-divergences between the optimized policy and the optimal policy, encompassing a broad family of alignment methods using various divergences. Our approach unifies previous algorithms like DPO and EXO, while offering new variants through different choices of $f$-divergences. We provide theoretical analysis of $f$-PO's properties and conduct extensive experiments on state-of-the-art language models using benchmark datasets. Results demonstrate $f$-PO's effectiveness across various tasks, achieving superior performance compared to existing methods on popular benchmarks such as AlpacaEval 2, Arena-Hard, and MT-Bench. Additionally, we present ablation studies exploring the impact of different $f$-divergences, offering insights into the trade-offs between regularization and performance in offline preference optimization. Our work contributes both practical algorithms and theoretical understanding to the field of language model alignment. Code is available at https://github.com/MinkaiXu/fPO.

Geometric Trajectory Diffusion Models

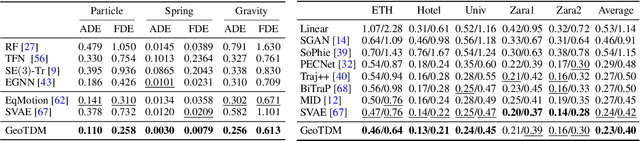
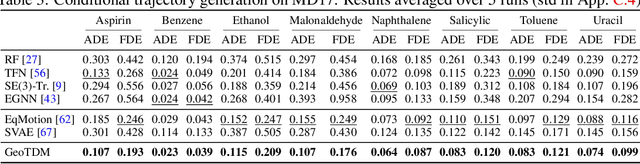
Generative models have shown great promise in generating 3D geometric systems, which is a fundamental problem in many natural science domains such as molecule and protein design. However, existing approaches only operate on static structures, neglecting the fact that physical systems are always dynamic in nature. In this work, we propose geometric trajectory diffusion models (GeoTDM), the first diffusion model for modeling the temporal distribution of 3D geometric trajectories. Modeling such distribution is challenging as it requires capturing both the complex spatial interactions with physical symmetries and temporal correspondence encapsulated in the dynamics. We theoretically justify that diffusion models with equivariant temporal kernels can lead to density with desired symmetry, and develop a novel transition kernel leveraging SE(3)-equivariant spatial convolution and temporal attention. Furthermore, to induce an expressive trajectory distribution for conditional generation, we introduce a generalized learnable geometric prior into the forward diffusion process to enhance temporal conditioning. We conduct extensive experiments on both unconditional and conditional generation in various scenarios, including physical simulation, molecular dynamics, and pedestrian motion. Empirical results on a wide suite of metrics demonstrate that GeoTDM can generate realistic geometric trajectories with significantly higher quality.

TFG: Unified Training-Free Guidance for Diffusion Models

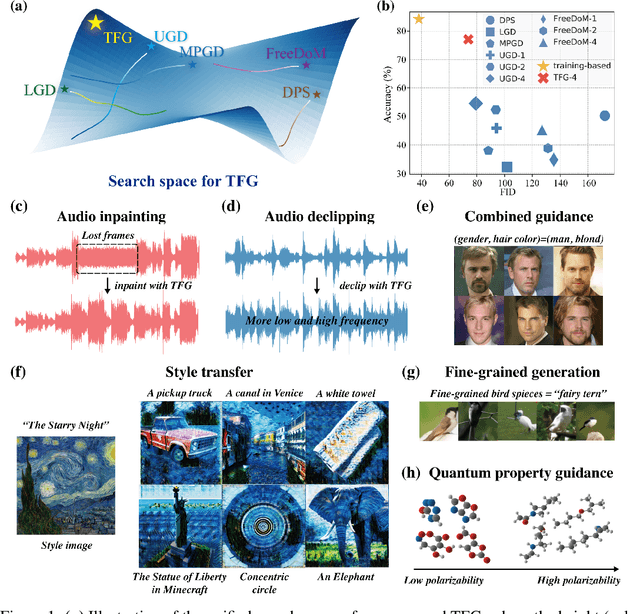
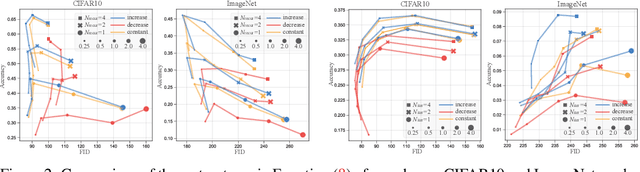
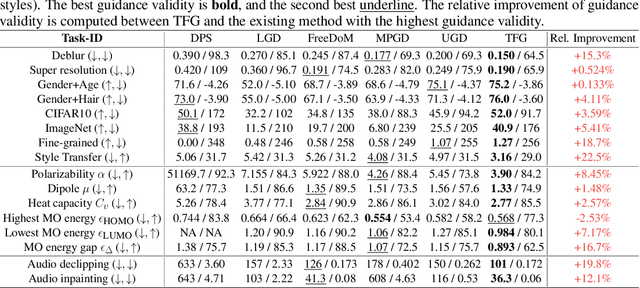
Given an unconditional diffusion model and a predictor for a target property of interest (e.g., a classifier), the goal of training-free guidance is to generate samples with desirable target properties without additional training. Existing methods, though effective in various individual applications, often lack theoretical grounding and rigorous testing on extensive benchmarks. As a result, they could even fail on simple tasks, and applying them to a new problem becomes unavoidably difficult. This paper introduces a novel algorithmic framework encompassing existing methods as special cases, unifying the study of training-free guidance into the analysis of an algorithm-agnostic design space. Via theoretical and empirical investigation, we propose an efficient and effective hyper-parameter searching strategy that can be readily applied to any downstream task. We systematically benchmark across 7 diffusion models on 16 tasks with 40 targets, and improve performance by 8.5% on average. Our framework and benchmark offer a solid foundation for conditional generation in a training-free manner.

CPSample: Classifier Protected Sampling for Guarding Training Data During Diffusion

Diffusion models have a tendency to exactly replicate their training data, especially when trained on small datasets. Most prior work has sought to mitigate this problem by imposing differential privacy constraints or masking parts of the training data, resulting in a notable substantial decrease in image quality. We present CPSample, a method that modifies the sampling process to prevent training data replication while preserving image quality. CPSample utilizes a classifier that is trained to overfit on random binary labels attached to the training data. CPSample then uses classifier guidance to steer the generation process away from the set of points that can be classified with high certainty, a set that includes the training data. CPSample achieves FID scores of 4.97 and 2.97 on CIFAR-10 and CelebA-64, respectively, without producing exact replicates of the training data. Unlike prior methods intended to guard the training images, CPSample only requires training a classifier rather than retraining a diffusion model, which is computationally cheaper. Moreover, our technique provides diffusion models with greater robustness against membership inference attacks, wherein an adversary attempts to discern which images were in the model's training dataset. We show that CPSample behaves like a built-in rejection sampler, and we demonstrate its capabilities to prevent mode collapse in Stable Diffusion.

RelBench: A Benchmark for Deep Learning on Relational Databases

We present RelBench, a public benchmark for solving predictive tasks over relational databases with graph neural networks. RelBench provides databases and tasks spanning diverse domains and scales, and is intended to be a foundational infrastructure for future research. We use RelBench to conduct the first comprehensive study of Relational Deep Learning (RDL) (Fey et al., 2024), which combines graph neural network predictive models with (deep) tabular models that extract initial entity-level representations from raw tables. End-to-end learned RDL models fully exploit the predictive signal encoded in primary-foreign key links, marking a significant shift away from the dominant paradigm of manual feature engineering combined with tabular models. To thoroughly evaluate RDL against this prior gold-standard, we conduct an in-depth user study where an experienced data scientist manually engineers features for each task. In this study, RDL learns better models whilst reducing human work needed by more than an order of magnitude. This demonstrates the power of deep learning for solving predictive tasks over relational databases, opening up many new research opportunities enabled by RelBench.

Img2CAD: Reverse Engineering 3D CAD Models from Images through VLM-Assisted Conditional Factorization

Reverse engineering 3D computer-aided design (CAD) models from images is an important task for many downstream applications including interactive editing, manufacturing, architecture, robotics, etc. The difficulty of the task lies in vast representational disparities between the CAD output and the image input. CAD models are precise, programmatic constructs that involves sequential operations combining discrete command structure with continuous attributes -- making it challenging to learn and optimize in an end-to-end fashion. Concurrently, input images introduce inherent challenges such as photo-metric variability and sensor noise, complicating the reverse engineering process. In this work, we introduce a novel approach that conditionally factorizes the task into two sub-problems. First, we leverage large foundation models, particularly GPT-4V, to predict the global discrete base structure with semantic information. Second, we propose TrAssembler that conditioned on the discrete structure with semantics predicts the continuous attribute values. To support the training of our TrAssembler, we further constructed an annotated CAD dataset of common objects from ShapeNet. Putting all together, our approach and data demonstrate significant first steps towards CAD-ifying images in the wild. Our project page: https://anonymous123342.github.io/