The Diffusion Duality

Uniform-state discrete diffusion models hold the promise of fast text generation due to their inherent ability to self-correct. However, they are typically outperformed by autoregressive models and masked diffusion models. In this work, we narrow this performance gap by leveraging a key insight: Uniform-state diffusion processes naturally emerge from an underlying Gaussian diffusion. Our method, Duo, transfers powerful techniques from Gaussian diffusion to improve both training and sampling. First, we introduce a curriculum learning strategy guided by the Gaussian process, doubling training speed by reducing variance. Models trained with curriculum learning surpass autoregressive models in zero-shot perplexity on 3 of 7 benchmarks. Second, we present Discrete Consistency Distillation, which adapts consistency distillation from the continuous to the discrete setting. This algorithm unlocks few-step generation in diffusion language models by accelerating sampling by two orders of magnitude. We provide the code and model checkpoints on the project page: http://s-sahoo.github.io/duo

RanDeS: Randomized Delta Superposition for Multi-Model Compression

From a multi-model compression perspective, model merging enables memory-efficient serving of multiple models fine-tuned from the same base, but suffers from degraded performance due to interference among their task-specific parameter adjustments (i.e., deltas). In this paper, we reformulate model merging as a compress-and-retrieve scheme, revealing that the task interference arises from the summation of irrelevant deltas during model retrieval. To address this issue, we use random orthogonal transformations to decorrelate these vectors into self-cancellation. We show that this approach drastically reduces interference, improving performance across both vision and language tasks. Since these transformations are fully defined by random seeds, adding new models requires no extra memory. Further, their data- and model-agnostic nature enables easy addition or removal of models with minimal compute overhead, supporting efficient and flexible multi-model serving.

Block Diffusion: Interpolating Between Autoregressive and Diffusion Language Models

Diffusion language models offer unique benefits over autoregressive models due to their potential for parallelized generation and controllability, yet they lag in likelihood modeling and are limited to fixed-length generation. In this work, we introduce a class of block diffusion language models that interpolate between discrete denoising diffusion and autoregressive models. Block diffusion overcomes key limitations of both approaches by supporting flexible-length generation and improving inference efficiency with KV caching and parallel token sampling. We propose a recipe for building effective block diffusion models that includes an efficient training algorithm, estimators of gradient variance, and data-driven noise schedules to minimize the variance. Block diffusion sets a new state-of-the-art performance among diffusion models on language modeling benchmarks and enables generation of arbitrary-length sequences. We provide the code, along with the model weights and blog post on the project page: https://m-arriola.com/bd3lms/

The GAN is dead; long live the GAN! A Modern GAN Baseline

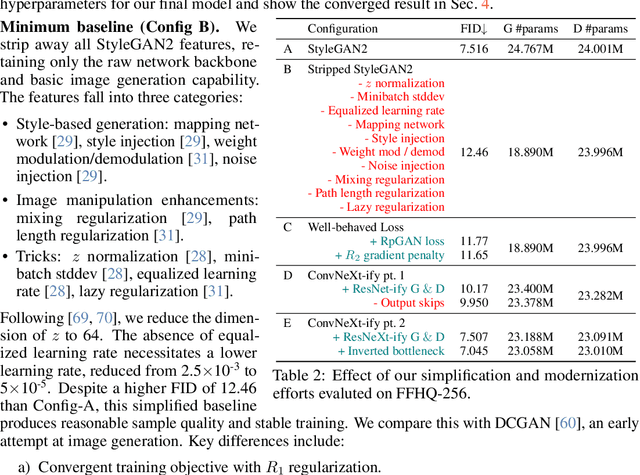
There is a widely-spread claim that GANs are difficult to train, and GAN architectures in the literature are littered with empirical tricks. We provide evidence against this claim and build a modern GAN baseline in a more principled manner. First, we derive a well-behaved regularized relativistic GAN loss that addresses issues of mode dropping and non-convergence that were previously tackled via a bag of ad-hoc tricks. We analyze our loss mathematically and prove that it admits local convergence guarantees, unlike most existing relativistic losses. Second, our new loss allows us to discard all ad-hoc tricks and replace outdated backbones used in common GANs with modern architectures. Using StyleGAN2 as an example, we present a roadmap of simplification and modernization that results in a new minimalist baseline -- R3GAN. Despite being simple, our approach surpasses StyleGAN2 on FFHQ, ImageNet, CIFAR, and Stacked MNIST datasets, and compares favorably against state-of-the-art GANs and diffusion models.

Simple Guidance Mechanisms for Discrete Diffusion Models

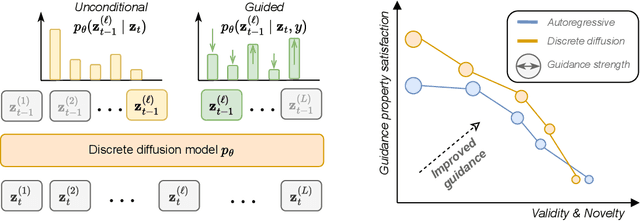
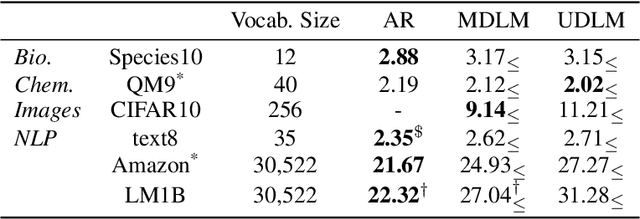
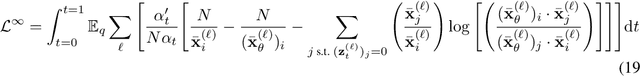
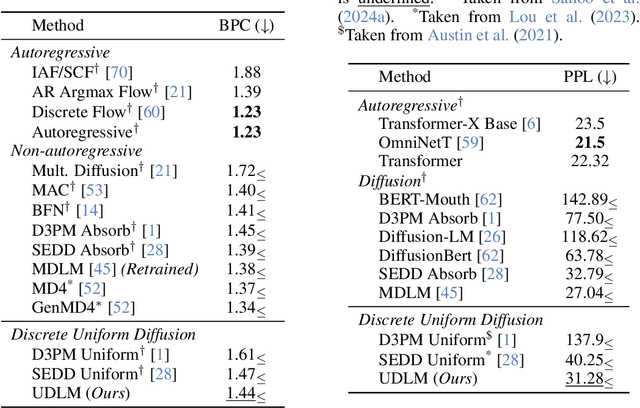
Diffusion models for continuous data gained widespread adoption owing to their high quality generation and control mechanisms. However, controllable diffusion on discrete data faces challenges given that continuous guidance methods do not directly apply to discrete diffusion. Here, we provide a straightforward derivation of classifier-free and classifier-based guidance for discrete diffusion, as well as a new class of diffusion models that leverage uniform noise and that are more guidable because they can continuously edit their outputs. We improve the quality of these models with a novel continuous-time variational lower bound that yields state-of-the-art performance, especially in settings involving guidance or fast generation. Empirically, we demonstrate that our guidance mechanisms combined with uniform noise diffusion improve controllable generation relative to autoregressive and diffusion baselines on several discrete data domains, including genomic sequences, small molecule design, and discretized image generation.

Calibrated Probabilistic Forecasts for Arbitrary Sequences

Real-world data streams can change unpredictably due to distribution shifts, feedback loops and adversarial actors, which challenges the validity of forecasts. We present a forecasting framework ensuring valid uncertainty estimates regardless of how data evolves. Leveraging the concept of Blackwell approachability from game theory, we introduce a forecasting framework that guarantees calibrated uncertainties for outcomes in any compact space (e.g., classification or bounded regression). We extend this framework to recalibrate existing forecasters, guaranteeing accurate uncertainties without sacrificing predictive performance. We implement both general-purpose gradient-based algorithms and algorithms optimized for popular special cases of our framework. Empirically, our algorithms improve calibration and downstream decision-making for energy systems.

Simple and Effective Masked Diffusion Language Models

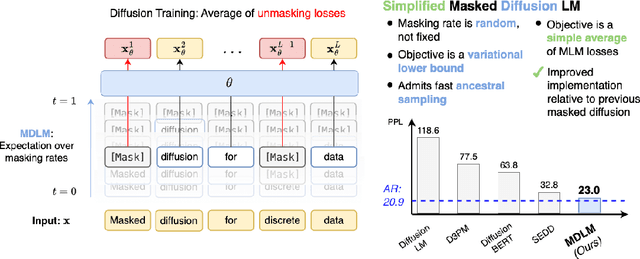
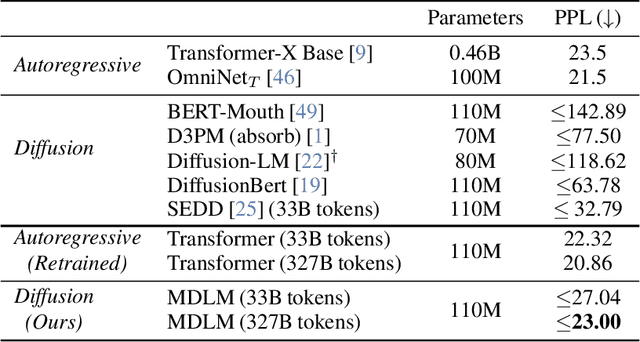
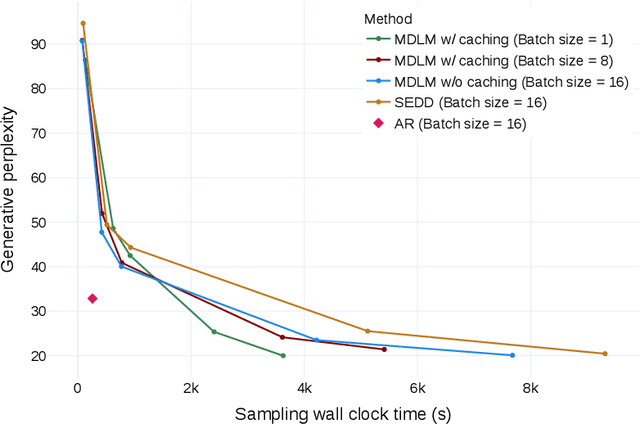
While diffusion models excel at generating high-quality images, prior work reports a significant performance gap between diffusion and autoregressive (AR) methods in language modeling. In this work, we show that simple masked discrete diffusion is more performant than previously thought. We apply an effective training recipe that improves the performance of masked diffusion models and derive a simplified, Rao-Blackwellized objective that results in additional improvements. Our objective has a simple form -- it is a mixture of classical masked language modeling losses -- and can be used to train encoder-only language models that admit efficient samplers, including ones that can generate arbitrary lengths of text semi-autoregressively like a traditional language model. On language modeling benchmarks, a range of masked diffusion models trained with modern engineering practices achieves a new state-of-the-art among diffusion models, and approaches AR perplexity. We release our code at: https://github.com/kuleshov-group/mdlm

Caduceus: Bi-Directional Equivariant Long-Range DNA Sequence Modeling

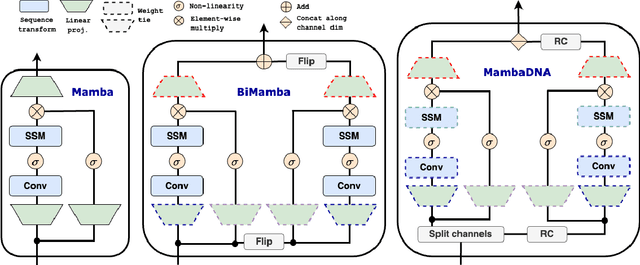
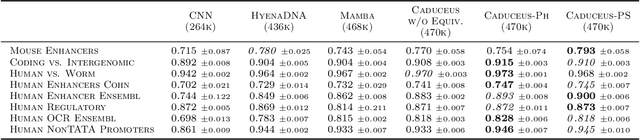
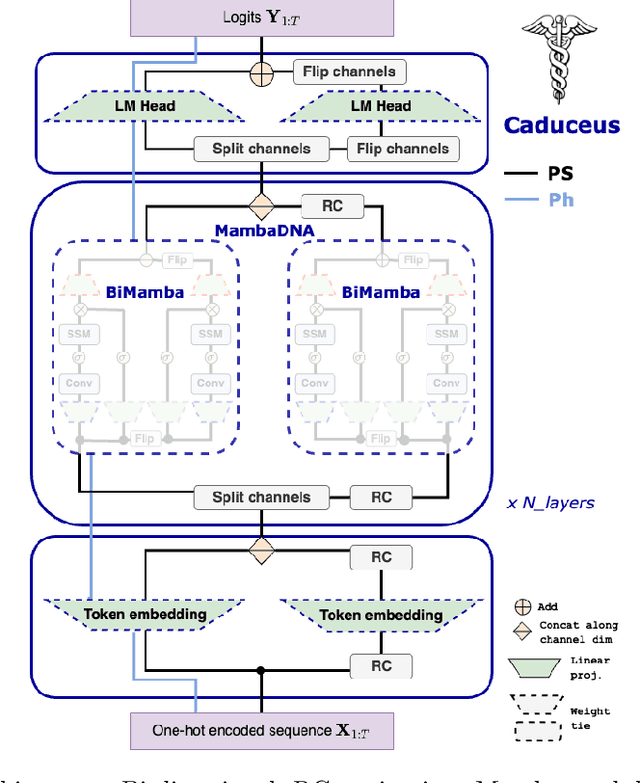
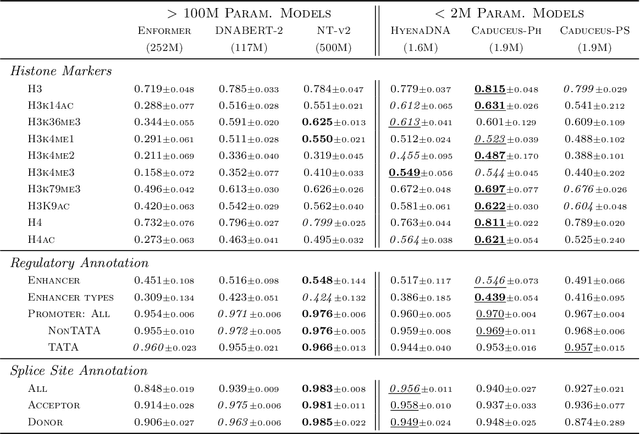
Large-scale sequence modeling has sparked rapid advances that now extend into biology and genomics. However, modeling genomic sequences introduces challenges such as the need to model long-range token interactions, the effects of upstream and downstream regions of the genome, and the reverse complementarity (RC) of DNA. Here, we propose an architecture motivated by these challenges that builds off the long-range Mamba block, and extends it to a BiMamba component that supports bi-directionality, and to a MambaDNA block that additionally supports RC equivariance. We use MambaDNA as the basis of Caduceus, the first family of RC equivariant bi-directional long-range DNA language models, and we introduce pre-training and fine-tuning strategies that yield Caduceus DNA foundation models. Caduceus outperforms previous long-range models on downstream benchmarks; on a challenging long-range variant effect prediction task, Caduceus exceeds the performance of 10x larger models that do not leverage bi-directionality or equivariance.

QuIP#: Even Better LLM Quantization with Hadamard Incoherence and Lattice Codebooks

Post-training quantization (PTQ) reduces the memory footprint of LLMs by quantizing their weights to low-precision. In this work, we introduce QuIP#, a weight-only PTQ method that achieves state-of-the-art results in extreme compression regimes ($\le$ 4 bits per weight) using three novel techniques. First, QuIP# improves the incoherence processing from QuIP by using the randomized Hadamard transform, which is faster and has better theoretical properties. Second, QuIP# uses vector quantization techniques to take advantage of the ball-shaped sub-Gaussian distribution that incoherent weights possess: specifically, we introduce a set of hardware-efficient codebooks based on the highly symmetric $E_8$ lattice, which achieves the optimal 8-dimension unit ball packing. Third, QuIP# uses fine-tuning to improve fidelity to the original model. Our experiments show that QuIP# outperforms existing PTQ methods, enables new behaviors in PTQ scaling, and supports fast inference.

DySLIM: Dynamics Stable Learning by Invariant Measure for Chaotic Systems

Learning dynamics from dissipative chaotic systems is notoriously difficult due to their inherent instability, as formalized by their positive Lyapunov exponents, which exponentially amplify errors in the learned dynamics. However, many of these systems exhibit ergodicity and an attractor: a compact and highly complex manifold, to which trajectories converge in finite-time, that supports an invariant measure, i.e., a probability distribution that is invariant under the action of the dynamics, which dictates the long-term statistical behavior of the system. In this work, we leverage this structure to propose a new framework that targets learning the invariant measure as well as the dynamics, in contrast with typical methods that only target the misfit between trajectories, which often leads to divergence as the trajectories' length increases. We use our framework to propose a tractable and sample efficient objective that can be used with any existing learning objectives. Our Dynamics Stable Learning by Invariant Measures (DySLIM) objective enables model training that achieves better point-wise tracking and long-term statistical accuracy relative to other learning objectives. By targeting the distribution with a scalable regularization term, we hope that this approach can be extended to more complex systems exhibiting slowly-variant distributions, such as weather and climate models.