Neural general circulation models optimized to predict satellite-based precipitation observations

Climate models struggle to accurately simulate precipitation, particularly extremes and the diurnal cycle. Here, we present a hybrid model that is trained directly on satellite-based precipitation observations. Our model runs at 2.8$^\circ$ resolution and is built on the differentiable NeuralGCM framework. The model demonstrates significant improvements over existing general circulation models, the ERA5 reanalysis, and a global cloud-resolving model in simulating precipitation. Our approach yields reduced biases, a more realistic precipitation distribution, improved representation of extremes, and a more accurate diurnal cycle. Furthermore, it outperforms the mid-range precipitation forecast of the ECMWF ensemble. This advance paves the way for more reliable simulations of current climate and demonstrates how training on observations can be used to directly improve GCMs.

4D-Var using Hessian approximation and backpropagation applied to automatically-differentiable numerical and machine learning models

Constraining a numerical weather prediction (NWP) model with observations via 4D variational (4D-Var) data assimilation is often difficult to implement in practice due to the need to develop and maintain a software-based tangent linear model and adjoint model. One of the most common 4D-Var algorithms uses an incremental update procedure, which has been shown to be an approximation of the Gauss-Newton method. Here we demonstrate that when using a forecast model that supports automatic differentiation, an efficient and in some cases more accurate alternative approximation of the Gauss-Newton method can be applied by combining backpropagation of errors with Hessian approximation. This approach can be used with either a conventional numerical model implemented within a software framework that supports automatic differentiation, or a machine learning (ML) based surrogate model. We test the new approach on a variety of Lorenz-96 and quasi-geostrophic models. The results indicate potential for a deeper integration of modeling, data assimilation, and new technologies in a next-generation of operational forecast systems that leverage weather models designed to support automatic differentiation.

DySLIM: Dynamics Stable Learning by Invariant Measure for Chaotic Systems

Learning dynamics from dissipative chaotic systems is notoriously difficult due to their inherent instability, as formalized by their positive Lyapunov exponents, which exponentially amplify errors in the learned dynamics. However, many of these systems exhibit ergodicity and an attractor: a compact and highly complex manifold, to which trajectories converge in finite-time, that supports an invariant measure, i.e., a probability distribution that is invariant under the action of the dynamics, which dictates the long-term statistical behavior of the system. In this work, we leverage this structure to propose a new framework that targets learning the invariant measure as well as the dynamics, in contrast with typical methods that only target the misfit between trajectories, which often leads to divergence as the trajectories' length increases. We use our framework to propose a tractable and sample efficient objective that can be used with any existing learning objectives. Our Dynamics Stable Learning by Invariant Measures (DySLIM) objective enables model training that achieves better point-wise tracking and long-term statistical accuracy relative to other learning objectives. By targeting the distribution with a scalable regularization term, we hope that this approach can be extended to more complex systems exhibiting slowly-variant distributions, such as weather and climate models.

Neural General Circulation Models

General circulation models (GCMs) are the foundation of weather and climate prediction. GCMs are physics-based simulators which combine a numerical solver for large-scale dynamics with tuned representations for small-scale processes such as cloud formation. Recently, machine learning (ML) models trained on reanalysis data achieved comparable or better skill than GCMs for deterministic weather forecasting. However, these models have not demonstrated improved ensemble forecasts, or shown sufficient stability for long-term weather and climate simulations. Here we present the first GCM that combines a differentiable solver for atmospheric dynamics with ML components, and show that it can generate forecasts of deterministic weather, ensemble weather and climate on par with the best ML and physics-based methods. NeuralGCM is competitive with ML models for 1-10 day forecasts, and with the European Centre for Medium-Range Weather Forecasts ensemble prediction for 1-15 day forecasts. With prescribed sea surface temperature, NeuralGCM can accurately track climate metrics such as global mean temperature for multiple decades, and climate forecasts with 140 km resolution exhibit emergent phenomena such as realistic frequency and trajectories of tropical cyclones. For both weather and climate, our approach offers orders of magnitude computational savings over conventional GCMs. Our results show that end-to-end deep learning is compatible with tasks performed by conventional GCMs, and can enhance the large-scale physical simulations that are essential for understanding and predicting the Earth system.

WeatherBench 2: A benchmark for the next generation of data-driven global weather models

WeatherBench 2 is an update to the global, medium-range (1-14 day) weather forecasting benchmark proposed by Rasp et al. (2020), designed with the aim to accelerate progress in data-driven weather modeling. WeatherBench 2 consists of an open-source evaluation framework, publicly available training, ground truth and baseline data as well as a continuously updated website with the latest metrics and state-of-the-art models: https://sites.research.google/weatherbench. This paper describes the design principles of the evaluation framework and presents results for current state-of-the-art physical and data-driven weather models. The metrics are based on established practices for evaluating weather forecasts at leading operational weather centers. We define a set of headline scores to provide an overview of model performance. In addition, we also discuss caveats in the current evaluation setup and challenges for the future of data-driven weather forecasting.

GraphCast: Learning skillful medium-range global weather forecasting

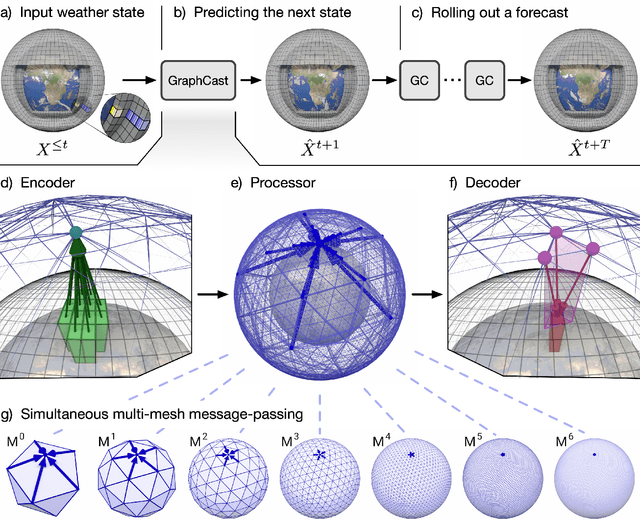
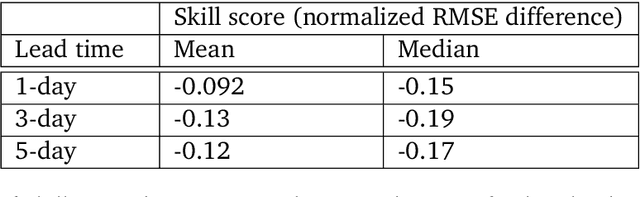
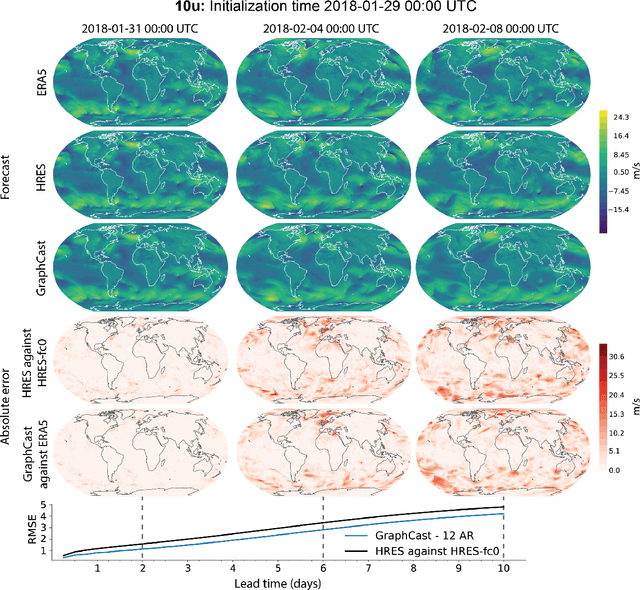
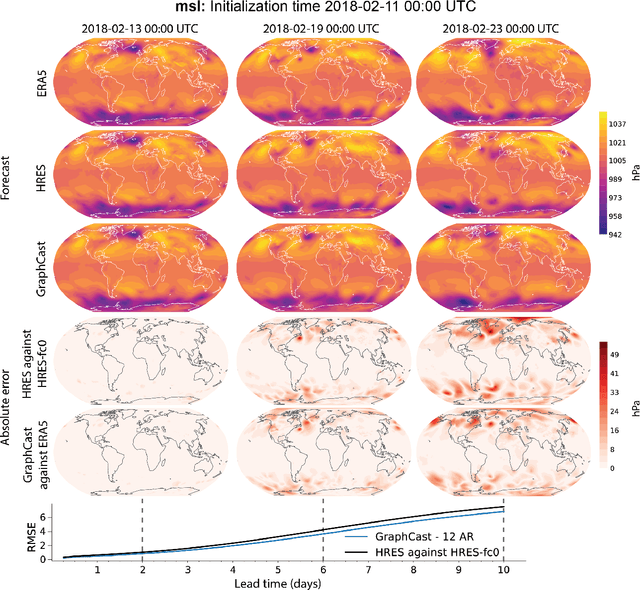
We introduce a machine-learning (ML)-based weather simulator--called "GraphCast"--which outperforms the most accurate deterministic operational medium-range weather forecasting system in the world, as well as all previous ML baselines. GraphCast is an autoregressive model, based on graph neural networks and a novel high-resolution multi-scale mesh representation, which we trained on historical weather data from the European Centre for Medium-Range Weather Forecasts (ECMWF)'s ERA5 reanalysis archive. It can make 10-day forecasts, at 6-hour time intervals, of five surface variables and six atmospheric variables, each at 37 vertical pressure levels, on a 0.25-degree latitude-longitude grid, which corresponds to roughly 25 x 25 kilometer resolution at the equator. Our results show GraphCast is more accurate than ECMWF's deterministic operational forecasting system, HRES, on 90.0% of the 2760 variable and lead time combinations we evaluated. GraphCast also outperforms the most accurate previous ML-based weather forecasting model on 99.2% of the 252 targets it reported. GraphCast can generate a 10-day forecast (35 gigabytes of data) in under 60 seconds on Cloud TPU v4 hardware. Unlike traditional forecasting methods, ML-based forecasting scales well with data: by training on bigger, higher quality, and more recent data, the skill of the forecasts can improve. Together these results represent a key step forward in complementing and improving weather modeling with ML, open new opportunities for fast, accurate forecasting, and help realize the promise of ML-based simulation in the physical sciences.

Learning to correct spectral methods for simulating turbulent flows

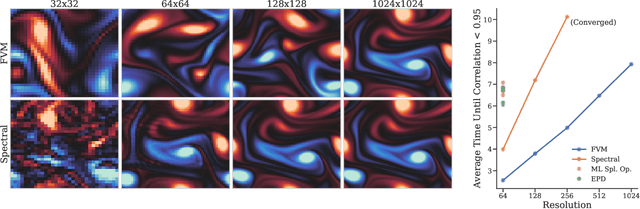
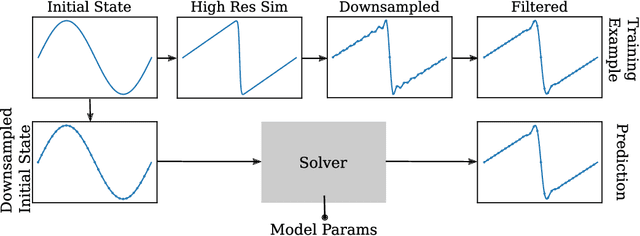
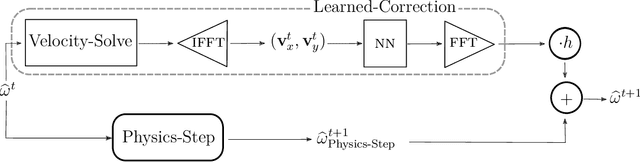
Despite their ubiquity throughout science and engineering, only a handful of partial differential equations (PDEs) have analytical, or closed-form solutions. This motivates a vast amount of classical work on numerical simulation of PDEs and more recently, a whirlwind of research into data-driven techniques leveraging machine learning (ML). A recent line of work indicates that a hybrid of classical numerical techniques with machine learning can offer significant improvements over either approach alone. In this work, we show that the choice of the numerical scheme is crucial when incorporating physics-based priors. We build upon Fourier-based spectral methods, which are considerably more efficient than other numerical schemes for simulating PDEs with smooth and periodic solutions. Specifically, we develop ML-augmented spectral solvers for three model PDEs of fluid dynamics, which improve upon the accuracy of standard spectral solvers at the same resolution. We also demonstrate a handful of key design principles for combining machine learning and numerical methods for solving PDEs.

Efficient and Modular Implicit Differentiation

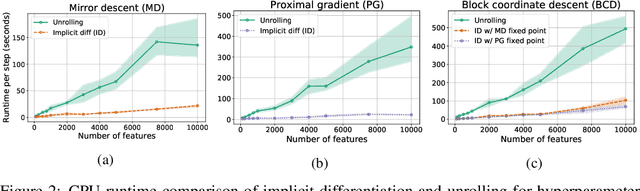
Automatic differentiation (autodiff) has revolutionized machine learning. It allows expressing complex computations by composing elementary ones in creative ways and removes the burden of computing their derivatives by hand. More recently, differentiation of optimization problem solutions has attracted widespread attention with applications such as optimization as a layer, and in bi-level problems such as hyper-parameter optimization and meta-learning. However, the formulas for these derivatives often involve case-by-case tedious mathematical derivations. In this paper, we propose a unified, efficient and modular approach for implicit differentiation of optimization problems. In our approach, the user defines (in Python in the case of our implementation) a function $F$ capturing the optimality conditions of the problem to be differentiated. Once this is done, we leverage autodiff of $F$ and implicit differentiation to automatically differentiate the optimization problem. Our approach thus combines the benefits of implicit differentiation and autodiff. It is efficient as it can be added on top of any state-of-the-art solver and modular as the optimality condition specification is decoupled from the implicit differentiation mechanism. We show that seemingly simple principles allow to recover many recently proposed implicit differentiation methods and create new ones easily. We demonstrate the ease of formulating and solving bi-level optimization problems using our framework. We also showcase an application to the sensitivity analysis of molecular dynamics.

Variational Data Assimilation with a Learned Inverse Observation Operator

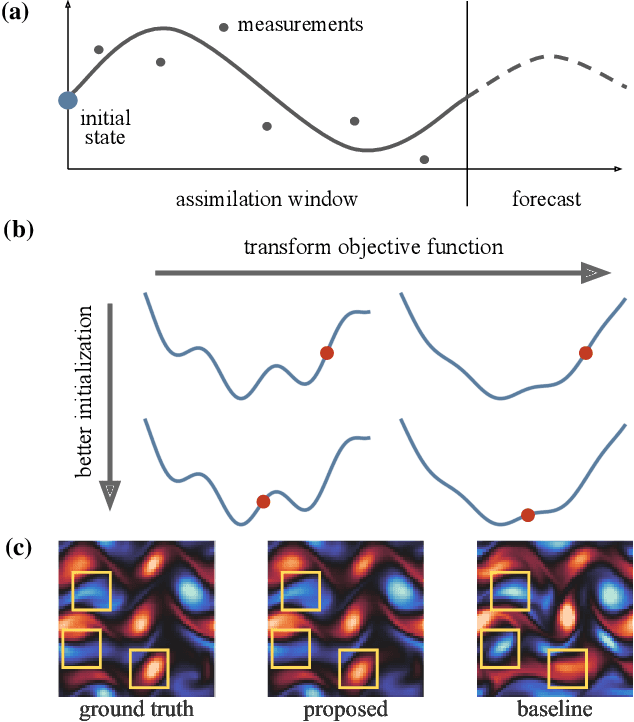
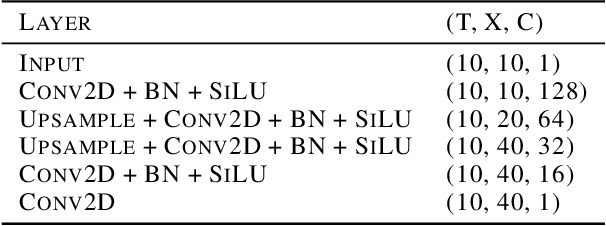
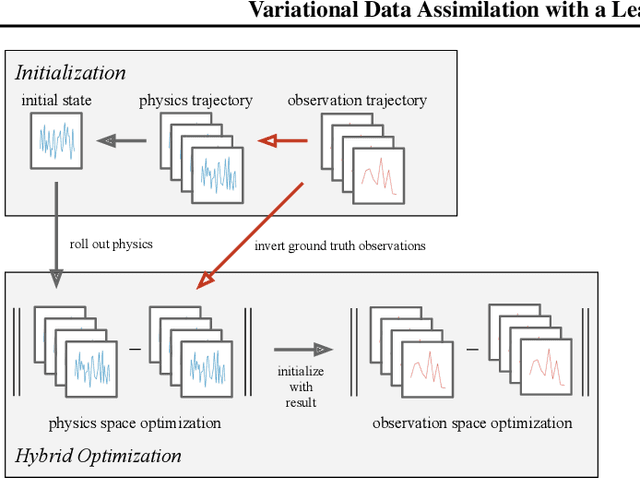
Variational data assimilation optimizes for an initial state of a dynamical system such that its evolution fits observational data. The physical model can subsequently be evolved into the future to make predictions. This principle is a cornerstone of large scale forecasting applications such as numerical weather prediction. As such, it is implemented in current operational systems of weather forecasting agencies across the globe. However, finding a good initial state poses a difficult optimization problem in part due to the non-invertible relationship between physical states and their corresponding observations. We learn a mapping from observational data to physical states and show how it can be used to improve optimizability. We employ this mapping in two ways: to better initialize the non-convex optimization problem, and to reformulate the objective function in better behaved physics space instead of observation space. Our experimental results for the Lorenz96 model and a two-dimensional turbulent fluid flow demonstrate that this procedure significantly improves forecast quality for chaotic systems.

Machine learning accelerated computational fluid dynamics

Numerical simulation of fluids plays an essential role in modeling many physical phenomena, such as weather, climate, aerodynamics and plasma physics. Fluids are well described by the Navier-Stokes equations, but solving these equations at scale remains daunting, limited by the computational cost of resolving the smallest spatiotemporal features. This leads to unfavorable trade-offs between accuracy and tractability. Here we use end-to-end deep learning to improve approximations inside computational fluid dynamics for modeling two-dimensional turbulent flows. For both direct numerical simulation of turbulence and large eddy simulation, our results are as accurate as baseline solvers with 8-10x finer resolution in each spatial dimension, resulting in 40-80x fold computational speedups. Our method remains stable during long simulations, and generalizes to forcing functions and Reynolds numbers outside of the flows where it is trained, in contrast to black box machine learning approaches. Our approach exemplifies how scientific computing can leverage machine learning and hardware accelerators to improve simulations without sacrificing accuracy or generalization.