Neural General Circulation Models

General circulation models (GCMs) are the foundation of weather and climate prediction. GCMs are physics-based simulators which combine a numerical solver for large-scale dynamics with tuned representations for small-scale processes such as cloud formation. Recently, machine learning (ML) models trained on reanalysis data achieved comparable or better skill than GCMs for deterministic weather forecasting. However, these models have not demonstrated improved ensemble forecasts, or shown sufficient stability for long-term weather and climate simulations. Here we present the first GCM that combines a differentiable solver for atmospheric dynamics with ML components, and show that it can generate forecasts of deterministic weather, ensemble weather and climate on par with the best ML and physics-based methods. NeuralGCM is competitive with ML models for 1-10 day forecasts, and with the European Centre for Medium-Range Weather Forecasts ensemble prediction for 1-15 day forecasts. With prescribed sea surface temperature, NeuralGCM can accurately track climate metrics such as global mean temperature for multiple decades, and climate forecasts with 140 km resolution exhibit emergent phenomena such as realistic frequency and trajectories of tropical cyclones. For both weather and climate, our approach offers orders of magnitude computational savings over conventional GCMs. Our results show that end-to-end deep learning is compatible with tasks performed by conventional GCMs, and can enhance the large-scale physical simulations that are essential for understanding and predicting the Earth system.

Score-Based Diffusion Models as Principled Priors for Inverse Imaging

It is important in computational imaging to understand the uncertainty of images reconstructed from imperfect measurements. We propose turning score-based diffusion models into principled priors (``score-based priors'') for analyzing a posterior of images given measurements. Previously, probabilistic priors were limited to handcrafted regularizers and simple distributions. In this work, we empirically validate the theoretically-proven probability function of a score-based diffusion model. We show how to sample from resulting posteriors by using this probability function for variational inference. Our results, including experiments on denoising, deblurring, and interferometric imaging, suggest that score-based priors enable principled inference with a sophisticated, data-driven image prior.

Ensembling over Classifiers: a Bias-Variance Perspective

Ensembles are a straightforward, remarkably effective method for improving the accuracy,calibration, and robustness of models on classification tasks; yet, the reasons that underlie their success remain an active area of research. We build upon the extension to the bias-variance decomposition by Pfau (2013) in order to gain crucial insights into the behavior of ensembles of classifiers. Introducing a dual reparameterization of the bias-variance tradeoff, we first derive generalized laws of total expectation and variance for nonsymmetric losses typical of classification tasks. Comparing conditional and bootstrap bias/variance estimates, we then show that conditional estimates necessarily incur an irreducible error. Next, we show that ensembling in dual space reduces the variance and leaves the bias unchanged, whereas standard ensembling can arbitrarily affect the bias. Empirically, standard ensembling reducesthe bias, leading us to hypothesize that ensembles of classifiers may perform well in part because of this unexpected reduction.We conclude by an empirical analysis of recent deep learning methods that ensemble over hyperparameters, revealing that these techniques indeed favor bias reduction. This suggests that, contrary to classical wisdom, targeting bias reduction may be a promising direction for classifier ensembles.

Understanding the bias-variance tradeoff of Bregman divergences

This paper builds upon the work of Pfau (2013), which generalized the bias variance tradeoff to any Bregman divergence loss function. Pfau (2013) showed that for Bregman divergences, the bias and variances are defined with respect to a central label, defined as the mean of the label variable, and a central prediction, of a more complex form. We show that, similarly to the label, the central prediction can be interpreted as the mean of a random variable, where the mean operates in a dual space defined by the loss function itself. Viewing the bias-variance tradeoff through operations taken in dual space, we subsequently derive several results of interest. In particular, (a) the variance terms satisfy a generalized law of total variance; (b) if a source of randomness cannot be controlled, its contribution to the bias and variance has a closed form; (c) there exist natural ensembling operations in the label and prediction spaces which reduce the variance and do not affect the bias.

Scalable and Flexible Deep Bayesian Optimization with Auxiliary Information for Scientific Problems

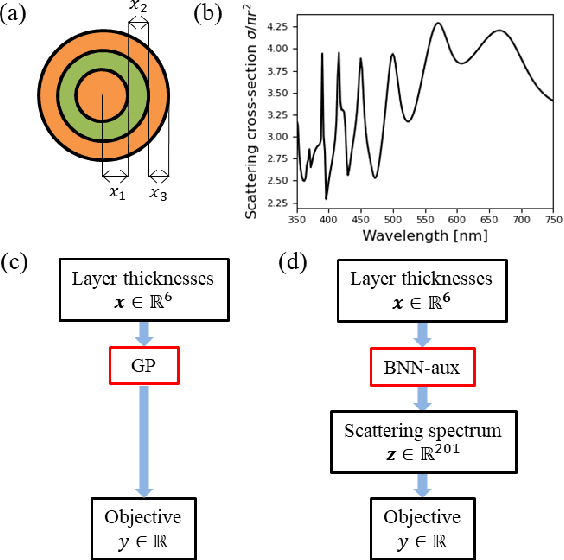
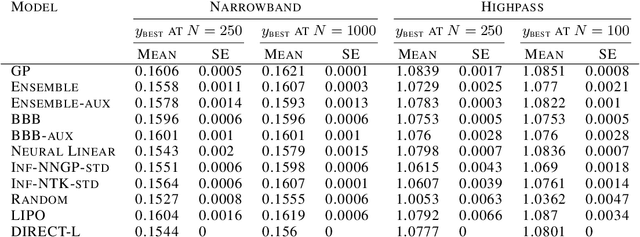
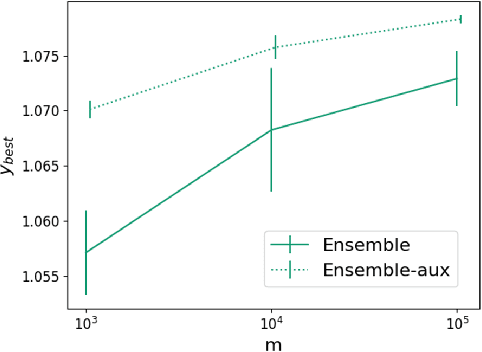
Bayesian optimization (BO) is a popular paradigm for global optimization of expensive black-box functions, but there are many domains where the function is not completely black-box. The data may have some known structure, e.g. symmetries, and the data generation process can yield useful intermediate or auxiliary information in addition to the value of the optimization objective. However, surrogate models traditionally employed in BO, such as Gaussian Processes (GPs), scale poorly with dataset size and struggle to incorporate known structure or auxiliary information. Instead, we propose performing BO on complex, structured problems by using Bayesian Neural Networks (BNNs), a class of scalable surrogate models that have the representation power and flexibility to handle structured data and exploit auxiliary information. We demonstrate BO on a number of realistic problems in physics and chemistry, including topology optimization of photonic crystal materials using convolutional neural networks, and chemical property optimization of molecules using graph neural networks. On these complex tasks, we show that BNNs often outperform GPs as surrogate models for BO in terms of both sampling efficiency and computational cost.

Estimating the Spectral Density of Large Implicit Matrices

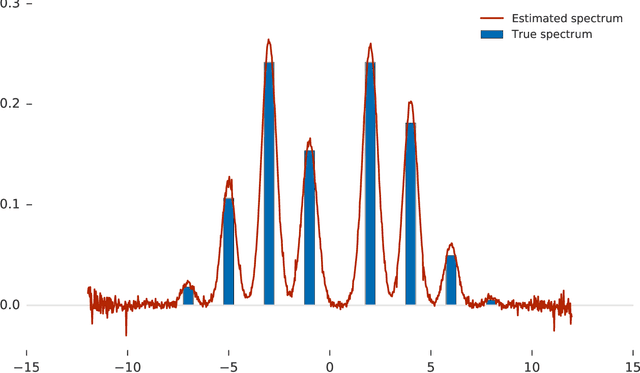
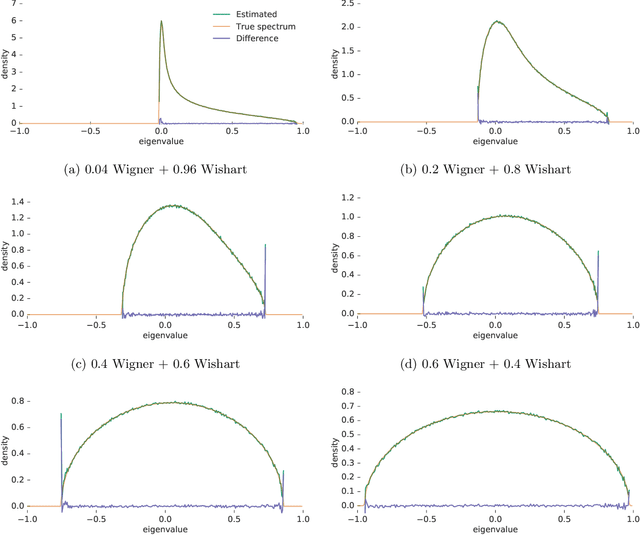
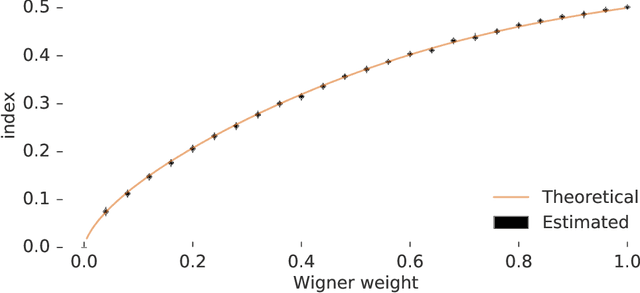
Many important problems are characterized by the eigenvalues of a large matrix. For example, the difficulty of many optimization problems, such as those arising from the fitting of large models in statistics and machine learning, can be investigated via the spectrum of the Hessian of the empirical loss function. Network data can be understood via the eigenstructure of a graph Laplacian matrix using spectral graph theory. Quantum simulations and other many-body problems are often characterized via the eigenvalues of the solution space, as are various dynamic systems. However, naive eigenvalue estimation is computationally expensive even when the matrix can be represented; in many of these situations the matrix is so large as to only be available implicitly via products with vectors. Even worse, one may only have noisy estimates of such matrix vector products. In this work, we combine several different techniques for randomized estimation and show that it is possible to construct unbiased estimators to answer a broad class of questions about the spectra of such implicit matrices, even in the presence of noise. We validate these methods on large-scale problems in which graph theory and random matrix theory provide ground truth.

TensorFlow Estimators: Managing Simplicity vs. Flexibility in High-Level Machine Learning Frameworks

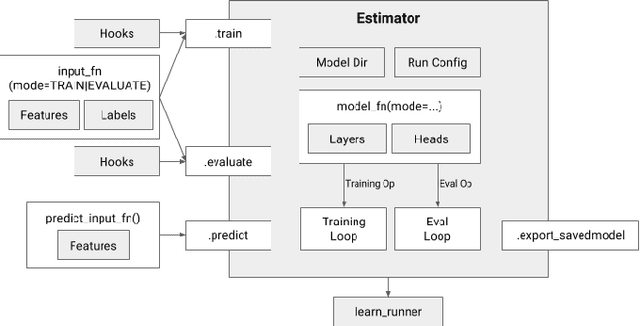
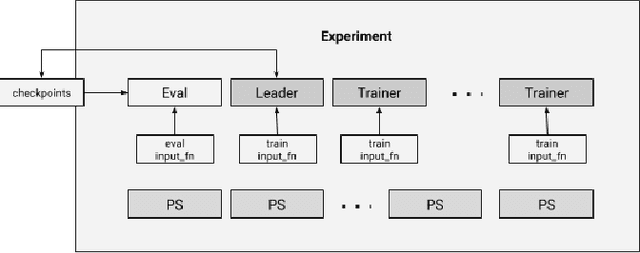
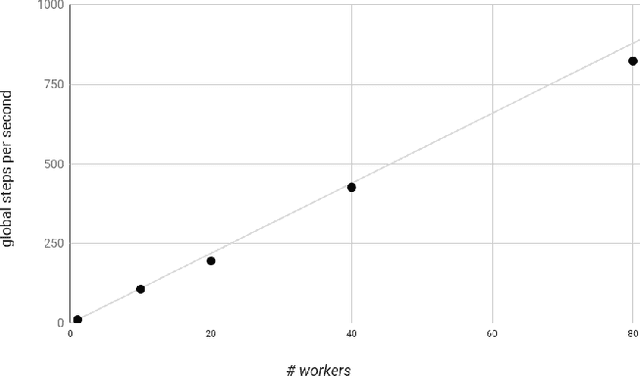
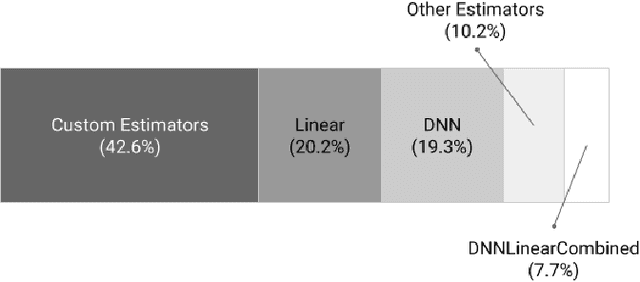
We present a framework for specifying, training, evaluating, and deploying machine learning models. Our focus is on simplifying cutting edge machine learning for practitioners in order to bring such technologies into production. Recognizing the fast evolution of the field of deep learning, we make no attempt to capture the design space of all possible model architectures in a domain- specific language (DSL) or similar configuration language. We allow users to write code to define their models, but provide abstractions that guide develop- ers to write models in ways conducive to productionization. We also provide a unifying Estimator interface, making it possible to write downstream infrastructure (e.g. distributed training, hyperparameter tuning) independent of the model implementation. We balance the competing demands for flexibility and simplicity by offering APIs at different levels of abstraction, making common model architectures available out of the box, while providing a library of utilities designed to speed up experimentation with model architectures. To make out of the box models flexible and usable across a wide range of problems, these canned Estimators are parameterized not only over traditional hyperparameters, but also using feature columns, a declarative specification describing how to interpret input data. We discuss our experience in using this framework in re- search and production environments, and show the impact on code health, maintainability, and development speed.