ContextMRI: Enhancing Compressed Sensing MRI through Metadata Conditioning

Compressed sensing MRI seeks to accelerate MRI acquisition processes by sampling fewer k-space measurements and then reconstructing the missing data algorithmically. The success of these approaches often relies on strong priors or learned statistical models. While recent diffusion model-based priors have shown great potential, previous methods typically ignore clinically available metadata (e.g. patient demographics, imaging parameters, slice-specific information). In practice, metadata contains meaningful cues about the anatomy and acquisition protocol, suggesting it could further constrain the reconstruction problem. In this work, we propose ContextMRI, a text-conditioned diffusion model for MRI that integrates granular metadata into the reconstruction process. We train a pixel-space diffusion model directly on minimally processed, complex-valued MRI images. During inference, metadata is converted into a structured text prompt and fed to the model via CLIP text embeddings. By conditioning the prior on metadata, we unlock more accurate reconstructions and show consistent gains across multiple datasets, acceleration factors, and undersampling patterns. Our experiments demonstrate that increasing the fidelity of metadata, ranging from slice location and contrast to patient age, sex, and pathology, systematically boosts reconstruction performance. This work highlights the untapped potential of leveraging clinical context for inverse problems and opens a new direction for metadata-driven MRI reconstruction.

Exoplanet Detection via Differentiable Rendering

Direct imaging of exoplanets is crucial for advancing our understanding of planetary systems beyond our solar system, but it faces significant challenges due to the high contrast between host stars and their planets. Wavefront aberrations introduce speckles in the telescope science images, which are patterns of diffracted starlight that can mimic the appearance of planets, complicating the detection of faint exoplanet signals. Traditional post-processing methods, operating primarily in the image intensity domain, do not integrate wavefront sensing data. These data, measured mainly for adaptive optics corrections, have been overlooked as a potential resource for post-processing, partly due to the challenge of the evolving nature of wavefront aberrations. In this paper, we present a differentiable rendering approach that leverages these wavefront sensing data to improve exoplanet detection. Our differentiable renderer models wave-based light propagation through a coronagraphic telescope system, allowing gradient-based optimization to significantly improve starlight subtraction and increase sensitivity to faint exoplanets. Simulation experiments based on the James Webb Space Telescope configuration demonstrate the effectiveness of our approach, achieving substantial improvements in contrast and planet detection limits. Our results showcase how the computational advancements enabled by differentiable rendering can revitalize previously underexploited wavefront data, opening new avenues for enhancing exoplanet imaging and characterization.

Neural Approximate Mirror Maps for Constrained Diffusion Models

Diffusion models excel at creating visually-convincing images, but they often struggle to meet subtle constraints inherent in the training data. Such constraints could be physics-based (e.g., satisfying a PDE), geometric (e.g., respecting symmetry), or semantic (e.g., including a particular number of objects). When the training data all satisfy a certain constraint, enforcing this constraint on a diffusion model not only improves its distribution-matching accuracy but also makes it more reliable for generating valid synthetic data and solving constrained inverse problems. However, existing methods for constrained diffusion models are inflexible with different types of constraints. Recent work proposed to learn mirror diffusion models (MDMs) in an unconstrained space defined by a mirror map and to impose the constraint with an inverse mirror map, but analytical mirror maps are challenging to derive for complex constraints. We propose neural approximate mirror maps (NAMMs) for general constraints. Our approach only requires a differentiable distance function from the constraint set. We learn an approximate mirror map that pushes data into an unconstrained space and a corresponding approximate inverse that maps data back to the constraint set. A generative model, such as an MDM, can then be trained in the learned mirror space and its samples restored to the constraint set by the inverse map. We validate our approach on a variety of constraints, showing that compared to an unconstrained diffusion model, a NAMM-based MDM substantially improves constraint satisfaction. We also demonstrate how existing diffusion-based inverse-problem solvers can be easily applied in the learned mirror space to solve constrained inverse problems.

Event-horizon-scale Imaging of M87* under Different Assumptions via Deep Generative Image Priors

Reconstructing images from the Event Horizon Telescope (EHT) observations of M87*, the supermassive black hole at the center of the galaxy M87, depends on a prior to impose desired image statistics. However, given the impossibility of directly observing black holes, there is no clear choice for a prior. We present a framework for flexibly designing a range of priors, each bringing different biases to the image reconstruction. These priors can be weak (e.g., impose only basic natural-image statistics) or strong (e.g., impose assumptions of black-hole structure). Our framework uses Bayesian inference with score-based priors, which are data-driven priors arising from a deep generative model that can learn complicated image distributions. Using our Bayesian imaging approach with sophisticated data-driven priors, we can assess how visual features and uncertainty of reconstructed images change depending on the prior. In addition to simulated data, we image the real EHT M87* data and discuss how recovered features are influenced by the choice of prior.

Principled Probabilistic Imaging using Diffusion Models as Plug-and-Play Priors

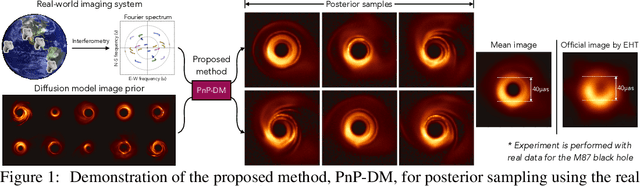
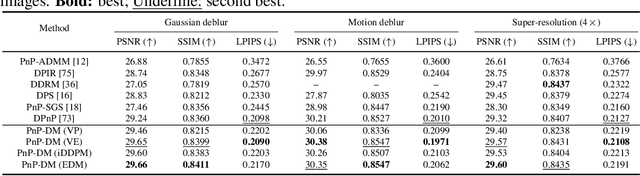
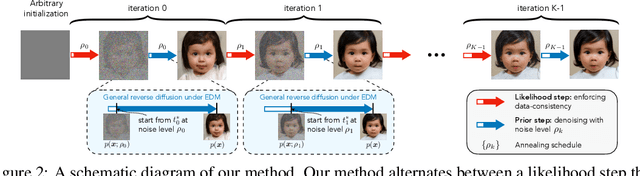
Diffusion models (DMs) have recently shown outstanding capability in modeling complex image distributions, making them expressive image priors for solving Bayesian inverse problems. However, most existing DM-based methods rely on approximations in the generative process to be generic to different inverse problems, leading to inaccurate sample distributions that deviate from the target posterior defined within the Bayesian framework. To harness the generative power of DMs while avoiding such approximations, we propose a Markov chain Monte Carlo algorithm that performs posterior sampling for general inverse problems by reducing it to sampling the posterior of a Gaussian denoising problem. Crucially, we leverage a general DM formulation as a unified interface that allows for rigorously solving the denoising problem with a range of state-of-the-art DMs. We demonstrate the effectiveness of the proposed method on six inverse problems (three linear and three nonlinear), including a real-world black hole imaging problem. Experimental results indicate that our proposed method offers more accurate reconstructions and posterior estimation compared to existing DM-based imaging inverse methods.

Score-Based Diffusion Models for Photoacoustic Tomography Image Reconstruction

Photoacoustic tomography (PAT) is a rapidly-evolving medical imaging modality that combines optical absorption contrast with ultrasound imaging depth. One challenge in PAT is image reconstruction with inadequate acoustic signals due to limited sensor coverage or due to the density of the transducer array. Such cases call for solving an ill-posed inverse reconstruction problem. In this work, we use score-based diffusion models to solve the inverse problem of reconstructing an image from limited PAT measurements. The proposed approach allows us to incorporate an expressive prior learned by a diffusion model on simulated vessel structures while still being robust to varying transducer sparsity conditions.

Provable Probabilistic Imaging using Score-Based Generative Priors

Estimating high-quality images while also quantifying their uncertainty are two desired features in an image reconstruction algorithm for solving ill-posed inverse problems. In this paper, we propose plug-and-play Monte Carlo (PMC) as a principled framework for characterizing the space of possible solutions to a general inverse problem. PMC is able to incorporate expressive score-based generative priors for high-quality image reconstruction while also performing uncertainty quantification via posterior sampling. In particular, we introduce two PMC algorithms which can be viewed as the sampling analogues of the traditional plug-and-play priors (PnP) and regularization by denoising (RED) algorithms. We also establish a theoretical analysis for characterizing the convergence of the PMC algorithms. Our analysis provides non-asymptotic stationarity guarantees for both algorithms, even in the presence of non-log-concave likelihoods and imperfect score networks. We demonstrate the performance of the PMC algorithms on multiple representative inverse problems with both linear and nonlinear forward models. Experimental results show that PMC significantly improves reconstruction quality and enables high-fidelity uncertainty quantification.

Orbital Polarimetric Tomography of a Flare Near the Sagittarius A* Supermassive Black Hole

The interaction between the supermassive black hole at the center of the Milky Way, Sagittarius A$^*$, and its accretion disk, occasionally produces high energy flares seen in X-ray, infrared and radio. One mechanism for observed flares is the formation of compact bright regions that appear within the accretion disk and close to the event horizon. Understanding these flares can provide a window into black hole accretion processes. Although sophisticated simulations predict the formation of these flares, their structure has yet to be recovered by observations. Here we show the first three-dimensional (3D) reconstruction of an emission flare in orbit recovered from ALMA light curves observed on April 11, 2017. Our recovery results show compact bright regions at a distance of roughly 6 times the event horizon. Moreover, our recovery suggests a clockwise rotation in a low-inclination orbital plane, a result consistent with prior studies by EHT and GRAVITY collaborations. To recover this emission structure we solve a highly ill-posed tomography problem by integrating a neural 3D representation (an emergent artificial intelligence approach for 3D reconstruction) with a gravitational model for black holes. Although the recovered 3D structure is subject, and sometimes sensitive, to the model assumptions, under physically motivated choices we find that our results are stable and our approach is successful on simulated data. We anticipate that in the future, this approach could be used to analyze a richer collection of time-series data that could shed light on the mechanisms governing black hole and plasma dynamics.

Single View Refractive Index Tomography with Neural Fields

Refractive Index Tomography is an inverse problem in which we seek to reconstruct a scene's 3D refractive field from 2D projected image measurements. The refractive field is not visible itself, but instead affects how the path of a light ray is continuously curved as it travels through space. Refractive fields appear across a wide variety of scientific applications, from translucent cell samples in microscopy to fields of dark matter bending light from faraway galaxies. This problem poses a unique challenge because the refractive field directly affects the path that light takes, making its recovery a non-linear problem. In addition, in contrast with traditional tomography, we seek to recover the refractive field using a projected image from only a single viewpoint by leveraging knowledge of light sources scattered throughout the medium. In this work, we introduce a method that uses a coordinate-based neural network to model the underlying continuous refractive field in a scene. We then use explicit modeling of rays' 3D spatial curvature to optimize the parameters of this network, reconstructing refractive fields with an analysis-by-synthesis approach. The efficacy of our approach is demonstrated by recovering refractive fields in simulation, and analyzing how recovery is affected by the light source distribution. We then test our method on a simulated dark matter mapping problem, where we recover the refractive field underlying a realistic simulated dark matter distribution.

Efficient Bayesian Computational Imaging with a Surrogate Score-Based Prior

We propose a surrogate function for efficient use of score-based priors for Bayesian inverse imaging. Recent work turned score-based diffusion models into probabilistic priors for solving ill-posed imaging problems by appealing to an ODE-based log-probability function. However, evaluating this function is computationally inefficient and inhibits posterior estimation of high-dimensional images. Our proposed surrogate prior is based on the evidence lower-bound of a score-based diffusion model. We demonstrate the surrogate prior on variational inference for efficient approximate posterior sampling of large images. Compared to the exact prior in previous work, our surrogate prior accelerates optimization of the variational image distribution by at least two orders of magnitude. We also find that our principled approach achieves higher-fidelity images than non-Bayesian baselines that involve hyperparameter-tuning at inference. Our work establishes a practical path forward for using score-based diffusion models as general-purpose priors for imaging.