Zachary E. Ross
Ambient Noise Full Waveform Inversion with Neural Operators
Mar 19, 2025Abstract:Numerical simulations of seismic wave propagation are crucial for investigating velocity structures and improving seismic hazard assessment. However, standard methods such as finite difference or finite element are computationally expensive. Recent studies have shown that a new class of machine learning models, called neural operators, can solve the elastodynamic wave equation orders of magnitude faster than conventional methods. Full waveform inversion is a prime beneficiary of the accelerated simulations. Neural operators, as end-to-end differentiable operators, combined with automatic differentiation, provide an alternative approach to the adjoint-state method. Since neural operators do not involve the Born approximation, when used for full waveform inversion they have the potential to include additional phases and alleviate cycle-skipping problems present in traditional adjoint-state formulations. In this study, we demonstrate the application of neural operators for full waveform inversion on a real seismic dataset, which consists of several nodal transects collected across the San Gabriel, Chino, and San Bernardino basins in the Los Angeles metropolitan area.
InverseBench: Benchmarking Plug-and-Play Diffusion Priors for Inverse Problems in Physical Sciences
Mar 14, 2025



Abstract:Plug-and-play diffusion priors (PnPDP) have emerged as a promising research direction for solving inverse problems. However, current studies primarily focus on natural image restoration, leaving the performance of these algorithms in scientific inverse problems largely unexplored. To address this gap, we introduce \textsc{InverseBench}, a framework that evaluates diffusion models across five distinct scientific inverse problems. These problems present unique structural challenges that differ from existing benchmarks, arising from critical scientific applications such as optical tomography, medical imaging, black hole imaging, seismology, and fluid dynamics. With \textsc{InverseBench}, we benchmark 14 inverse problem algorithms that use plug-and-play diffusion priors against strong, domain-specific baselines, offering valuable new insights into the strengths and weaknesses of existing algorithms. To facilitate further research and development, we open-source the codebase, along with datasets and pre-trained models, at https://devzhk.github.io/InverseBench/.
Stochastic Process Learning via Operator Flow Matching
Jan 07, 2025
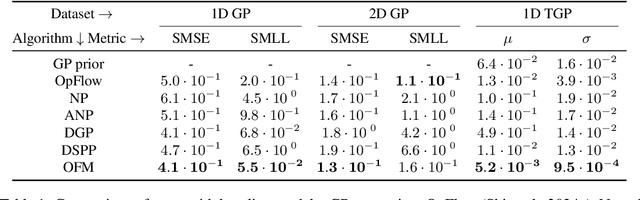
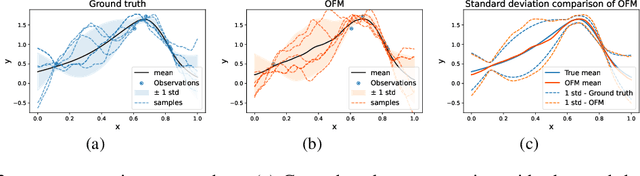
Abstract:Expanding on neural operators, we propose a novel framework for stochastic process learning across arbitrary domains. In particular, we develop operator flow matching (\alg) for learning stochastic process priors on function spaces. \alg provides the probability density of the values of any collection of points and enables mathematically tractable functional regression at new points with mean and density estimation. Our method outperforms state-of-the-art models in stochastic process learning, functional regression, and prior learning.
Universal Functional Regression with Neural Operator Flows
Apr 03, 2024Abstract:Regression on function spaces is typically limited to models with Gaussian process priors. We introduce the notion of universal functional regression, in which we aim to learn a prior distribution over non-Gaussian function spaces that remains mathematically tractable for functional regression. To do this, we develop Neural Operator Flows (OpFlow), an infinite-dimensional extension of normalizing flows. OpFlow is an invertible operator that maps the (potentially unknown) data function space into a Gaussian process, allowing for exact likelihood estimation of functional point evaluations. OpFlow enables robust and accurate uncertainty quantification via drawing posterior samples of the Gaussian process and subsequently mapping them into the data function space. We empirically study the performance of OpFlow on regression and generation tasks with data generated from Gaussian processes with known posterior forms and non-Gaussian processes, as well as real-world earthquake seismograms with an unknown closed-form distribution.
Broadband Ground Motion Synthesis via Generative Adversarial Neural Operators: Development and Validation
Sep 07, 2023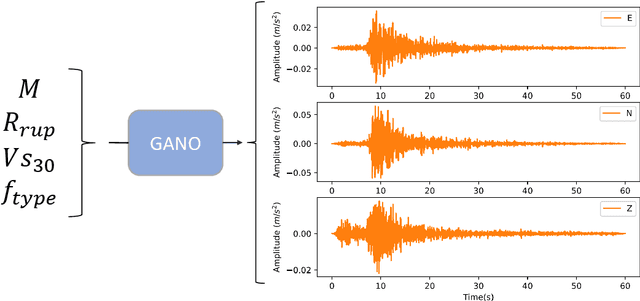
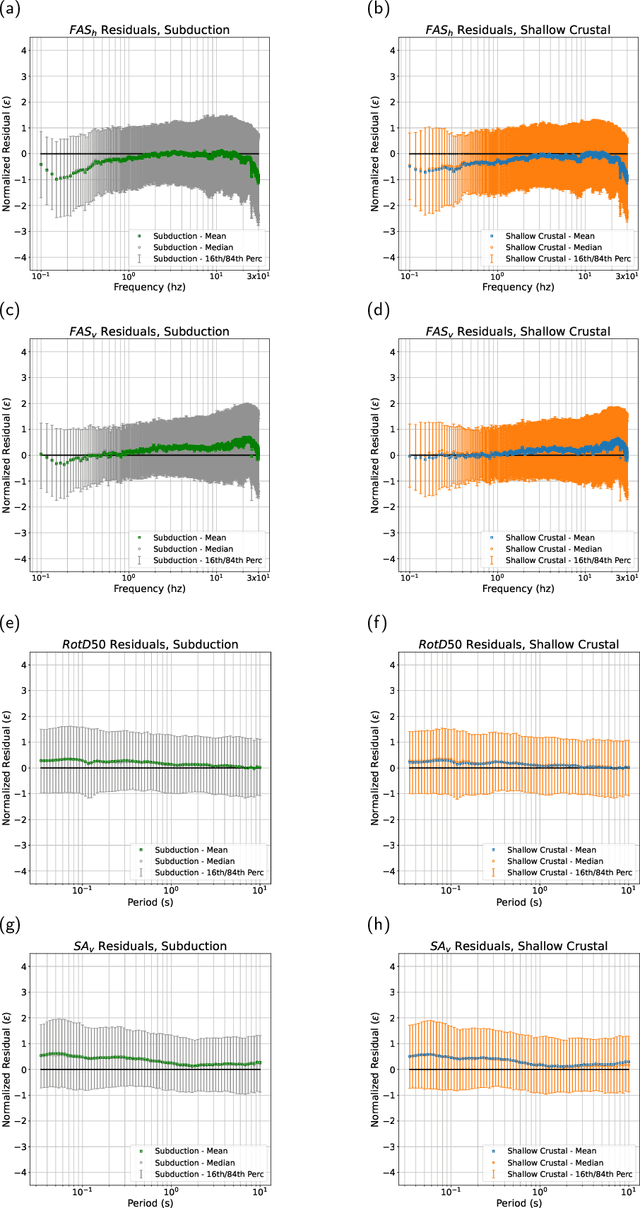
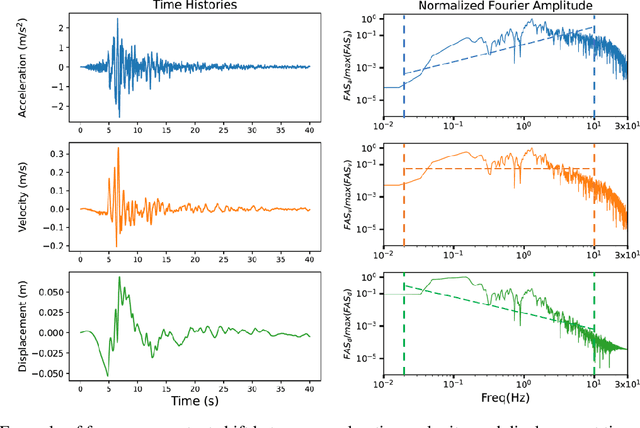
Abstract:We present a data-driven model for ground-motion synthesis using a Generative Adversarial Neural Operator (GANO) that combines recent advancements in machine learning and open access strong motion data sets to generate three-component acceleration time histories conditioned on moment magnitude ($M$), rupture distance ($R_{rup}$), time-average shear-wave velocity at the top $30m$ ($V_{S30}$), and tectonic environment or style of faulting. We use Neural Operators, a resolution invariant architecture that guarantees that the model training is independent of the data sampling frequency. We first present the conditional ground-motion synthesis algorithm (referred to heretofore as cGM-GANO) and discuss its advantages compared to previous work. Next, we verify the cGM-GANO framework using simulated ground motions generated with the Southern California Earthquake Center (SCEC) Broadband Platform (BBP). We lastly train cGM-GANO on a KiK-net dataset from Japan, showing that the framework can recover the magnitude, distance, and $V_{S30}$ scaling of Fourier amplitude and pseudo-spectral accelerations. We evaluate cGM-GANO through residual analysis with the empirical dataset as well as by comparison with conventional Ground Motion Models (GMMs) for selected ground motion scenarios. Results show that cGM-GANO produces consistent median scaling with the GMMs for the corresponding tectonic environments. The largest misfit is observed at short distances due to the scarcity of training data. With the exception of short distances, the aleatory variability of the response spectral ordinates is also well captured, especially for subduction events due to the adequacy of training data. Applications of the presented framework include generation of risk-targeted ground motions for site-specific engineering applications.
Generative Adversarial Neural Operators
May 06, 2022
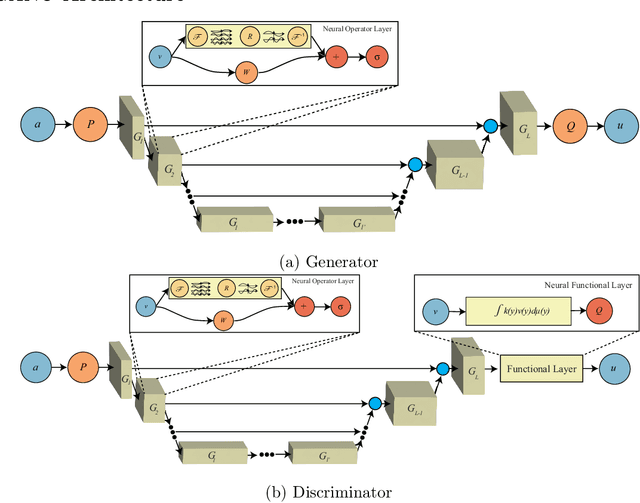

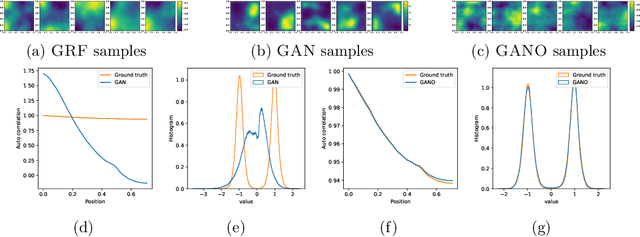
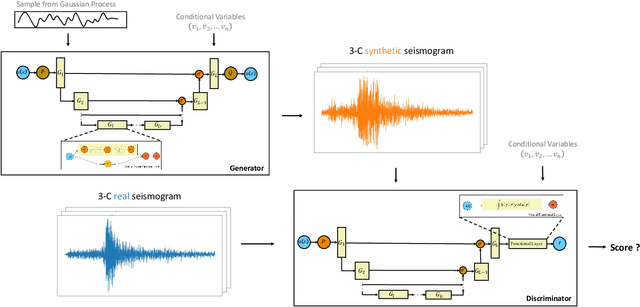
Abstract:We propose the generative adversarial neural operator (GANO), a generative model paradigm for learning probabilities on infinite-dimensional function spaces. The natural sciences and engineering are known to have many types of data that are sampled from infinite-dimensional function spaces, where classical finite-dimensional deep generative adversarial networks (GANs) may not be directly applicable. GANO generalizes the GAN framework and allows for the sampling of functions by learning push-forward operator maps in infinite-dimensional spaces. GANO consists of two main components, a generator neural operator and a discriminator neural functional. The inputs to the generator are samples of functions from a user-specified probability measure, e.g., Gaussian random field (GRF), and the generator outputs are synthetic data functions. The input to the discriminator is either a real or synthetic data function. In this work, we instantiate GANO using the Wasserstein criterion and show how the Wasserstein loss can be computed in infinite-dimensional spaces. We empirically study GANOs in controlled cases where both input and output functions are samples from GRFs and compare its performance to the finite-dimensional counterpart GAN. We empirically study the efficacy of GANO on real-world function data of volcanic activities and show its superior performance over GAN. Furthermore, we find that for the function-based data considered, GANOs are more stable to train than GANs and require less hyperparameter optimization.
U-NO: U-shaped Neural Operators
Apr 23, 2022


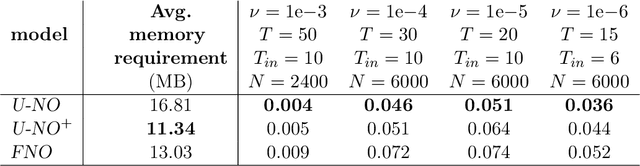
Abstract:Neural operators generalize classical neural networks to maps between infinite-dimensional spaces, e.g. function spaces. Prior works on neural operators proposed a series of novel architectures to learn such maps and demonstrated unprecedented success in solving partial differential equations (PDEs). In this paper, we propose U-shaped Neural Operators U-NO, an architecture that allows for deeper neural operators compared to prior works. U-NOs exploit the problems structures in function predictions, demonstrate fast training, data efficiency, and robustness w.r.t hyperparameters choices. We study the performance of U-NO on PDE benchmarks, namely, Darcy's flow law and the Navier-Stokes equations. We show that U-NO results in average of 14% and 38% prediction improvement on the Darcy's flow and Navier-Stokes equations, respectively, over the state of art.
Seismic wave propagation and inversion with Neural Operators
Aug 11, 2021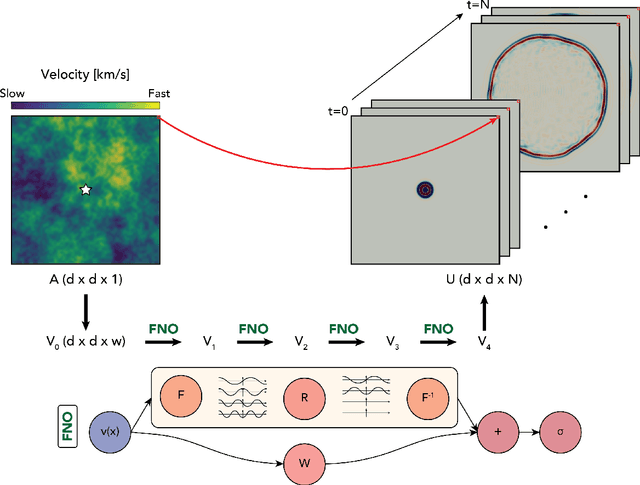
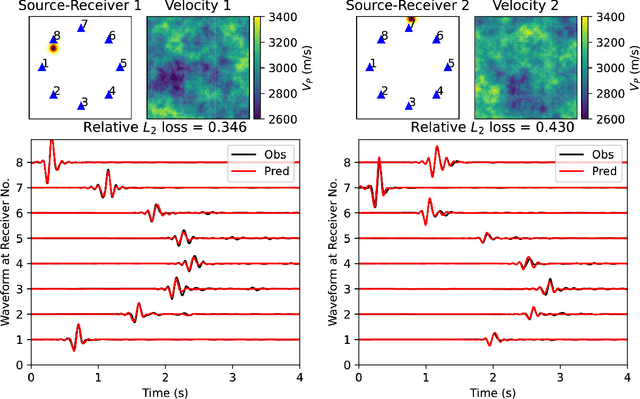
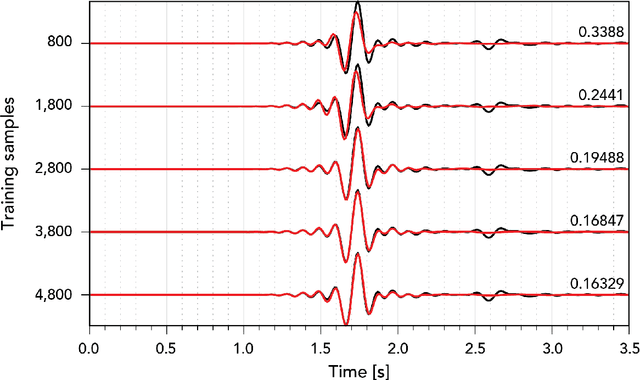
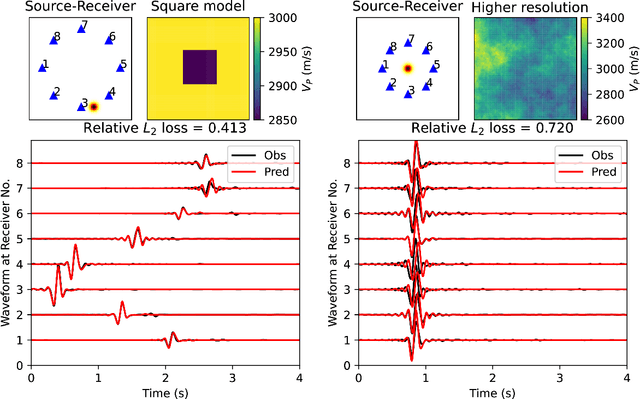
Abstract:Seismic wave propagation forms the basis for most aspects of seismological research, yet solving the wave equation is a major computational burden that inhibits the progress of research. This is exaspirated by the fact that new simulations must be performed when the velocity structure or source location is perturbed. Here, we explore a prototype framework for learning general solutions using a recently developed machine learning paradigm called Neural Operator. A trained Neural Operator can compute a solution in negligible time for any velocity structure or source location. We develop a scheme to train Neural Operators on an ensemble of simulations performed with random velocity models and source locations. As Neural Operators are grid-free, it is possible to evaluate solutions on higher resolution velocity models than trained on, providing additional computational efficiency. We illustrate the method with the 2D acoustic wave equation and demonstrate the method's applicability to seismic tomography, using reverse mode automatic differentiation to compute gradients of the wavefield with respect to the velocity structure. The developed procedure is nearly an order of magnitude faster than using conventional numerical methods for full waveform inversion.
Deep Learning-based Damage Mapping with InSAR Coherence Time Series
May 24, 2021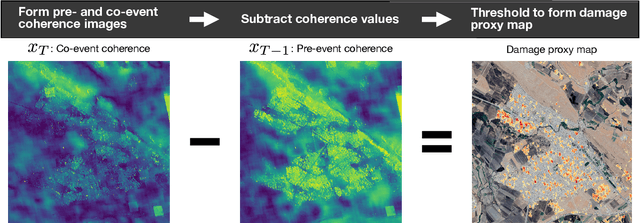
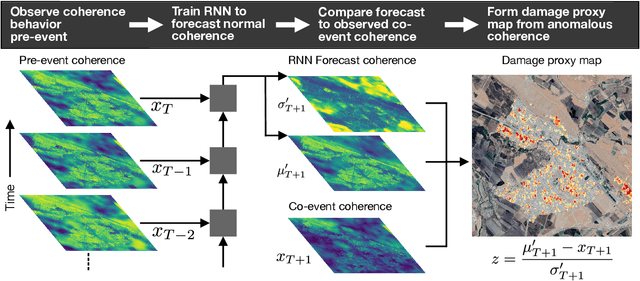
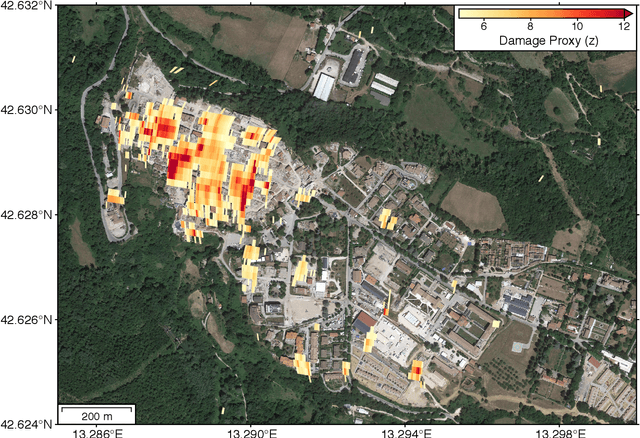
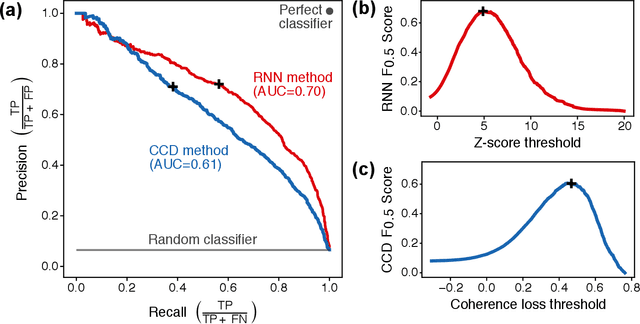
Abstract:Satellite remote sensing is playing an increasing role in the rapid mapping of damage after natural disasters. In particular, synthetic aperture radar (SAR) can image the Earth's surface and map damage in all weather conditions, day and night. However, current SAR damage mapping methods struggle to separate damage from other changes in the Earth's surface. In this study, we propose a novel approach to damage mapping, combining deep learning with the full time history of SAR observations of an impacted region in order to detect anomalous variations in the Earth's surface properties due to a natural disaster. We quantify Earth surface change using time series of Interferometric SAR coherence, then use a recurrent neural network (RNN) as a probabilistic anomaly detector on these coherence time series. The RNN is first trained on pre-event coherence time series, and then forecasts a probability distribution of the coherence between pre- and post-event SAR images. The difference between the forecast and observed co-event coherence provides a measure of the confidence in the identification of damage. The method allows the user to choose a damage detection threshold that is customized for each location, based on the local behavior of coherence through time before the event. We apply this method to calculate estimates of damage for three earthquakes using multi-year time series of Sentinel-1 SAR acquisitions. Our approach shows good agreement with observed damage and quantitative improvement compared to using pre- to co-event coherence loss as a damage proxy.
HypoSVI: Hypocenter inversion with Stein variational inference and Physics Informed Neural Networks
Jan 12, 2021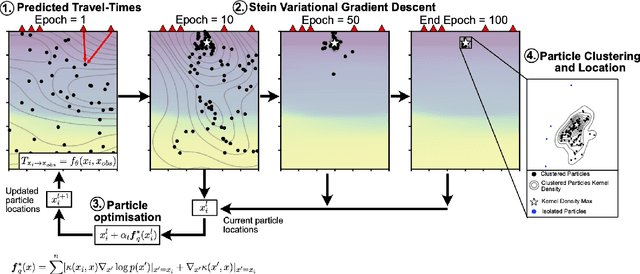
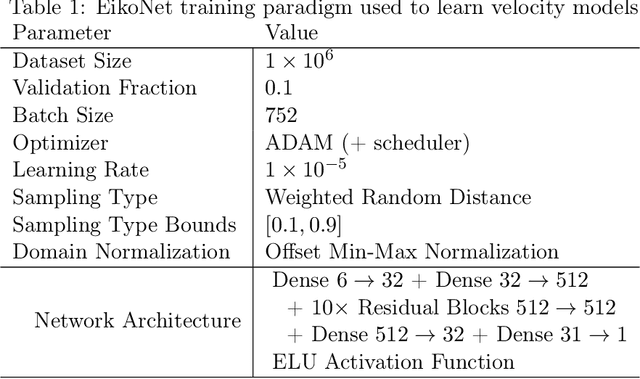
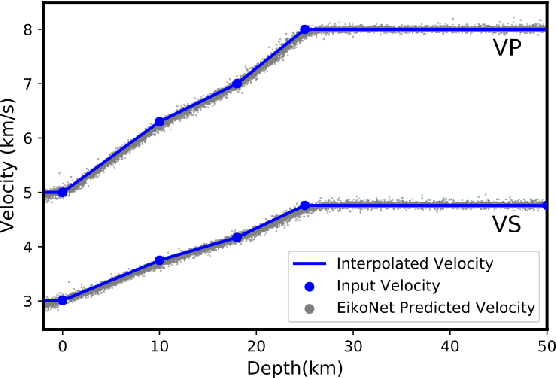
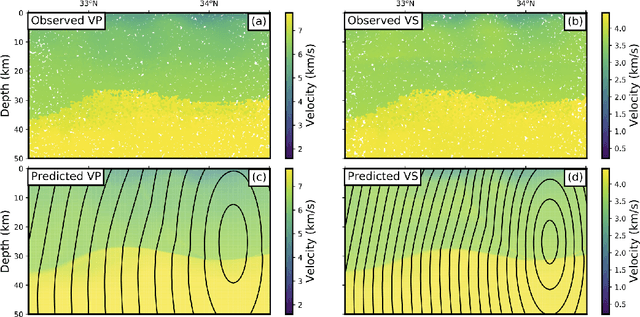
Abstract:We introduce a scheme for probabilistic hypocenter inversion with Stein variational inference. Our approach uses a differentiable forward model in the form of a physics-informed neural network, which we train to solve the Eikonal equation. This allows for rapid approximation of the posterior by iteratively optimizing a collection of particles against a kernelized Stein discrepancy. We show that the method is well-equipped to handle highly non-convex posterior distributions, which are common in hypocentral inverse problems. A suite of experiments is performed to examine the influence of the various hyperparameters. Once trained, the method is valid for any network geometry within the study area without the need to build travel time tables. We show that the computational demands scale efficiently with the number of differential times, making it ideal for large-N sensing technologies like Distributed Acoustic Sensing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge