Predicting the Geothermal Gradient in Colombia: a Machine Learning Approach

Accurate determination of the geothermal gradient is critical for assessing the geothermal energy potential of a given region. Of particular interest is the case of Colombia, a country with abundant geothermal resources. A history of active oil and gas exploration and production has left drilled boreholes in different geological settings, providing direct measurements of the geothermal gradient. Unfortunately, large regions of the country where geothermal resources might exist lack such measurements. Indirect geophysical measurements are costly and difficult to perform at regional scales. Computational thermal models could be constructed, but they require very detailed knowledge of the underlying geology and uniform sampling of subsurface temperatures to be well-constrained. We present an alternative approach that leverages recent advances in supervised machine learning and available direct measurements to predict the geothermal gradient in regions where only global-scale geophysical datasets and course geological knowledge are available. We find that a Gradient Boosted Regression Tree algorithm yields optimal predictions and extensively validate the trained model. We show that predictions of our model are within 12\% accuracy and that independent measurements performed by other authors agree well with our model. Finnally, we present a geothermal gradient map for Colombia that highlights regions where futher exploration and data collection should be performed.

Generative Adversarial Neural Operators

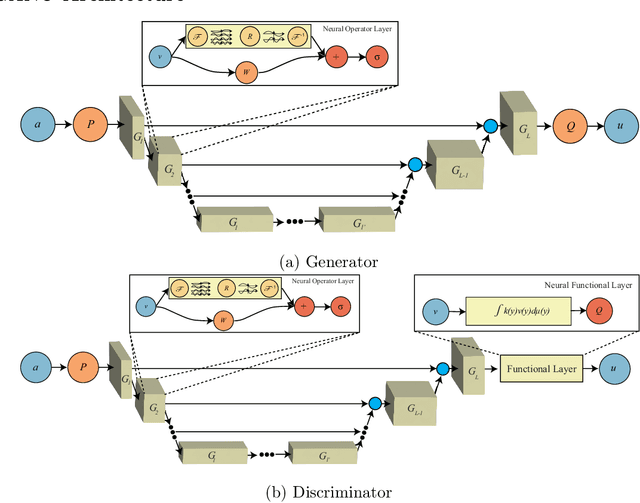
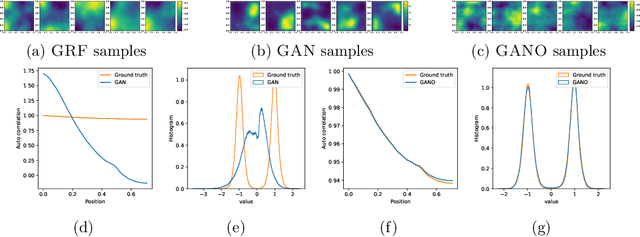
We propose the generative adversarial neural operator (GANO), a generative model paradigm for learning probabilities on infinite-dimensional function spaces. The natural sciences and engineering are known to have many types of data that are sampled from infinite-dimensional function spaces, where classical finite-dimensional deep generative adversarial networks (GANs) may not be directly applicable. GANO generalizes the GAN framework and allows for the sampling of functions by learning push-forward operator maps in infinite-dimensional spaces. GANO consists of two main components, a generator neural operator and a discriminator neural functional. The inputs to the generator are samples of functions from a user-specified probability measure, e.g., Gaussian random field (GRF), and the generator outputs are synthetic data functions. The input to the discriminator is either a real or synthetic data function. In this work, we instantiate GANO using the Wasserstein criterion and show how the Wasserstein loss can be computed in infinite-dimensional spaces. We empirically study GANOs in controlled cases where both input and output functions are samples from GRFs and compare its performance to the finite-dimensional counterpart GAN. We empirically study the efficacy of GANO on real-world function data of volcanic activities and show its superior performance over GAN. Furthermore, we find that for the function-based data considered, GANOs are more stable to train than GANs and require less hyperparameter optimization.

Data-driven Accelerogram Synthesis using Deep Generative Models

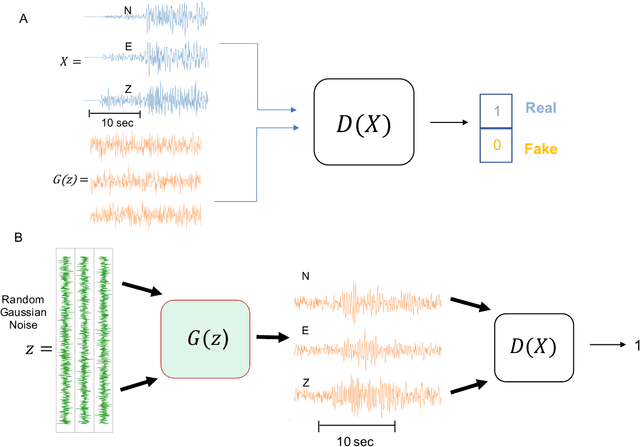
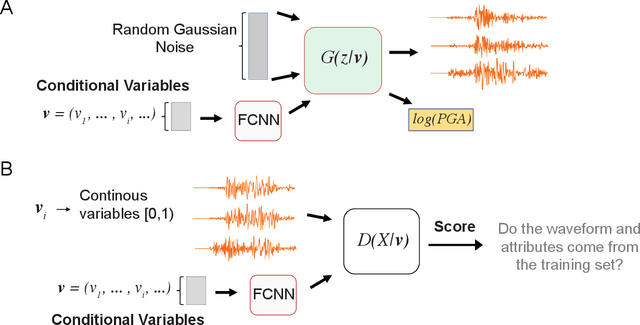
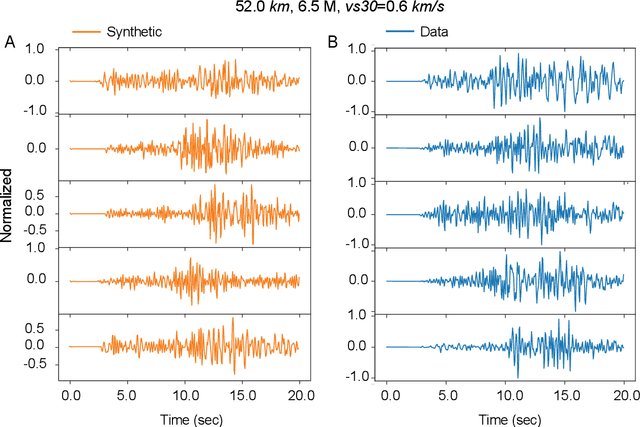
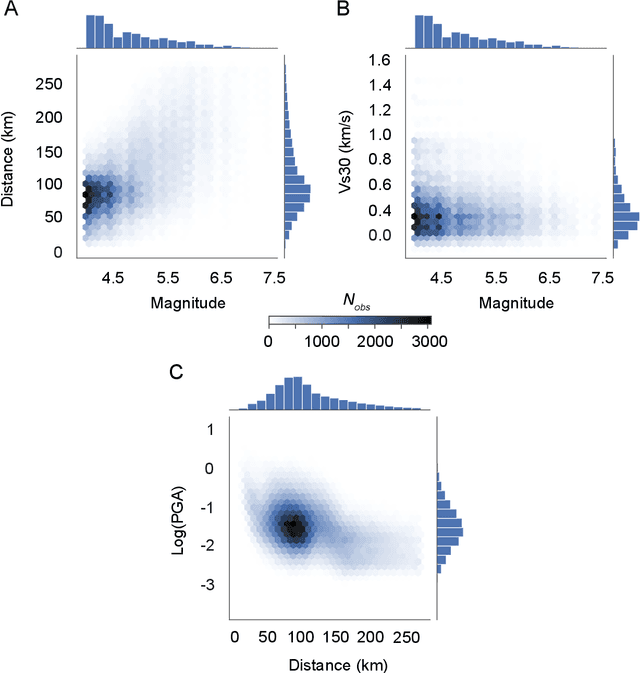
Robust estimation of ground motions generated by scenario earthquakes is critical for many engineering applications. We leverage recent advances in Generative Adversarial Networks (GANs) to develop a new framework for synthesizing earthquake acceleration time histories. Our approach extends the Wasserstein GAN formulation to allow for the generation of ground-motions conditioned on a set of continuous physical variables. Our model is trained to approximate the intrinsic probability distribution of a massive set of strong-motion recordings from Japan. We show that the trained generator model can synthesize realistic 3-Component accelerograms conditioned on magnitude, distance, and $V_{s30}$. Our model captures the expected statistical features of the acceleration spectra and waveform envelopes. The output seismograms display clear P and S-wave arrivals with the appropriate energy content and relative onset timing. The synthesized Peak Ground Acceleration (PGA) estimates are also consistent with observations. We develop a set of metrics that allow us to assess the training process's stability and tune model hyperparameters. We further show that the trained generator network can interpolate to conditions where no earthquake ground motion recordings exist. Our approach allows the on-demand synthesis of accelerograms for engineering purposes.