Domniki Asimaki
Stochastic Process Learning via Operator Flow Matching
Jan 07, 2025
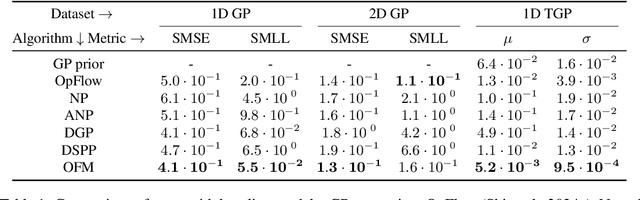
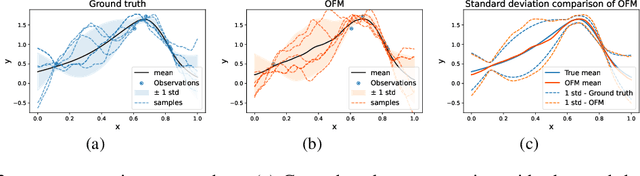
Abstract:Expanding on neural operators, we propose a novel framework for stochastic process learning across arbitrary domains. In particular, we develop operator flow matching (\alg) for learning stochastic process priors on function spaces. \alg provides the probability density of the values of any collection of points and enables mathematically tractable functional regression at new points with mean and density estimation. Our method outperforms state-of-the-art models in stochastic process learning, functional regression, and prior learning.
Broadband Ground Motion Synthesis via Generative Adversarial Neural Operators: Development and Validation
Sep 07, 2023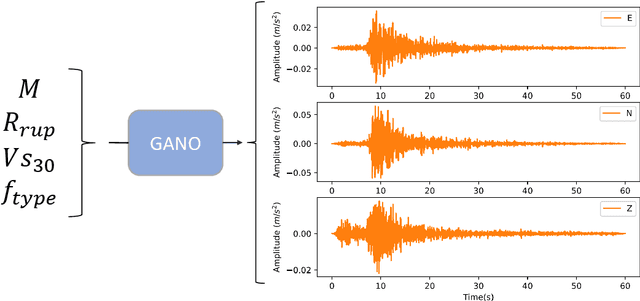
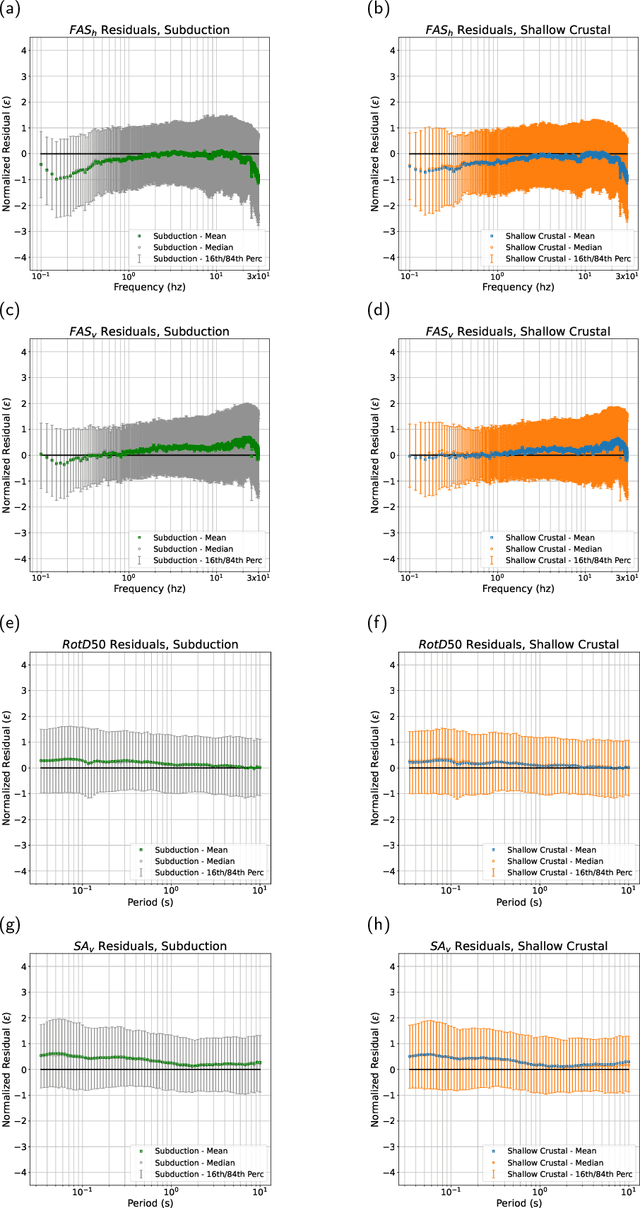
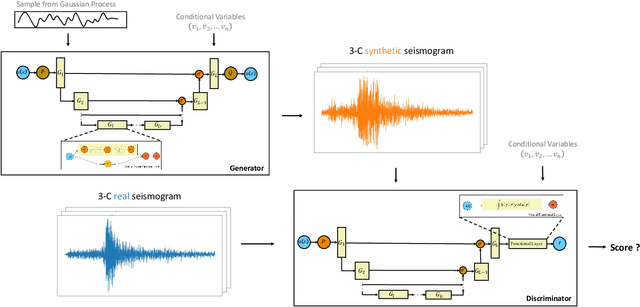
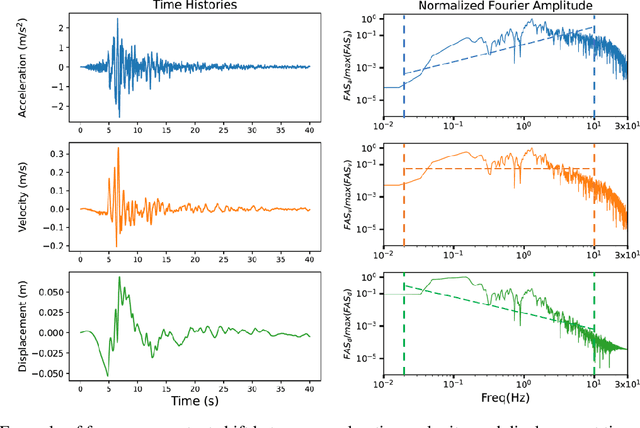
Abstract:We present a data-driven model for ground-motion synthesis using a Generative Adversarial Neural Operator (GANO) that combines recent advancements in machine learning and open access strong motion data sets to generate three-component acceleration time histories conditioned on moment magnitude ($M$), rupture distance ($R_{rup}$), time-average shear-wave velocity at the top $30m$ ($V_{S30}$), and tectonic environment or style of faulting. We use Neural Operators, a resolution invariant architecture that guarantees that the model training is independent of the data sampling frequency. We first present the conditional ground-motion synthesis algorithm (referred to heretofore as cGM-GANO) and discuss its advantages compared to previous work. Next, we verify the cGM-GANO framework using simulated ground motions generated with the Southern California Earthquake Center (SCEC) Broadband Platform (BBP). We lastly train cGM-GANO on a KiK-net dataset from Japan, showing that the framework can recover the magnitude, distance, and $V_{S30}$ scaling of Fourier amplitude and pseudo-spectral accelerations. We evaluate cGM-GANO through residual analysis with the empirical dataset as well as by comparison with conventional Ground Motion Models (GMMs) for selected ground motion scenarios. Results show that cGM-GANO produces consistent median scaling with the GMMs for the corresponding tectonic environments. The largest misfit is observed at short distances due to the scarcity of training data. With the exception of short distances, the aleatory variability of the response spectral ordinates is also well captured, especially for subduction events due to the adequacy of training data. Applications of the presented framework include generation of risk-targeted ground motions for site-specific engineering applications.
Data-driven Accelerogram Synthesis using Deep Generative Models
Nov 18, 2020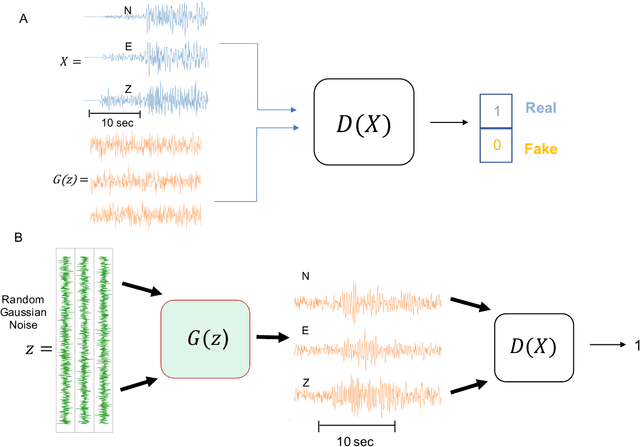
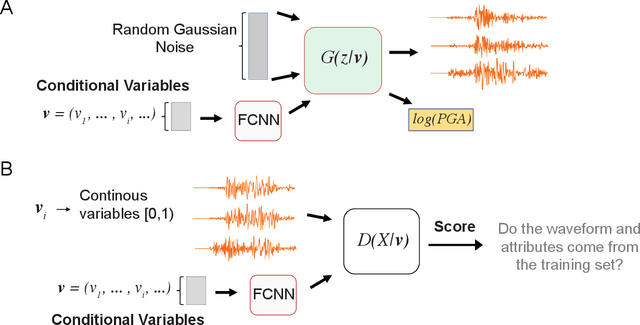
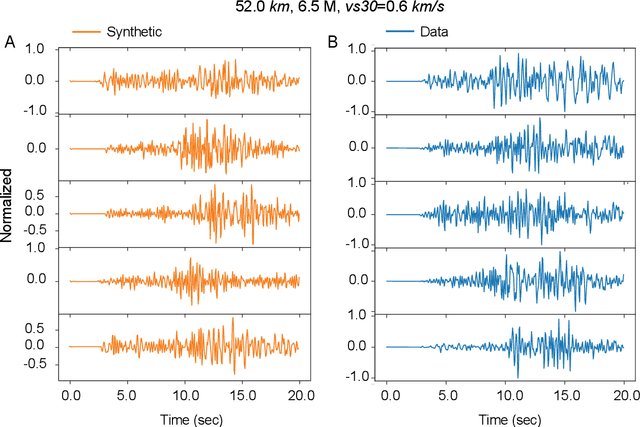
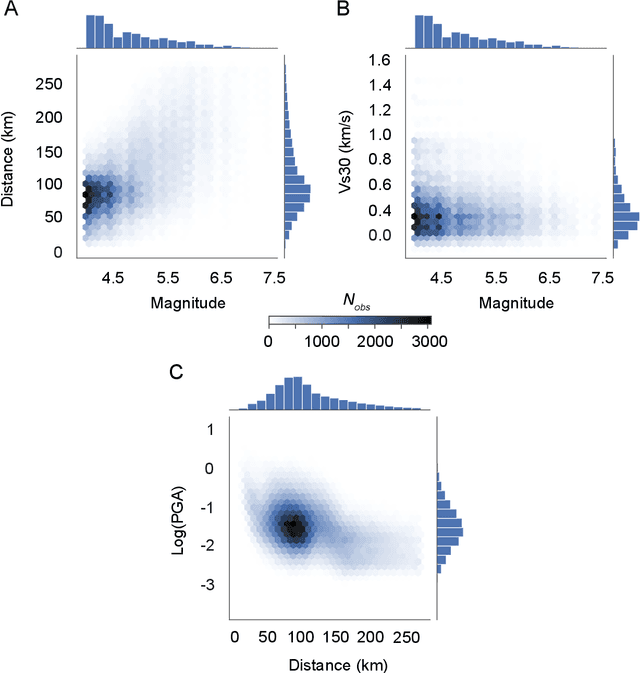
Abstract:Robust estimation of ground motions generated by scenario earthquakes is critical for many engineering applications. We leverage recent advances in Generative Adversarial Networks (GANs) to develop a new framework for synthesizing earthquake acceleration time histories. Our approach extends the Wasserstein GAN formulation to allow for the generation of ground-motions conditioned on a set of continuous physical variables. Our model is trained to approximate the intrinsic probability distribution of a massive set of strong-motion recordings from Japan. We show that the trained generator model can synthesize realistic 3-Component accelerograms conditioned on magnitude, distance, and $V_{s30}$. Our model captures the expected statistical features of the acceleration spectra and waveform envelopes. The output seismograms display clear P and S-wave arrivals with the appropriate energy content and relative onset timing. The synthesized Peak Ground Acceleration (PGA) estimates are also consistent with observations. We develop a set of metrics that allow us to assess the training process's stability and tune model hyperparameters. We further show that the trained generator network can interpolate to conditions where no earthquake ground motion recordings exist. Our approach allows the on-demand synthesis of accelerograms for engineering purposes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge