Stochastic Process Learning via Operator Flow Matching
Paper and Code
Jan 07, 2025
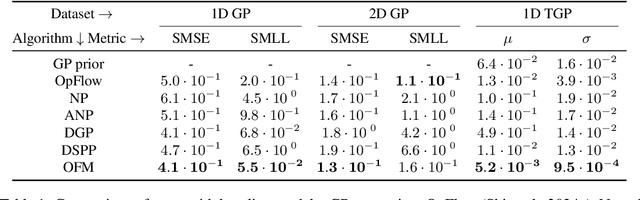
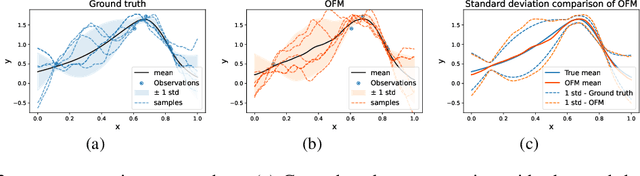
Expanding on neural operators, we propose a novel framework for stochastic process learning across arbitrary domains. In particular, we develop operator flow matching (\alg) for learning stochastic process priors on function spaces. \alg provides the probability density of the values of any collection of points and enables mathematically tractable functional regression at new points with mean and density estimation. Our method outperforms state-of-the-art models in stochastic process learning, functional regression, and prior learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge