Principled Approaches for Extending Neural Architectures to Function Spaces for Operator Learning

A wide range of scientific problems, such as those described by continuous-time dynamical systems and partial differential equations (PDEs), are naturally formulated on function spaces. While function spaces are typically infinite-dimensional, deep learning has predominantly advanced through applications in computer vision and natural language processing that focus on mappings between finite-dimensional spaces. Such fundamental disparities in the nature of the data have limited neural networks from achieving a comparable level of success in scientific applications as seen in other fields. Neural operators are a principled way to generalize neural networks to mappings between function spaces, offering a pathway to replicate deep learning's transformative impact on scientific problems. For instance, neural operators can learn solution operators for entire classes of PDEs, e.g., physical systems with different boundary conditions, coefficient functions, and geometries. A key factor in deep learning's success has been the careful engineering of neural architectures through extensive empirical testing. Translating these neural architectures into neural operators allows operator learning to enjoy these same empirical optimizations. However, prior neural operator architectures have often been introduced as standalone models, not directly derived as extensions of existing neural network architectures. In this paper, we identify and distill the key principles for constructing practical implementations of mappings between infinite-dimensional function spaces. Using these principles, we propose a recipe for converting several popular neural architectures into neural operators with minimal modifications. This paper aims to guide practitioners through this process and details the steps to make neural operators work in practice. Our code can be found at https://github.com/neuraloperator/NNs-to-NOs

Return of ChebNet: Understanding and Improving an Overlooked GNN on Long Range Tasks

ChebNet, one of the earliest spectral GNNs, has largely been overshadowed by Message Passing Neural Networks (MPNNs), which gained popularity for their simplicity and effectiveness in capturing local graph structure. Despite their success, MPNNs are limited in their ability to capture long-range dependencies between nodes. This has led researchers to adapt MPNNs through rewiring or make use of Graph Transformers, which compromises the computational efficiency that characterized early spatial message-passing architectures, and typically disregards the graph structure. Almost a decade after its original introduction, we revisit ChebNet to shed light on its ability to model distant node interactions. We find that out-of-box, ChebNet already shows competitive advantages relative to classical MPNNs and GTs on long-range benchmarks, while maintaining good scalability properties for high-order polynomials. However, we uncover that this polynomial expansion leads ChebNet to an unstable regime during training. To address this limitation, we cast ChebNet as a stable and non-dissipative dynamical system, which we coin Stable-ChebNet. Our Stable-ChebNet model allows for stable information propagation, and has controllable dynamics which do not require the use of eigendecompositions, positional encodings, or graph rewiring. Across several benchmarks, Stable-ChebNet achieves near state-of-the-art performance.

Guided Diffusion Sampling on Function Spaces with Applications to PDEs

We propose a general framework for conditional sampling in PDE-based inverse problems, targeting the recovery of whole solutions from extremely sparse or noisy measurements. This is accomplished by a function-space diffusion model and plug-and-play guidance for conditioning. Our method first trains an unconditional discretization-agnostic denoising model using neural operator architectures. At inference, we refine the samples to satisfy sparse observation data via a gradient-based guidance mechanism. Through rigorous mathematical analysis, we extend Tweedie's formula to infinite-dimensional Hilbert spaces, providing the theoretical foundation for our posterior sampling approach. Our method (FunDPS) accurately captures posterior distributions in function spaces under minimal supervision and severe data scarcity. Across five PDE tasks with only 3% observation, our method achieves an average 32% accuracy improvement over state-of-the-art fixed-resolution diffusion baselines while reducing sampling steps by 4x. Furthermore, multi-resolution fine-tuning ensures strong cross-resolution generalizability. To the best of our knowledge, this is the first diffusion-based framework to operate independently of discretization, offering a practical and flexible solution for forward and inverse problems in the context of PDEs. Code is available at https://github.com/neuraloperator/FunDPS

Deep Physics Prior for First Order Inverse Optimization

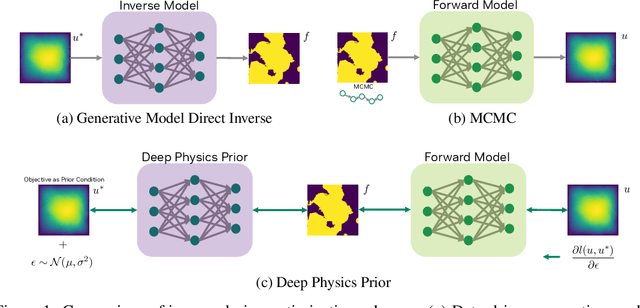
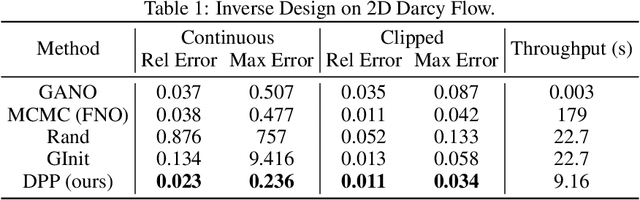
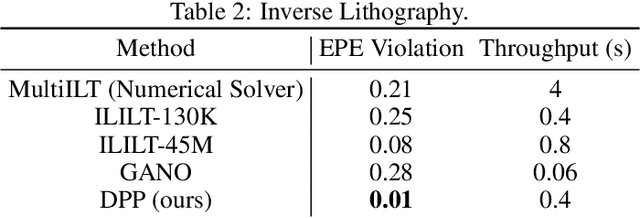
Inverse design optimization aims to infer system parameters from observed solutions, posing critical challenges across domains such as semiconductor manufacturing, structural engineering, materials science, and fluid dynamics. The lack of explicit mathematical representations in many systems complicates this process and makes the first order optimization impossible. Mainstream approaches, including generative AI and Bayesian optimization, address these challenges but have limitations. Generative AI is computationally expensive, while Bayesian optimization, relying on surrogate models, suffers from scalability, sensitivity to priors, and noise issues, often leading to suboptimal solutions. This paper introduces Deep Physics Prior (DPP), a novel method enabling first-order gradient-based inverse optimization with surrogate machine learning models. By leveraging pretrained auxiliary Neural Operators, DPP enforces prior distribution constraints to ensure robust and meaningful solutions. This approach is particularly effective when prior data and observation distributions are unknown.

Enabling Automatic Differentiation with Mollified Graph Neural Operators

Physics-informed neural operators offer a powerful framework for learning solution operators of partial differential equations (PDEs) by combining data and physics losses. However, these physics losses rely on derivatives. Computing these derivatives remains challenging, with spectral and finite difference methods introducing approximation errors due to finite resolution. Here, we propose the mollified graph neural operator (mGNO), the first method to leverage automatic differentiation and compute \emph{exact} gradients on arbitrary geometries. This enhancement enables efficient training on irregular grids and varying geometries while allowing seamless evaluation of physics losses at randomly sampled points for improved generalization. For a PDE example on regular grids, mGNO paired with autograd reduced the L2 relative data error by 20x compared to finite differences, although training was slower. It can also solve PDEs on unstructured point clouds seamlessly, using physics losses only, at resolutions vastly lower than those needed for finite differences to be accurate enough. On these unstructured point clouds, mGNO leads to errors that are consistently 2 orders of magnitude lower than machine learning baselines (Meta-PDE) for comparable runtimes, and also delivers speedups from 1 to 3 orders of magnitude compared to the numerical solver for similar accuracy. mGNOs can also be used to solve inverse design and shape optimization problems on complex geometries.

Ambient Noise Full Waveform Inversion with Neural Operators

Numerical simulations of seismic wave propagation are crucial for investigating velocity structures and improving seismic hazard assessment. However, standard methods such as finite difference or finite element are computationally expensive. Recent studies have shown that a new class of machine learning models, called neural operators, can solve the elastodynamic wave equation orders of magnitude faster than conventional methods. Full waveform inversion is a prime beneficiary of the accelerated simulations. Neural operators, as end-to-end differentiable operators, combined with automatic differentiation, provide an alternative approach to the adjoint-state method. Since neural operators do not involve the Born approximation, when used for full waveform inversion they have the potential to include additional phases and alleviate cycle-skipping problems present in traditional adjoint-state formulations. In this study, we demonstrate the application of neural operators for full waveform inversion on a real seismic dataset, which consists of several nodal transects collected across the San Gabriel, Chino, and San Bernardino basins in the Los Angeles metropolitan area.

Fourier Neural Operator based surrogates for $CO_2$ storage in realistic geologies

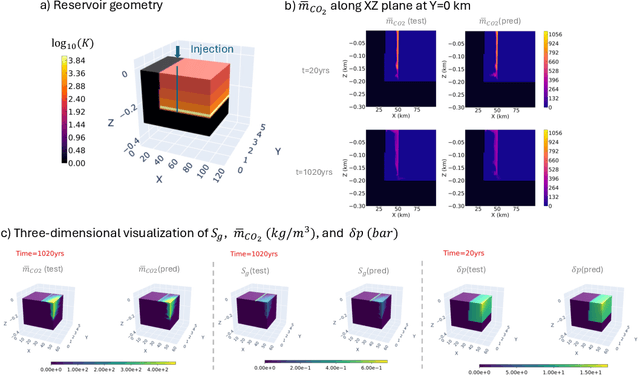
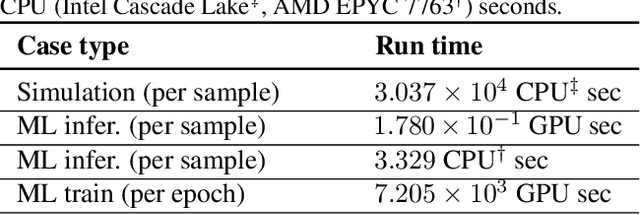
This study aims to develop surrogate models for accelerating decision making processes associated with carbon capture and storage (CCS) technologies. Selection of sub-surface $CO_2$ storage sites often necessitates expensive and involved simulations of $CO_2$ flow fields. Here, we develop a Fourier Neural Operator (FNO) based model for real-time, high-resolution simulation of $CO_2$ plume migration. The model is trained on a comprehensive dataset generated from realistic subsurface parameters and offers $O(10^5)$ computational acceleration with minimal sacrifice in prediction accuracy. We also explore super-resolution experiments to improve the computational cost of training the FNO based models. Additionally, we present various strategies for improving the reliability of predictions from the model, which is crucial while assessing actual geological sites. This novel framework, based on NVIDIA's Modulus library, will allow rapid screening of sites for CCS. The discussed workflows and strategies can be applied to other energy solutions like geothermal reservoir modeling and hydrogen storage. Our work scales scientific machine learning models to realistic 3D systems that are more consistent with real-life subsurface aquifers/reservoirs, paving the way for next-generation digital twins for subsurface CCS applications.

Factorized Implicit Global Convolution for Automotive Computational Fluid Dynamics Prediction

Computational Fluid Dynamics (CFD) is crucial for automotive design, requiring the analysis of large 3D point clouds to study how vehicle geometry affects pressure fields and drag forces. However, existing deep learning approaches for CFD struggle with the computational complexity of processing high-resolution 3D data. We propose Factorized Implicit Global Convolution (FIGConv), a novel architecture that efficiently solves CFD problems for very large 3D meshes with arbitrary input and output geometries. FIGConv achieves quadratic complexity $O(N^2)$, a significant improvement over existing 3D neural CFD models that require cubic complexity $O(N^3)$. Our approach combines Factorized Implicit Grids to approximate high-resolution domains, efficient global convolutions through 2D reparameterization, and a U-shaped architecture for effective information gathering and integration. We validate our approach on the industry-standard Ahmed body dataset and the large-scale DrivAerNet dataset. In DrivAerNet, our model achieves an $R^2$ value of 0.95 for drag prediction, outperforming the previous state-of-the-art by a significant margin. This represents a 40% improvement in relative mean squared error and a 70% improvement in absolute mean squared error over previous methods.

Stochastic Process Learning via Operator Flow Matching

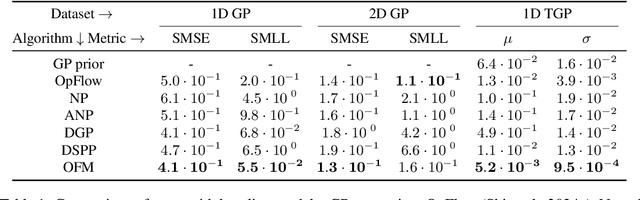
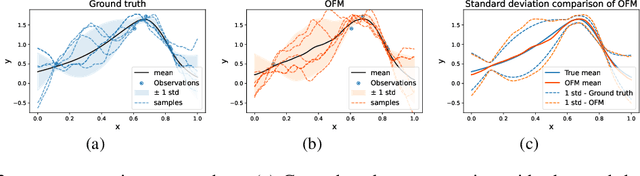
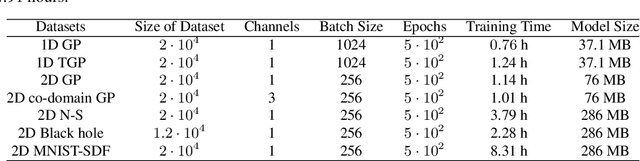
Expanding on neural operators, we propose a novel framework for stochastic process learning across arbitrary domains. In particular, we develop operator flow matching (\alg) for learning stochastic process priors on function spaces. \alg provides the probability density of the values of any collection of points and enables mathematically tractable functional regression at new points with mean and density estimation. Our method outperforms state-of-the-art models in stochastic process learning, functional regression, and prior learning.

Ultrasound Lung Aeration Map via Physics-Aware Neural Operators

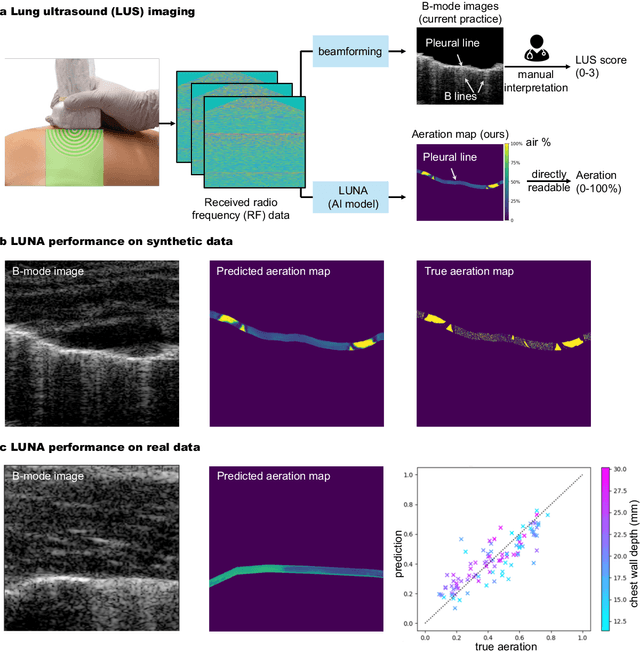
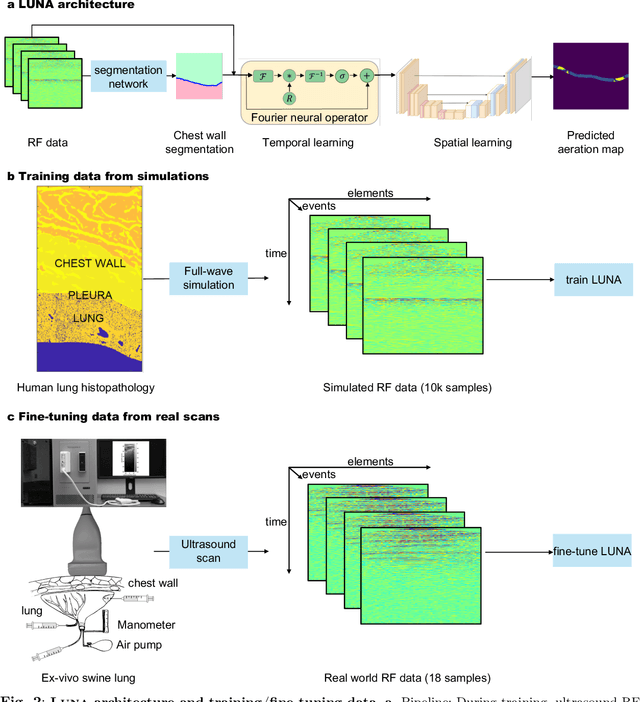
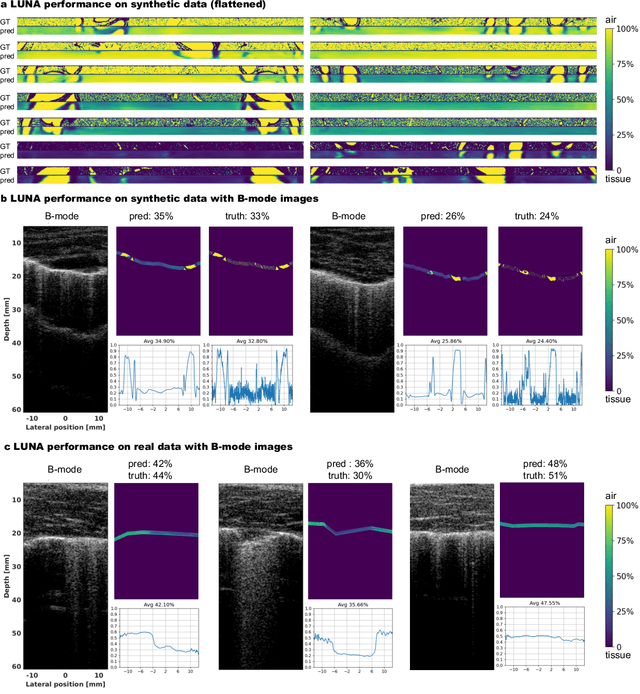
Lung ultrasound is a growing modality in clinics for diagnosing and monitoring acute and chronic lung diseases due to its low cost and accessibility. Lung ultrasound works by emitting diagnostic pulses, receiving pressure waves and converting them into radio frequency (RF) data, which are then processed into B-mode images with beamformers for radiologists to interpret. However, unlike conventional ultrasound for soft tissue anatomical imaging, lung ultrasound interpretation is complicated by complex reverberations from the pleural interface caused by the inability of ultrasound to penetrate air. The indirect B-mode images make interpretation highly dependent on reader expertise, requiring years of training, which limits its widespread use despite its potential for high accuracy in skilled hands. To address these challenges and democratize ultrasound lung imaging as a reliable diagnostic tool, we propose LUNA, an AI model that directly reconstructs lung aeration maps from RF data, bypassing the need for traditional beamformers and indirect interpretation of B-mode images. LUNA uses a Fourier neural operator, which processes RF data efficiently in Fourier space, enabling accurate reconstruction of lung aeration maps. LUNA offers a quantitative, reader-independent alternative to traditional semi-quantitative lung ultrasound scoring methods. The development of LUNA involves synthetic and real data: We simulate synthetic data with an experimentally validated approach and scan ex vivo swine lungs as real data. Trained on abundant simulated data and fine-tuned with a small amount of real-world data, LUNA achieves robust performance, demonstrated by an aeration estimation error of 9% in ex-vivo lung scans. We demonstrate the potential of reconstructing lung aeration maps from RF data, providing a foundation for improving lung ultrasound reproducibility and diagnostic utility.