Enabling Automatic Differentiation with Mollified Graph Neural Operators

Physics-informed neural operators offer a powerful framework for learning solution operators of partial differential equations (PDEs) by combining data and physics losses. However, these physics losses rely on derivatives. Computing these derivatives remains challenging, with spectral and finite difference methods introducing approximation errors due to finite resolution. Here, we propose the mollified graph neural operator (mGNO), the first method to leverage automatic differentiation and compute \emph{exact} gradients on arbitrary geometries. This enhancement enables efficient training on irregular grids and varying geometries while allowing seamless evaluation of physics losses at randomly sampled points for improved generalization. For a PDE example on regular grids, mGNO paired with autograd reduced the L2 relative data error by 20x compared to finite differences, although training was slower. It can also solve PDEs on unstructured point clouds seamlessly, using physics losses only, at resolutions vastly lower than those needed for finite differences to be accurate enough. On these unstructured point clouds, mGNO leads to errors that are consistently 2 orders of magnitude lower than machine learning baselines (Meta-PDE) for comparable runtimes, and also delivers speedups from 1 to 3 orders of magnitude compared to the numerical solver for similar accuracy. mGNOs can also be used to solve inverse design and shape optimization problems on complex geometries.

Pretraining Codomain Attention Neural Operators for Solving Multiphysics PDEs

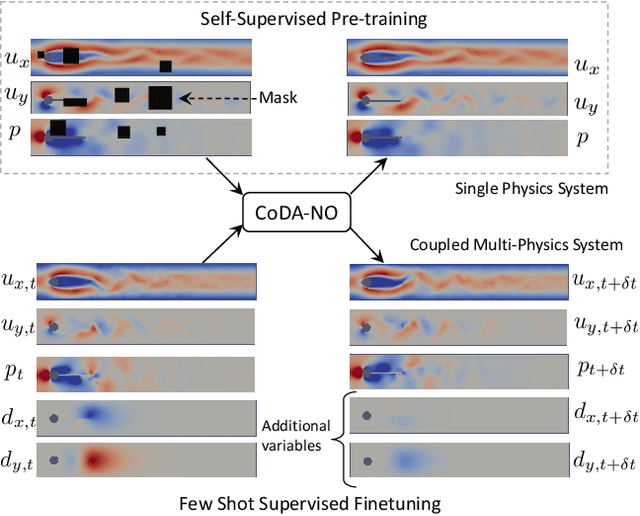
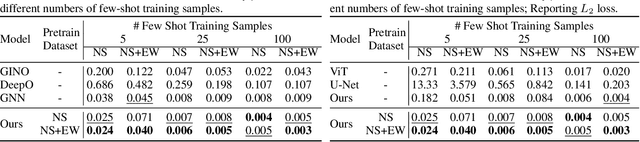
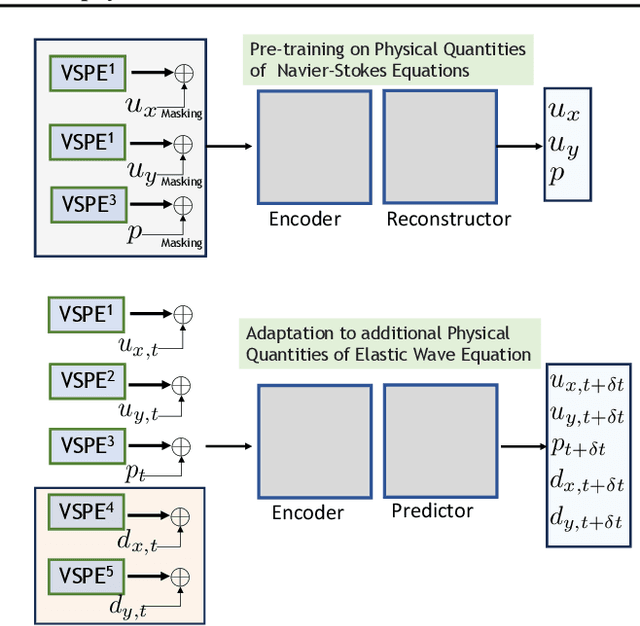
Existing neural operator architectures face challenges when solving multiphysics problems with coupled partial differential equations (PDEs), due to complex geometries, interactions between physical variables, and the lack of large amounts of high-resolution training data. To address these issues, we propose Codomain Attention Neural Operator (CoDA-NO), which tokenizes functions along the codomain or channel space, enabling self-supervised learning or pretraining of multiple PDE systems. Specifically, we extend positional encoding, self-attention, and normalization layers to the function space. CoDA-NO can learn representations of different PDE systems with a single model. We evaluate CoDA-NO's potential as a backbone for learning multiphysics PDEs over multiple systems by considering few-shot learning settings. On complex downstream tasks with limited data, such as fluid flow simulations and fluid-structure interactions, we found CoDA-NO to outperform existing methods on the few-shot learning task by over $36\%$. The code is available at https://github.com/ashiq24/CoDA-NO.

Fourier Continuation for Exact Derivative Computation in Physics-Informed Neural Operators

The physics-informed neural operator (PINO) is a machine learning architecture that has shown promising empirical results for learning partial differential equations. PINO uses the Fourier neural operator (FNO) architecture to overcome the optimization challenges often faced by physics-informed neural networks. Since the convolution operator in PINO uses the Fourier series representation, its gradient can be computed exactly on the Fourier space. While Fourier series cannot represent nonperiodic functions, PINO and FNO still have the expressivity to learn nonperiodic problems with Fourier extension via padding. However, computing the Fourier extension in the physics-informed optimization requires solving an ill-conditioned system, resulting in inaccurate derivatives which prevent effective optimization. In this work, we present an architecture that leverages Fourier continuation (FC) to apply the exact gradient method to PINO for nonperiodic problems. This paper investigates three different ways that FC can be incorporated into PINO by testing their performance on a 1D blowup problem. Experiments show that FC-PINO outperforms padded PINO, improving equation loss by several orders of magnitude, and it can accurately capture the third order derivatives of nonsmooth solution functions.