TorchLean: Formalizing Neural Networks in Lean

Neural networks are increasingly deployed in safety- and mission-critical pipelines, yet many verification and analysis results are produced outside the programming environment that defines and runs the model. This separation creates a semantic gap between the executed network and the analyzed artifact, so guarantees can hinge on implicit conventions such as operator semantics, tensor layouts, preprocessing, and floating-point corner cases. We introduce TorchLean, a framework in the Lean 4 theorem prover that treats learned models as first-class mathematical objects with a single, precise semantics shared by execution and verification. TorchLean unifies (1) a PyTorch-style verified API with eager and compiled modes that lower to a shared op-tagged SSA/DAG computation-graph IR, (2) explicit Float32 semantics via an executable IEEE-754 binary32 kernel and proof-relevant rounding models, and (3) verification via IBP and CROWN/LiRPA-style bound propagation with certificate checking. We validate TorchLean end-to-end on certified robustness, physics-informed residual bounds for PINNs, and Lyapunov-style neural controller verification, alongside mechanized theoretical results including a universal approximation theorem. These results demonstrate a semantics-first infrastructure for fully formal, end-to-end verification of learning-enabled systems.

QEDBENCH: Quantifying the Alignment Gap in Automated Evaluation of University-Level Mathematical Proofs

As Large Language Models (LLMs) saturate elementary benchmarks, the research frontier has shifted from generation to the reliability of automated evaluation. We demonstrate that standard "LLM-as-a-Judge" protocols suffer from a systematic Alignment Gap when applied to upper-undergraduate to early graduate level mathematics. To quantify this, we introduce QEDBench, the first large-scale dual-rubric alignment benchmark to systematically measure alignment with human experts on university-level math proofs by contrasting course-specific rubrics against expert common knowledge criteria. By deploying a dual-evaluation matrix (7 judges x 5 solvers) against 1,000+ hours of human evaluation, we reveal that certain frontier evaluators like Claude Opus 4.5, DeepSeek-V3, Qwen 2.5 Max, and Llama 4 Maverick exhibit significant positive bias (up to +0.18, +0.20, +0.30, +0.36 mean score inflation, respectively). Furthermore, we uncover a critical reasoning gap in the discrete domain: while Gemini 3.0 Pro achieves state-of-the-art performance (0.91 average human evaluation score), other reasoning models like GPT-5 Pro and Claude Sonnet 4.5 see their performance significantly degrade in discrete domains. Specifically, their average human evaluation scores drop to 0.72 and 0.63 in Discrete Math, and to 0.74 and 0.50 in Graph Theory. In addition to these research results, we also release QEDBench as a public benchmark for evaluating and improving AI judges. Our benchmark is publicly published at https://github.com/qqliu/Yale-QEDBench.

LeanProgress: Guiding Search for Neural Theorem Proving via Proof Progress Prediction

Mathematical reasoning remains a significant challenge for Large Language Models (LLMs) due to hallucinations. When combined with formal proof assistants like Lean, these hallucinations can be eliminated through rigorous verification, making theorem proving reliable. However, even with formal verification, LLMs still struggle with long proofs and complex mathematical formalizations. While Lean with LLMs offers valuable assistance with retrieving lemmas, generating tactics, or even complete proofs, it lacks a crucial capability: providing a sense of proof progress. This limitation particularly impacts the overall development efficiency in large formalization projects. We introduce LeanProgress, a method that predicts the progress in the proof. Training and evaluating our models made on a large corpus of Lean proofs from Lean Workbook Plus and Mathlib4 and how many steps remain to complete it, we employ data preprocessing and balancing techniques to handle the skewed distribution of proof lengths. Our experiments show that LeanProgress achieves an overall prediction accuracy of 75.1\% in predicting the amount of progress and, hence, the remaining number of steps. When integrated into a best-first search framework using Reprover, our method shows a 3.8\% improvement on Mathlib4 compared to baseline performances of 41.2\%, particularly for longer proofs. These results demonstrate how proof progress prediction can enhance both automated and interactive theorem proving, enabling users to make more informed decisions about proof strategies.

Tensor-GaLore: Memory-Efficient Training via Gradient Tensor Decomposition

We present Tensor-GaLore, a novel method for efficient training of neural networks with higher-order tensor weights. Many models, particularly those used in scientific computing, employ tensor-parameterized layers to capture complex, multidimensional relationships. When scaling these methods to high-resolution problems makes memory usage grow intractably, and matrix based optimization methods lead to suboptimal performance and compression. We propose to work directly in the high-order space of the complex tensor parameter space using a tensor factorization of the gradients during optimization. We showcase its effectiveness on Fourier Neural Operators (FNOs), a class of models crucial for solving partial differential equations (PDE) and prove the theory of it. Across various PDE tasks like the Navier Stokes and Darcy Flow equations, Tensor-GaLore achieves substantial memory savings, reducing optimizer memory usage by up to 75%. These substantial memory savings across AI for science demonstrate Tensor-GaLore's potential.

A Library for Learning Neural Operators

We present NeuralOperator, an open-source Python library for operator learning. Neural operators generalize neural networks to maps between function spaces instead of finite-dimensional Euclidean spaces. They can be trained and inferenced on input and output functions given at various discretizations, satisfying a discretization convergence properties. Built on top of PyTorch, NeuralOperator provides all the tools for training and deploying neural operator models, as well as developing new ones, in a high-quality, tested, open-source package. It combines cutting-edge models and customizability with a gentle learning curve and simple user interface for newcomers.

LeanAgent: Lifelong Learning for Formal Theorem Proving

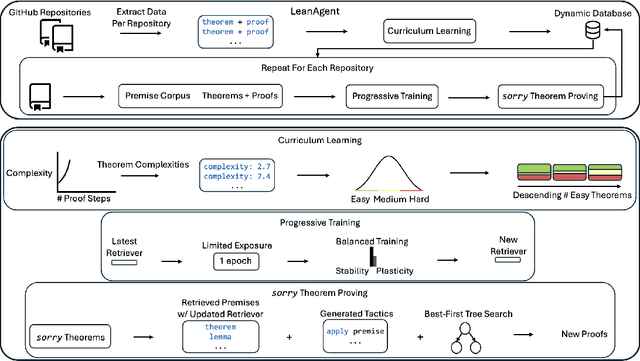
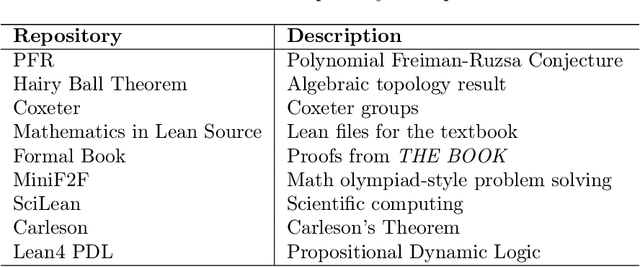
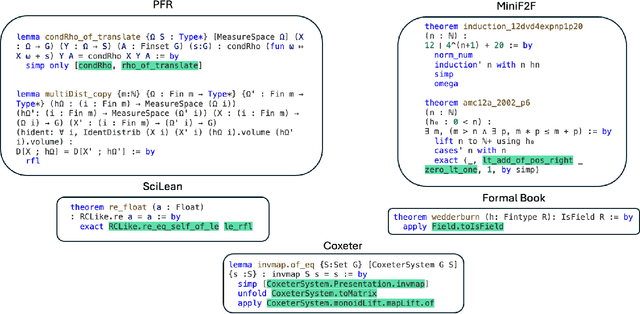
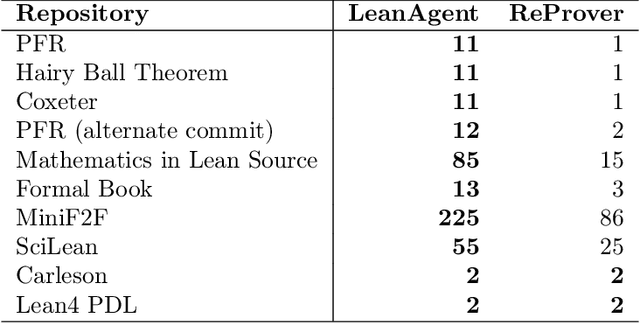
Large Language Models (LLMs) have been successful in mathematical reasoning tasks such as formal theorem proving when integrated with interactive proof assistants like Lean. Existing approaches involve training or fine-tuning an LLM on a specific dataset to perform well on particular domains, such as undergraduate-level mathematics. These methods struggle with generalizability to advanced mathematics. A fundamental limitation is that these approaches operate on static domains, failing to capture how mathematicians often work across multiple domains and projects simultaneously or cyclically. We present LeanAgent, a novel lifelong learning framework for theorem proving that continuously generalizes to and improves on ever-expanding mathematical knowledge without forgetting previously learned knowledge. LeanAgent introduces several key innovations, including a curriculum learning strategy that optimizes the learning trajectory in terms of mathematical difficulty, a dynamic database for efficient management of evolving mathematical knowledge, and progressive training to balance stability and plasticity. LeanAgent successfully proves 162 theorems previously unproved by humans across 23 diverse Lean repositories, many from advanced mathematics. It performs up to 11$\times$ better than the static LLM baseline, proving challenging theorems in domains like abstract algebra and algebraic topology while showcasing a clear progression of learning from basic concepts to advanced topics. In addition, we analyze LeanAgent's superior performance on key lifelong learning metrics. LeanAgent achieves exceptional scores in stability and backward transfer, where learning new tasks improves performance on previously learned tasks. This emphasizes LeanAgent's continuous generalizability and improvement, explaining its superior theorem proving performance.

Pretraining Codomain Attention Neural Operators for Solving Multiphysics PDEs

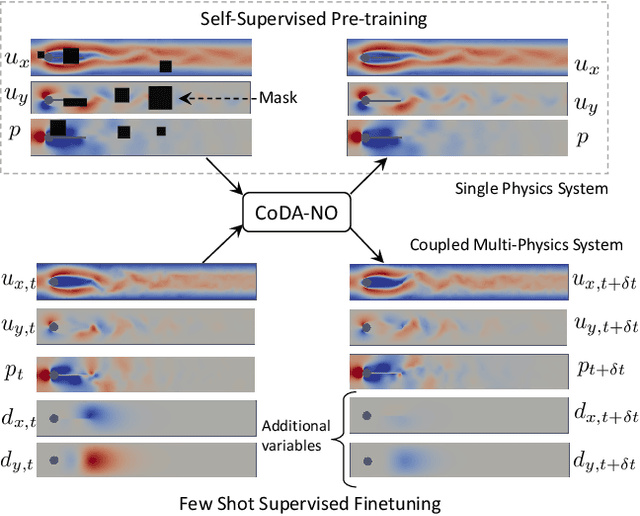
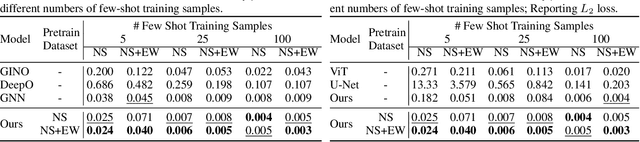
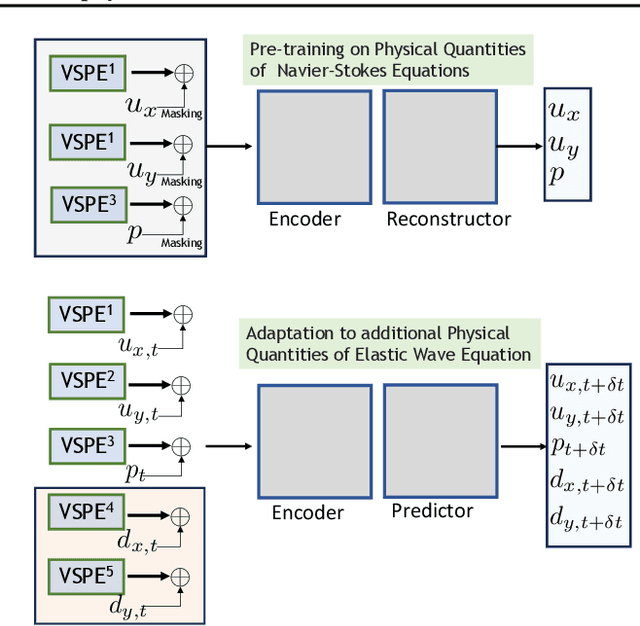
Existing neural operator architectures face challenges when solving multiphysics problems with coupled partial differential equations (PDEs), due to complex geometries, interactions between physical variables, and the lack of large amounts of high-resolution training data. To address these issues, we propose Codomain Attention Neural Operator (CoDA-NO), which tokenizes functions along the codomain or channel space, enabling self-supervised learning or pretraining of multiple PDE systems. Specifically, we extend positional encoding, self-attention, and normalization layers to the function space. CoDA-NO can learn representations of different PDE systems with a single model. We evaluate CoDA-NO's potential as a backbone for learning multiphysics PDEs over multiple systems by considering few-shot learning settings. On complex downstream tasks with limited data, such as fluid flow simulations and fluid-structure interactions, we found CoDA-NO to outperform existing methods on the few-shot learning task by over $36\%$. The code is available at https://github.com/ashiq24/CoDA-NO.

Incremental Fourier Neural Operator

Recently, neural networks have proven their impressive ability to solve partial differential equations (PDEs). Among them, Fourier neural operator (FNO) has shown success in learning solution operators for highly non-linear problems such as turbulence flow. FNO is discretization-invariant, where it can be trained on low-resolution data and generalizes to problems with high-resolution. This property is related to the low-pass filters in FNO, where only a limited number of frequency modes are selected to propagate information. However, it is still a challenge to select an appropriate number of frequency modes and training resolution for different PDEs. Too few frequency modes and low-resolution data hurt generalization, while too many frequency modes and high-resolution data are computationally expensive and lead to over-fitting. To this end, we propose Incremental Fourier Neural Operator (IFNO), which augments both the frequency modes and data resolution incrementally during training. We show that IFNO achieves better generalization (around 15% reduction on testing L2 loss) while reducing the computational cost by 35%, compared to the standard FNO. In addition, we observe that IFNO follows the behavior of implicit regularization in FNO, which explains its excellent generalization ability.