Youtu-Agent: Scaling Agent Productivity with Automated Generation and Hybrid Policy Optimization

Existing Large Language Model (LLM) agent frameworks face two significant challenges: high configuration costs and static capabilities. Building a high-quality agent often requires extensive manual effort in tool integration and prompt engineering, while deployed agents struggle to adapt to dynamic environments without expensive fine-tuning. To address these issues, we propose \textbf{Youtu-Agent}, a modular framework designed for the automated generation and continuous evolution of LLM agents. Youtu-Agent features a structured configuration system that decouples execution environments, toolkits, and context management, enabling flexible reuse and automated synthesis. We introduce two generation paradigms: a \textbf{Workflow} mode for standard tasks and a \textbf{Meta-Agent} mode for complex, non-standard requirements, capable of automatically generating tool code, prompts, and configurations. Furthermore, Youtu-Agent establishes a hybrid policy optimization system: (1) an \textbf{Agent Practice} module that enables agents to accumulate experience and improve performance through in-context optimization without parameter updates; and (2) an \textbf{Agent RL} module that integrates with distributed training frameworks to enable scalable and stable reinforcement learning of any Youtu-Agents in an end-to-end, large-scale manner. Experiments demonstrate that Youtu-Agent achieves state-of-the-art performance on WebWalkerQA (71.47\%) and GAIA (72.8\%) using open-weight models. Our automated generation pipeline achieves over 81\% tool synthesis success rate, while the Practice module improves performance on AIME 2024/2025 by +2.7\% and +5.4\% respectively. Moreover, our Agent RL training achieves 40\% speedup with steady performance improvement on 7B LLMs, enhancing coding/reasoning and searching capabilities respectively up to 35\% and 21\% on Maths and general/multi-hop QA benchmarks.

Youtu-LLM: Unlocking the Native Agentic Potential for Lightweight Large Language Models

We introduce Youtu-LLM, a lightweight yet powerful language model that harmonizes high computational efficiency with native agentic intelligence. Unlike typical small models that rely on distillation, Youtu-LLM (1.96B) is pre-trained from scratch to systematically cultivate reasoning and planning capabilities. The key technical advancements are as follows: (1) Compact Architecture with Long-Context Support: Built on a dense Multi-Latent Attention (MLA) architecture with a novel STEM-oriented vocabulary, Youtu-LLM supports a 128k context window. This design enables robust long-context reasoning and state tracking within a minimal memory footprint, making it ideal for long-horizon agent and reasoning tasks. (2) Principled "Commonsense-STEM-Agent" Curriculum: We curated a massive corpus of approximately 11T tokens and implemented a multi-stage training strategy. By progressively shifting the pre-training data distribution from general commonsense to complex STEM and agentic tasks, we ensure the model acquires deep cognitive abilities rather than superficial alignment. (3) Scalable Agentic Mid-training: Specifically for the agentic mid-training, we employ diverse data construction schemes to synthesize rich and varied trajectories across math, coding, and tool-use domains. This high-quality data enables the model to internalize planning and reflection behaviors effectively. Extensive evaluations show that Youtu-LLM sets a new state-of-the-art for sub-2B LLMs. On general benchmarks, it achieves competitive performance against larger models, while on agent-specific tasks, it significantly surpasses existing SOTA baselines, demonstrating that lightweight models can possess strong intrinsic agentic capabilities.

SmartSnap: Proactive Evidence Seeking for Self-Verifying Agents

Agentic reinforcement learning (RL) holds great promise for the development of autonomous agents under complex GUI tasks, but its scalability remains severely hampered by the verification of task completion. Existing task verification is treated as a passive, post-hoc process: a verifier (i.e., rule-based scoring script, reward or critic model, and LLM-as-a-Judge) analyzes the agent's entire interaction trajectory to determine if the agent succeeds. Such processing of verbose context that contains irrelevant, noisy history poses challenges to the verification protocols and therefore leads to prohibitive cost and low reliability. To overcome this bottleneck, we propose SmartSnap, a paradigm shift from this passive, post-hoc verification to proactive, in-situ self-verification by the agent itself. We introduce the Self-Verifying Agent, a new type of agent designed with dual missions: to not only complete a task but also to prove its accomplishment with curated snapshot evidences. Guided by our proposed 3C Principles (Completeness, Conciseness, and Creativity), the agent leverages its accessibility to the online environment to perform self-verification on a minimal, decisive set of snapshots. Such evidences are provided as the sole materials for a general LLM-as-a-Judge verifier to determine their validity and relevance. Experiments on mobile tasks across model families and scales demonstrate that our SmartSnap paradigm allows training LLM-driven agents in a scalable manner, bringing performance gains up to 26.08% and 16.66% respectively to 8B and 30B models. The synergizing between solution finding and evidence seeking facilitates the cultivation of efficient, self-verifying agents with competitive performance against DeepSeek V3.1 and Qwen3-235B-A22B.

Counterfactual LLM-based Framework for Measuring Rhetorical Style

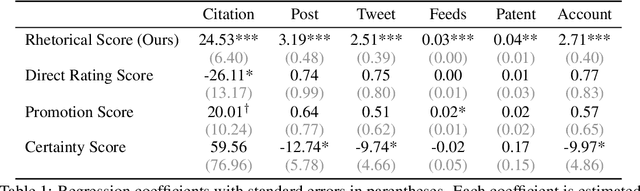
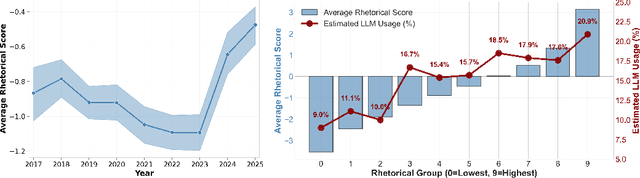
The rise of AI has fueled growing concerns about ``hype'' in machine learning papers, yet a reliable way to quantify rhetorical style independently of substantive content has remained elusive. Because bold language can stem from either strong empirical results or mere rhetorical style, it is often difficult to distinguish between the two. To disentangle rhetorical style from substantive content, we introduce a counterfactual, LLM-based framework: multiple LLM rhetorical personas generate counterfactual writings from the same substantive content, an LLM judge compares them through pairwise evaluations, and the outcomes are aggregated using a Bradley--Terry model. Applying this method to 8,485 ICLR submissions sampled from 2017 to 2025, we generate more than 250,000 counterfactual writings and provide a large-scale quantification of rhetorical style in ML papers. We find that visionary framing significantly predicts downstream attention, including citations and media attention, even after controlling for peer-review evaluations. We also observe a sharp rise in rhetorical strength after 2023, and provide empirical evidence showing that this increase is largely driven by the adoption of LLM-based writing assistance. The reliability of our framework is validated by its robustness to the choice of personas and the high correlation between LLM judgments and human annotations. Our work demonstrates that LLMs can serve as instruments to measure and improve scientific evaluation.

Learn the Ropes, Then Trust the Wins: Self-imitation with Progressive Exploration for Agentic Reinforcement Learning

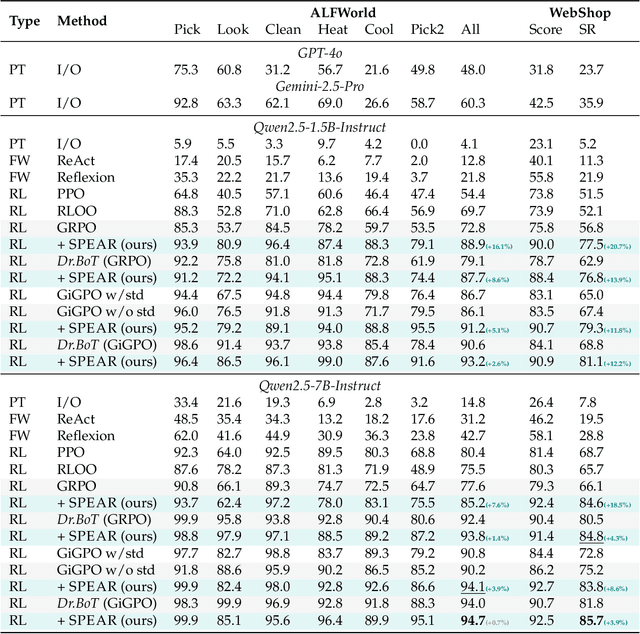
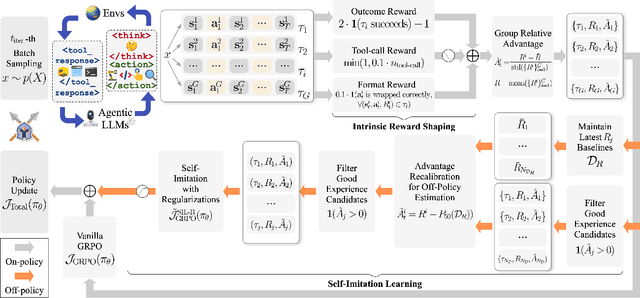
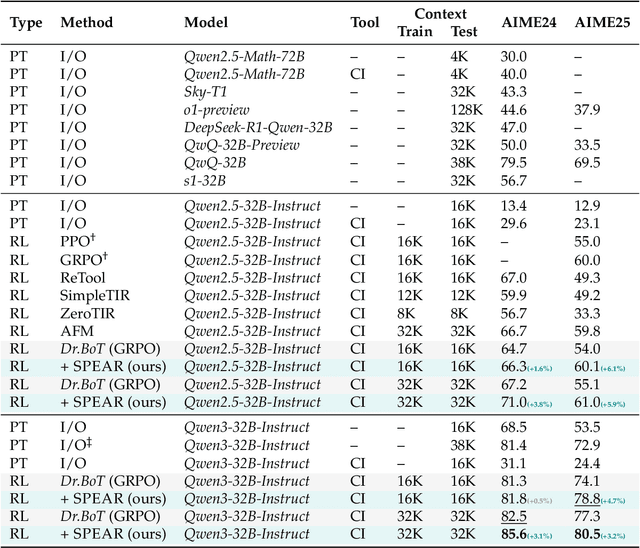
Reinforcement learning (RL) is the dominant paradigm for sharpening strategic tool use capabilities of LLMs on long-horizon, sparsely-rewarded agent tasks, yet it faces a fundamental challenge of exploration-exploitation trade-off. Existing studies stimulate exploration through the lens of policy entropy, but such mechanical entropy maximization is prone to RL training instability due to the multi-turn distribution shifting. In this paper, we target the progressive exploration-exploitation balance under the guidance of the agent own experiences without succumbing to either entropy collapsing or runaway divergence. We propose SPEAR, a curriculum-based self-imitation learning (SIL) recipe for training agentic LLMs. It extends the vanilla SIL framework, where a replay buffer stores self-generated promising trajectories for off-policy update, by gradually steering the policy evolution within a well-balanced range of entropy across stages. Specifically, our approach incorporates a curriculum to manage the exploration process, utilizing intrinsic rewards to foster skill-level exploration and facilitating action-level exploration through SIL. At first, the auxiliary tool call reward plays a critical role in the accumulation of tool-use skills, enabling broad exposure to the unfamiliar distributions of the environment feedback with an upward entropy trend. As training progresses, self-imitation gets strengthened to exploit existing successful patterns from replayed experiences for comparative action-level exploration, accelerating solution iteration without unbounded entropy growth. To further stabilize training, we recalibrate the advantages of experiences in the replay buffer to address the potential policy drift. Reugularizations such as the clipping of tokens with high covariance between probability and advantage are introduced to the trajectory-level entropy control to curb over-confidence.

Geometric Operator Learning with Optimal Transport

We propose integrating optimal transport (OT) into operator learning for partial differential equations (PDEs) on complex geometries. Classical geometric learning methods typically represent domains as meshes, graphs, or point clouds. Our approach generalizes discretized meshes to mesh density functions, formulating geometry embedding as an OT problem that maps these functions to a uniform density in a reference space. Compared to previous methods relying on interpolation or shared deformation, our OT-based method employs instance-dependent deformation, offering enhanced flexibility and effectiveness. For 3D simulations focused on surfaces, our OT-based neural operator embeds the surface geometry into a 2D parameterized latent space. By performing computations directly on this 2D representation of the surface manifold, it achieves significant computational efficiency gains compared to volumetric simulation. Experiments with Reynolds-averaged Navier-Stokes equations (RANS) on the ShapeNet-Car and DrivAerNet-Car datasets show that our method achieves better accuracy and also reduces computational expenses in terms of both time and memory usage compared to existing machine learning models. Additionally, our model demonstrates significantly improved accuracy on the FlowBench dataset, underscoring the benefits of employing instance-dependent deformation for datasets with highly variable geometries.

High precision PINNs in unbounded domains: application to singularity formulation in PDEs

We investigate the high-precision training of Physics-Informed Neural Networks (PINNs) in unbounded domains, with a special focus on applications to singularity formulation in PDEs. We propose a modularized approach and study the choices of neural network ansatz, sampling strategy, and optimization algorithm. When combined with rigorous computer-assisted proofs and PDE analysis, the numerical solutions identified by PINNs, provided they are of high precision, can serve as a powerful tool for studying singularities in PDEs. For 1D Burgers equation, our framework can lead to a solution with very high precision, and for the 2D Boussinesq equation, which is directly related to the singularity formulation in 3D Euler and Navier-Stokes equations, we obtain a solution whose loss is $4$ digits smaller than that obtained in \cite{wang2023asymptotic} with fewer training steps. We also discuss potential directions for pushing towards machine precision for higher-dimensional problems.

Ultrasound Lung Aeration Map via Physics-Aware Neural Operators

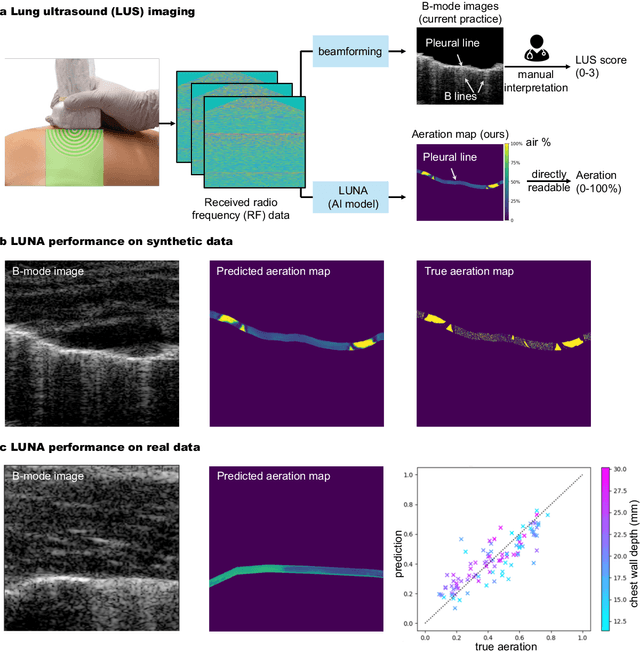
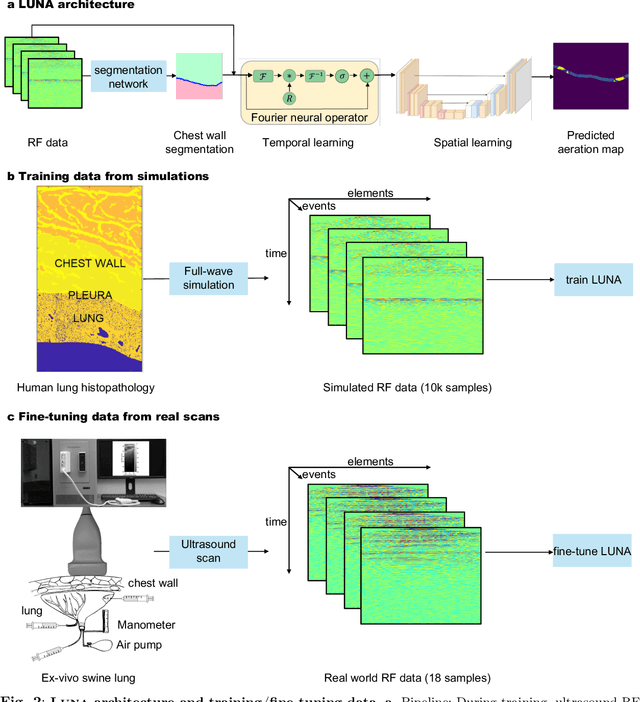
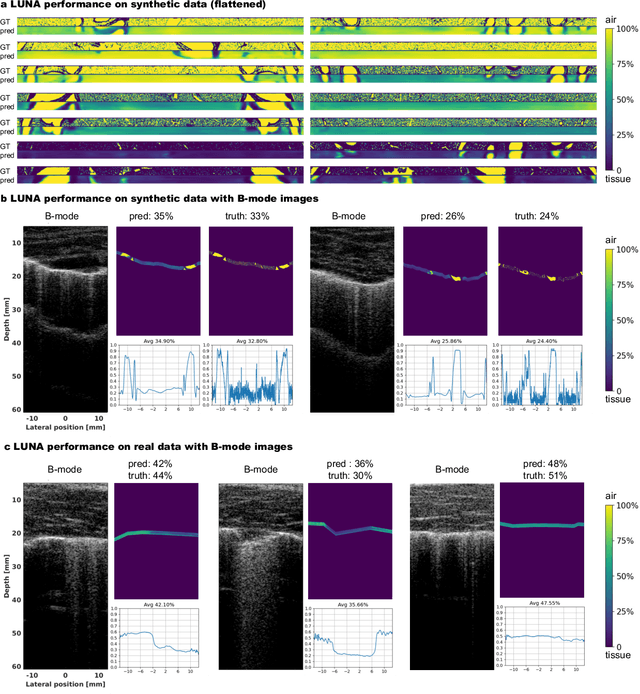
Lung ultrasound is a growing modality in clinics for diagnosing and monitoring acute and chronic lung diseases due to its low cost and accessibility. Lung ultrasound works by emitting diagnostic pulses, receiving pressure waves and converting them into radio frequency (RF) data, which are then processed into B-mode images with beamformers for radiologists to interpret. However, unlike conventional ultrasound for soft tissue anatomical imaging, lung ultrasound interpretation is complicated by complex reverberations from the pleural interface caused by the inability of ultrasound to penetrate air. The indirect B-mode images make interpretation highly dependent on reader expertise, requiring years of training, which limits its widespread use despite its potential for high accuracy in skilled hands. To address these challenges and democratize ultrasound lung imaging as a reliable diagnostic tool, we propose LUNA, an AI model that directly reconstructs lung aeration maps from RF data, bypassing the need for traditional beamformers and indirect interpretation of B-mode images. LUNA uses a Fourier neural operator, which processes RF data efficiently in Fourier space, enabling accurate reconstruction of lung aeration maps. LUNA offers a quantitative, reader-independent alternative to traditional semi-quantitative lung ultrasound scoring methods. The development of LUNA involves synthetic and real data: We simulate synthetic data with an experimentally validated approach and scan ex vivo swine lungs as real data. Trained on abundant simulated data and fine-tuned with a small amount of real-world data, LUNA achieves robust performance, demonstrated by an aeration estimation error of 9% in ex-vivo lung scans. We demonstrate the potential of reconstructing lung aeration maps from RF data, providing a foundation for improving lung ultrasound reproducibility and diagnostic utility.

A Library for Learning Neural Operators

We present NeuralOperator, an open-source Python library for operator learning. Neural operators generalize neural networks to maps between function spaces instead of finite-dimensional Euclidean spaces. They can be trained and inferenced on input and output functions given at various discretizations, satisfying a discretization convergence properties. Built on top of PyTorch, NeuralOperator provides all the tools for training and deploying neural operator models, as well as developing new ones, in a high-quality, tested, open-source package. It combines cutting-edge models and customizability with a gentle learning curve and simple user interface for newcomers.

ARLON: Boosting Diffusion Transformers with Autoregressive Models for Long Video Generation

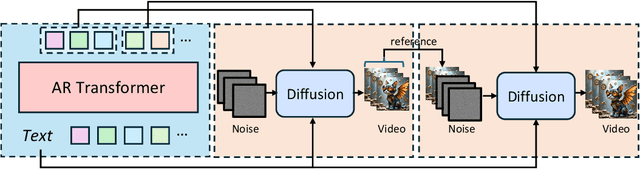
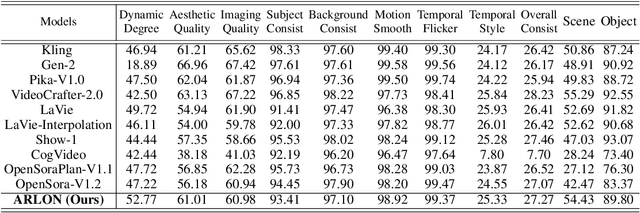
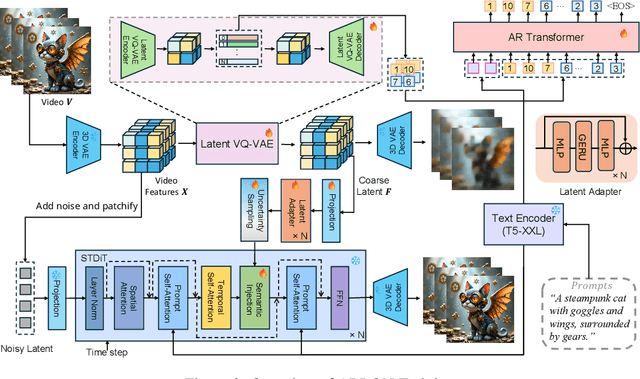
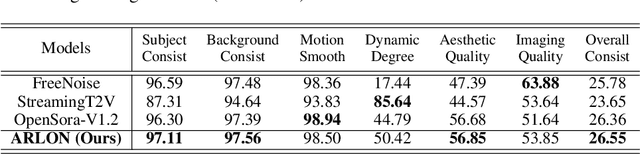
Text-to-video models have recently undergone rapid and substantial advancements. Nevertheless, due to limitations in data and computational resources, achieving efficient generation of long videos with rich motion dynamics remains a significant challenge. To generate high-quality, dynamic, and temporally consistent long videos, this paper presents ARLON, a novel framework that boosts diffusion Transformers with autoregressive models for long video generation, by integrating the coarse spatial and long-range temporal information provided by the AR model to guide the DiT model. Specifically, ARLON incorporates several key innovations: 1) A latent Vector Quantized Variational Autoencoder (VQ-VAE) compresses the input latent space of the DiT model into compact visual tokens, bridging the AR and DiT models and balancing the learning complexity and information density; 2) An adaptive norm-based semantic injection module integrates the coarse discrete visual units from the AR model into the DiT model, ensuring effective guidance during video generation; 3) To enhance the tolerance capability of noise introduced from the AR inference, the DiT model is trained with coarser visual latent tokens incorporated with an uncertainty sampling module. Experimental results demonstrate that ARLON significantly outperforms the baseline OpenSora-V1.2 on eight out of eleven metrics selected from VBench, with notable improvements in dynamic degree and aesthetic quality, while delivering competitive results on the remaining three and simultaneously accelerating the generation process. In addition, ARLON achieves state-of-the-art performance in long video generation. Detailed analyses of the improvements in inference efficiency are presented, alongside a practical application that demonstrates the generation of long videos using progressive text prompts. See demos of ARLON at \url{http://aka.ms/arlon}.