Md Ashiqur Rahman
CLIPSym: Delving into Symmetry Detection with CLIP
Aug 19, 2025Abstract:Symmetry is one of the most fundamental geometric cues in computer vision, and detecting it has been an ongoing challenge. With the recent advances in vision-language models,~i.e., CLIP, we investigate whether a pre-trained CLIP model can aid symmetry detection by leveraging the additional symmetry cues found in the natural image descriptions. We propose CLIPSym, which leverages CLIP's image and language encoders and a rotation-equivariant decoder based on a hybrid of Transformer and $G$-Convolution to detect rotation and reflection symmetries. To fully utilize CLIP's language encoder, we have developed a novel prompting technique called Semantic-Aware Prompt Grouping (SAPG), which aggregates a diverse set of frequent object-based prompts to better integrate the semantic cues for symmetry detection. Empirically, we show that CLIPSym outperforms the current state-of-the-art on three standard symmetry detection datasets (DENDI, SDRW, and LDRS). Finally, we conduct detailed ablations verifying the benefits of CLIP's pre-training, the proposed equivariant decoder, and the SAPG technique. The code is available at https://github.com/timyoung2333/CLIPSym.
Local Scale Equivariance with Latent Deep Equilibrium Canonicalizer
Aug 19, 2025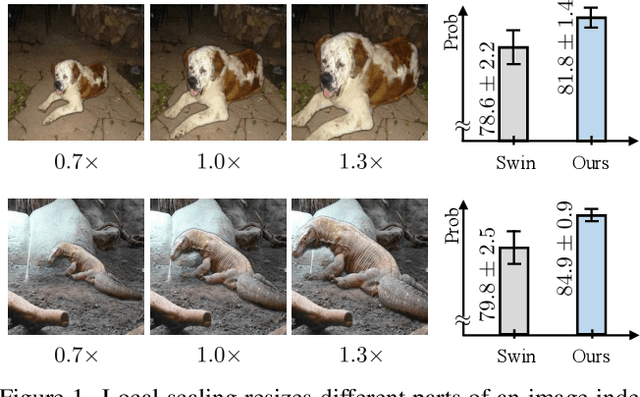
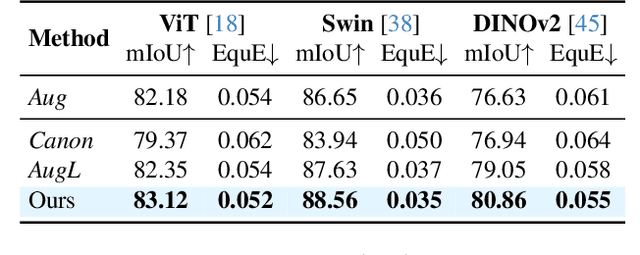
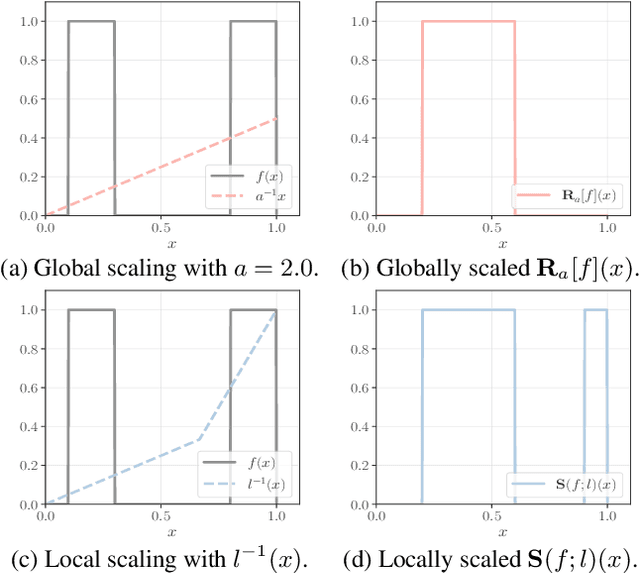

Abstract:Scale variation is a fundamental challenge in computer vision. Objects of the same class can have different sizes, and their perceived size is further affected by the distance from the camera. These variations are local to the objects, i.e., different object sizes may change differently within the same image. To effectively handle scale variations, we present a deep equilibrium canonicalizer (DEC) to improve the local scale equivariance of a model. DEC can be easily incorporated into existing network architectures and can be adapted to a pre-trained model. Notably, we show that on the competitive ImageNet benchmark, DEC improves both model performance and local scale consistency across four popular pre-trained deep-nets, e.g., ViT, DeiT, Swin, and BEiT. Our code is available at https://github.com/ashiq24/local-scale-equivariance.
Group Downsampling with Equivariant Anti-aliasing
Apr 24, 2025Abstract:Downsampling layers are crucial building blocks in CNN architectures, which help to increase the receptive field for learning high-level features and reduce the amount of memory/computation in the model. In this work, we study the generalization of the uniform downsampling layer for group equivariant architectures, e.g., G-CNNs. That is, we aim to downsample signals (feature maps) on general finite groups with anti-aliasing. This involves the following: (a) Given a finite group and a downsampling rate, we present an algorithm to form a suitable choice of subgroup. (b) Given a group and a subgroup, we study the notion of bandlimited-ness and propose how to perform anti-aliasing. Notably, our method generalizes the notion of downsampling based on classical sampling theory. When the signal is on a cyclic group, i.e., periodic, our method recovers the standard downsampling of an ideal low-pass filter followed by a subsampling operation. Finally, we conducted experiments on image classification tasks demonstrating that the proposed downsampling operation improves accuracy, better preserves equivariance, and reduces model size when incorporated into G-equivariant networks
HessianForge: Scalable LiDAR reconstruction with Physics-Informed Neural Representation and Smoothness Energy Constraints
Mar 11, 2025Abstract:Accurate and efficient 3D mapping of large-scale outdoor environments from LiDAR measurements is a fundamental challenge in robotics, particularly towards ensuring smooth and artifact-free surface reconstructions. Although the state-of-the-art methods focus on memory-efficient neural representations for high-fidelity surface generation, they often fail to produce artifact-free manifolds, with artifacts arising due to noisy and sparse inputs. To address this issue, we frame surface mapping as a physics-informed energy optimization problem, enforcing surface smoothness by optimizing an energy functional that penalizes sharp surface ridges. Specifically, we propose a deep learning based approach that learns the signed distance field (SDF) of the surface manifold from raw LiDAR point clouds using a physics-informed loss function that optimizes the $L_2$-Hessian energy of the surface. Our learning framework includes a hierarchical octree based input feature encoding and a multi-scale neural network to iteratively refine the signed distance field at different scales of resolution. Lastly, we introduce a test-time refinement strategy to correct topological inconsistencies and edge distortions that can arise in the generated mesh. We propose a \texttt{CUDA}-accelerated least-squares optimization that locally adjusts vertex positions to enforce feature-preserving smoothing. We evaluate our approach on large-scale outdoor datasets and demonstrate that our approach outperforms current state-of-the-art methods in terms of improved accuracy and smoothness. Our code is available at \href{https://github.com/HrishikeshVish/HessianForge/}{https://github.com/HrishikeshVish/HessianForge/}
MosquitoFusion: A Multiclass Dataset for Real-Time Detection of Mosquitoes, Swarms, and Breeding Sites Using Deep Learning
Apr 01, 2024Abstract:In this paper, we present an integrated approach to real-time mosquito detection using our multiclass dataset (MosquitoFusion) containing 1204 diverse images and leverage cutting-edge technologies, specifically computer vision, to automate the identification of Mosquitoes, Swarms, and Breeding Sites. The pre-trained YOLOv8 model, trained on this dataset, achieved a mean Average Precision (mAP@50) of 57.1%, with precision at 73.4% and recall at 50.5%. The integration of Geographic Information Systems (GIS) further enriches the depth of our analysis, providing valuable insights into spatial patterns. The dataset and code are available at https://github.com/faiyazabdullah/MosquitoFusion.
Pretraining Codomain Attention Neural Operators for Solving Multiphysics PDEs
Mar 19, 2024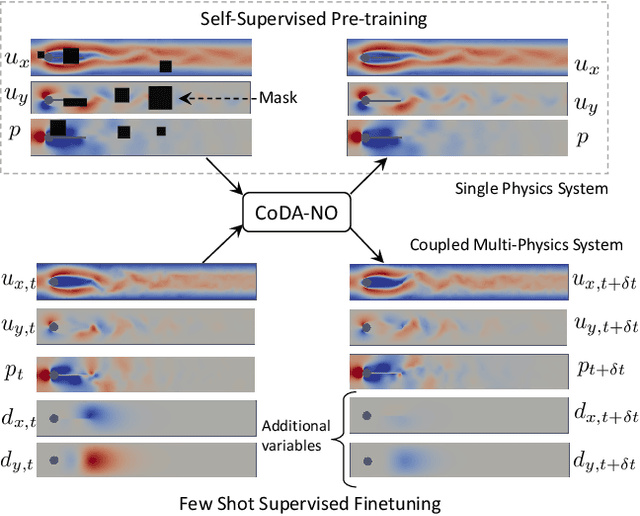

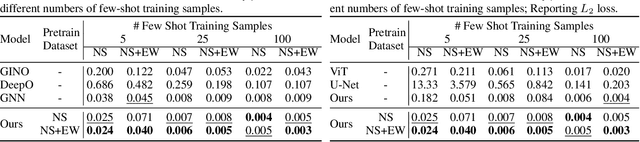
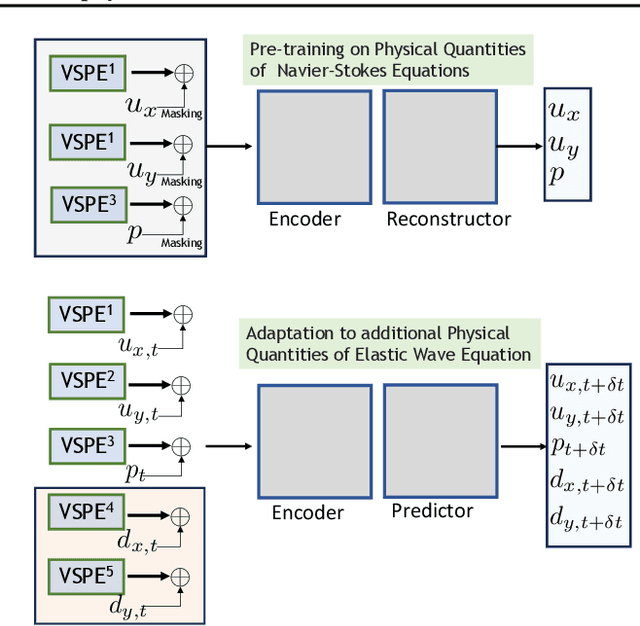
Abstract:Existing neural operator architectures face challenges when solving multiphysics problems with coupled partial differential equations (PDEs), due to complex geometries, interactions between physical variables, and the lack of large amounts of high-resolution training data. To address these issues, we propose Codomain Attention Neural Operator (CoDA-NO), which tokenizes functions along the codomain or channel space, enabling self-supervised learning or pretraining of multiple PDE systems. Specifically, we extend positional encoding, self-attention, and normalization layers to the function space. CoDA-NO can learn representations of different PDE systems with a single model. We evaluate CoDA-NO's potential as a backbone for learning multiphysics PDEs over multiple systems by considering few-shot learning settings. On complex downstream tasks with limited data, such as fluid flow simulations and fluid-structure interactions, we found CoDA-NO to outperform existing methods on the few-shot learning task by over $36\%$. The code is available at https://github.com/ashiq24/CoDA-NO.
Truly Scale-Equivariant Deep Nets with Fourier Layers
Nov 06, 2023Abstract:In computer vision, models must be able to adapt to changes in image resolution to effectively carry out tasks such as image segmentation; This is known as scale-equivariance. Recent works have made progress in developing scale-equivariant convolutional neural networks, e.g., through weight-sharing and kernel resizing. However, these networks are not truly scale-equivariant in practice. Specifically, they do not consider anti-aliasing as they formulate the down-scaling operation in the continuous domain. To address this shortcoming, we directly formulate down-scaling in the discrete domain with consideration of anti-aliasing. We then propose a novel architecture based on Fourier layers to achieve truly scale-equivariant deep nets, i.e., absolute zero equivariance-error. Following prior works, we test this model on MNIST-scale and STL-10 datasets. Our proposed model achieves competitive classification performance while maintaining zero equivariance-error.
Fast Resolution Agnostic Neural Techniques to Solve Partial Differential Equations
Jan 30, 2023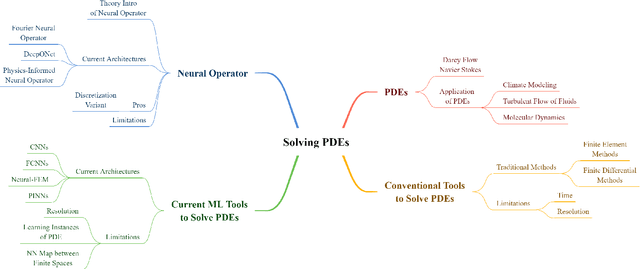



Abstract:Numerical approximations of partial differential equations (PDEs) are routinely employed to formulate the solution of physics, engineering and mathematical problems involving functions of several variables, such as the propagation of heat or sound, fluid flow, elasticity, electrostatics, electrodynamics, and more. While this has led to solving many complex phenomena, there are still significant limitations. Conventional approaches such as Finite Element Methods (FEMs) and Finite Differential Methods (FDMs) require considerable time and are computationally expensive. In contrast, machine learning-based methods such as neural networks are faster once trained, but tend to be restricted to a specific discretization. This article aims to provide a comprehensive summary of conventional methods and recent machine learning-based methods to approximate PDEs numerically. Furthermore, we highlight several key architectures centered around the neural operator, a novel and fast approach (1000x) to learning the solution operator of a PDE. We will note how these new computational approaches can bring immense advantages in tackling many problems in fundamental and applied physics.
PaCMO: Partner Dependent Human Motion Generation in Dyadic Human Activity using Neural Operators
Nov 25, 2022



Abstract:We address the problem of generating 3D human motions in dyadic activities. In contrast to the concurrent works, which mainly focus on generating the motion of a single actor from the textual description, we generate the motion of one of the actors from the motion of the other participating actor in the action. This is a particularly challenging, under-explored problem, that requires learning intricate relationships between the motion of two actors participating in an action and also identifying the action from the motion of one actor. To address these, we propose partner conditioned motion operator (PaCMO), a neural operator-based generative model which learns the distribution of human motion conditioned by the partner's motion in function spaces through adversarial training. Our model can handle long unlabeled action sequences at arbitrary time resolution. We also introduce the "Functional Frechet Inception Distance" ($F^2ID$) metric for capturing similarity between real and generated data for function spaces. We test PaCMO on NTU RGB+D and DuetDance datasets and our model produces realistic results evidenced by the $F^2ID$ score and the conducted user study.
NIO: Lightweight neural operator-based architecture for video frame interpolation
Nov 19, 2022Abstract:We present, NIO - Neural Interpolation Operator, a lightweight efficient neural operator-based architecture to perform video frame interpolation. Current deep learning based methods rely on local convolutions for feature learning and require a large amount of training on comprehensive datasets. Furthermore, transformer-based architectures are large and need dedicated GPUs for training. On the other hand, NIO, our neural operator-based approach learns the features in the frames by translating the image matrix into the Fourier space by using Fast Fourier Transform (FFT). The model performs global convolution, making it discretization invariant. We show that NIO can produce visually-smooth and accurate results and converges in fewer epochs than state-of-the-art approaches. To evaluate the visual quality of our interpolated frames, we calculate the structural similarity index (SSIM) and Peak Signal to Noise Ratio (PSNR) between the generated frame and the ground truth frame. We provide the quantitative performance of our model on Vimeo-90K dataset, DAVIS, UCF101 and DISFA+ dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge