U-NO: U-shaped Neural Operators

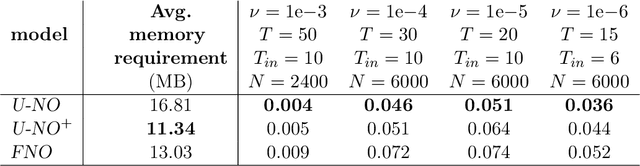
Neural operators generalize classical neural networks to maps between infinite-dimensional spaces, e.g. function spaces. Prior works on neural operators proposed a series of novel architectures to learn such maps and demonstrated unprecedented success in solving partial differential equations (PDEs). In this paper, we propose U-shaped Neural Operators U-NO, an architecture that allows for deeper neural operators compared to prior works. U-NOs exploit the problems structures in function predictions, demonstrate fast training, data efficiency, and robustness w.r.t hyperparameters choices. We study the performance of U-NO on PDE benchmarks, namely, Darcy's flow law and the Navier-Stokes equations. We show that U-NO results in average of 14% and 38% prediction improvement on the Darcy's flow and Navier-Stokes equations, respectively, over the state of art.