5D Neural Surrogates for Nonlinear Gyrokinetic Simulations of Plasma Turbulence

Nuclear fusion plays a pivotal role in the quest for reliable and sustainable energy production. A major roadblock to achieving commercially viable fusion power is understanding plasma turbulence, which can significantly degrade plasma confinement. Modelling turbulence is crucial to design performing plasma scenarios for next-generation reactor-class devices and current experimental machines. The nonlinear gyrokinetic equation underpinning turbulence modelling evolves a 5D distribution function over time. Solving this equation numerically is extremely expensive, requiring up to weeks for a single run to converge, making it unfeasible for iterative optimisation and control studies. In this work, we propose a method for training neural surrogates for 5D gyrokinetic simulations. Our method extends a hierarchical vision transformer to five dimensions and is trained on the 5D distribution function for the adiabatic electron approximation. We demonstrate that our model can accurately infer downstream physical quantities such as heat flux time trace and electrostatic potentials for single-step predictions two orders of magnitude faster than numerical codes. Our work paves the way towards neural surrogates for plasma turbulence simulations to accelerate deployment of commercial energy production via nuclear fusion.

Calibrated Physics-Informed Uncertainty Quantification

Neural PDEs offer efficient alternatives to computationally expensive numerical PDE solvers for simulating complex physical systems. However, their lack of robust uncertainty quantification (UQ) limits deployment in critical applications. We introduce a model-agnostic, physics-informed conformal prediction (CP) framework that provides guaranteed uncertainty estimates without requiring labelled data. By utilising a physics-based approach, we are able to quantify and calibrate the model's inconsistencies with the PDE rather than the uncertainty arising from the data. Our approach uses convolutional layers as finite-difference stencils and leverages physics residual errors as nonconformity scores, enabling data-free UQ with marginal and joint coverage guarantees across prediction domains for a range of complex PDEs. We further validate the efficacy of our method on neural PDE models for plasma modelling and shot design in fusion reactors.

Uncertainty Quantification of Pre-Trained and Fine-Tuned Surrogate Models using Conformal Prediction

Data-driven surrogate models have shown immense potential as quick, inexpensive approximations to complex numerical and experimental modelling tasks. However, most surrogate models characterising physical systems do not quantify their uncertainty, rendering their predictions unreliable, and needing further validation. Though Bayesian approximations offer some solace in estimating the error associated with these models, they cannot provide they cannot provide guarantees, and the quality of their inferences depends on the availability of prior information and good approximations to posteriors for complex problems. This is particularly pertinent to multi-variable or spatio-temporal problems. Our work constructs and formalises a conformal prediction framework that satisfies marginal coverage for spatio-temporal predictions in a model-agnostic manner, requiring near-zero computational costs. The paper provides an extensive empirical study of the application of the framework to ascertain valid error bars that provide guaranteed coverage across the surrogate model's domain of operation. The application scope of our work extends across a large range of spatio-temporal models, ranging from solving partial differential equations to weather forecasting. Through the applications, the paper looks at providing statistically valid error bars for deterministic models, as well as crafting guarantees to the error bars of probabilistic models. The paper concludes with a viable conformal prediction formalisation that provides guaranteed coverage of the surrogate model, regardless of model architecture, and its training regime and is unbothered by the curse of dimensionality.

Valid Error Bars for Neural Weather Models using Conformal Prediction

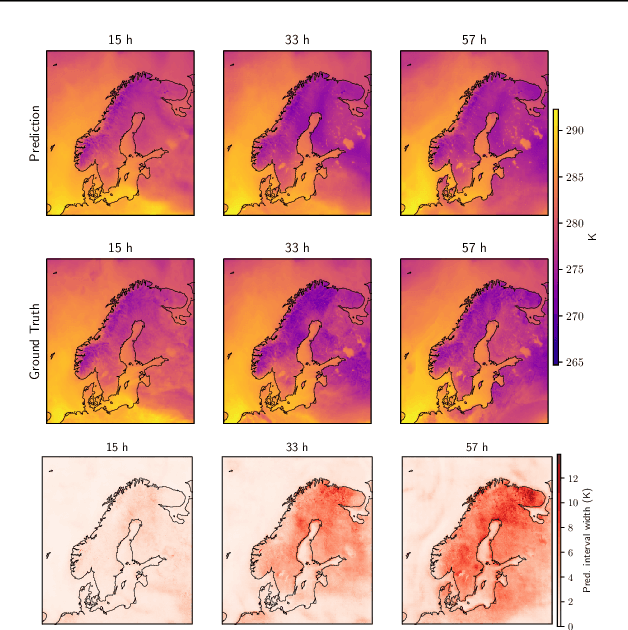
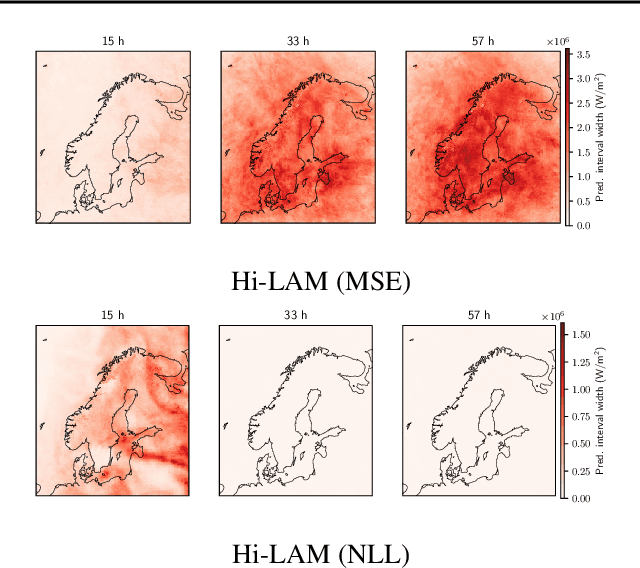
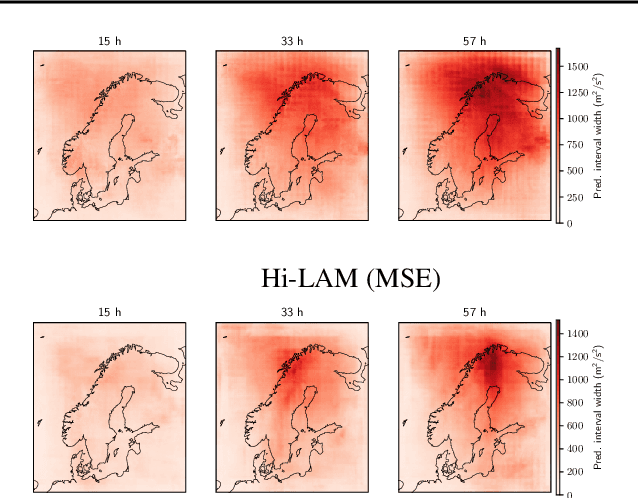
Neural weather models have shown immense potential as inexpensive and accurate alternatives to physics-based models. However, most models trained to perform weather forecasting do not quantify the uncertainty associated with their forecasts. This limits the trust in the model and the usefulness of the forecasts. In this work we construct and formalise a conformal prediction framework as a post-processing method for estimating this uncertainty. The method is model-agnostic and gives calibrated error bounds for all variables, lead times and spatial locations. No modifications are required to the model and the computational cost is negligible compared to model training. We demonstrate the usefulness of the conformal prediction framework on a limited area neural weather model for the Nordic region. We further explore the advantages of the framework for deterministic and probabilistic models.

Plasma Surrogate Modelling using Fourier Neural Operators

Predicting plasma evolution within a Tokamak reactor is crucial to realizing the goal of sustainable fusion. Capabilities in forecasting the spatio-temporal evolution of plasma rapidly and accurately allow us to quickly iterate over design and control strategies on current Tokamak devices and future reactors. Modelling plasma evolution using numerical solvers is often expensive, consuming many hours on supercomputers, and hence, we need alternative inexpensive surrogate models. We demonstrate accurate predictions of plasma evolution both in simulation and experimental domains using deep learning-based surrogate modelling tools, viz., Fourier Neural Operators (FNO). We show that FNO has a speedup of six orders of magnitude over traditional solvers in predicting the plasma dynamics simulated from magnetohydrodynamic models, while maintaining a high accuracy (MSE $\approx$ $10^{-5}$). Our modified version of the FNO is capable of solving multi-variable Partial Differential Equations (PDE), and can capture the dependence among the different variables in a single model. FNOs can also predict plasma evolution on real-world experimental data observed by the cameras positioned within the MAST Tokamak, i.e., cameras looking across the central solenoid and the divertor in the Tokamak. We show that FNOs are able to accurately forecast the evolution of plasma and have the potential to be deployed for real-time monitoring. We also illustrate their capability in forecasting the plasma shape, the locations of interactions of the plasma with the central solenoid and the divertor for the full duration of the plasma shot within MAST. The FNO offers a viable alternative for surrogate modelling as it is quick to train and infer, and requires fewer data points, while being able to do zero-shot super-resolution and getting high-fidelity solutions.

Fourier-RNNs for Modelling Noisy Physics Data

Classical sequential models employed in time-series prediction rely on learning the mappings from the past to the future instances by way of a hidden state. The Hidden states characterise the historical information and encode the required temporal dependencies. However, most existing sequential models operate within finite-dimensional Euclidean spaces which offer limited functionality when employed in modelling physics relevant data. Alternatively recent work with neural operator learning within the Fourier space has shown efficient strategies for parameterising Partial Differential Equations (PDE). In this work, we propose a novel sequential model, built to handle Physics relevant data by way of amalgamating the conventional RNN architecture with that of the Fourier Neural Operators (FNO). The Fourier-RNN allows for learning the mappings from the input to the output as well as to the hidden state within the Fourier space associated with the temporal data. While the Fourier-RNN performs identical to the FNO when handling PDE data, it outperforms the FNO and the conventional RNN when deployed in modelling noisy, non-Markovian data.