Valid Error Bars for Neural Weather Models using Conformal Prediction

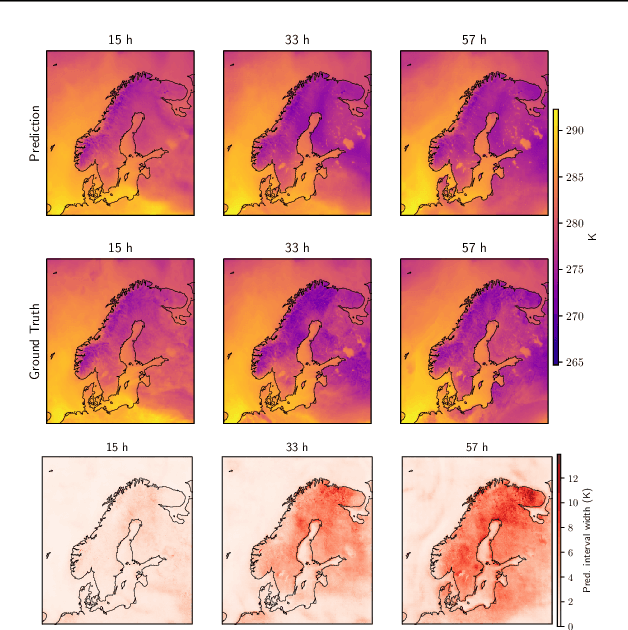
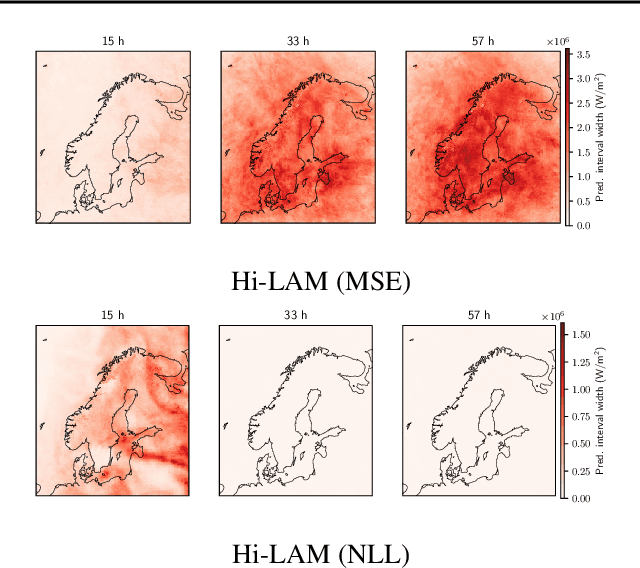
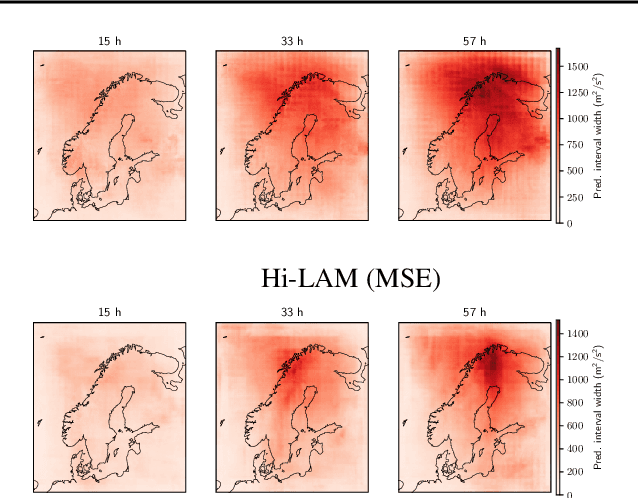
Neural weather models have shown immense potential as inexpensive and accurate alternatives to physics-based models. However, most models trained to perform weather forecasting do not quantify the uncertainty associated with their forecasts. This limits the trust in the model and the usefulness of the forecasts. In this work we construct and formalise a conformal prediction framework as a post-processing method for estimating this uncertainty. The method is model-agnostic and gives calibrated error bounds for all variables, lead times and spatial locations. No modifications are required to the model and the computational cost is negligible compared to model training. We demonstrate the usefulness of the conformal prediction framework on a limited area neural weather model for the Nordic region. We further explore the advantages of the framework for deterministic and probabilistic models.

Understanding Deep Generative Models with Generalized Empirical Likelihoods

Understanding how well a deep generative model captures a distribution of high-dimensional data remains an important open challenge. It is especially difficult for certain model classes, such as Generative Adversarial Networks and Diffusion Models, whose models do not admit exact likelihoods. In this work, we demonstrate that generalized empirical likelihood (GEL) methods offer a family of diagnostic tools that can identify many deficiencies of deep generative models (DGMs). We show, with appropriate specification of moment conditions, that the proposed method can identify which modes have been dropped, the degree to which DGMs are mode imbalanced, and whether DGMs sufficiently capture intra-class diversity. We show how to combine techniques from Maximum Mean Discrepancy and Generalized Empirical Likelihood to create not only distribution tests that retain per-sample interpretability, but also metrics that include label information. We find that such tests predict the degree of mode dropping and mode imbalance up to 60% better than metrics such as improved precision/recall.

Copula Flows for Synthetic Data Generation

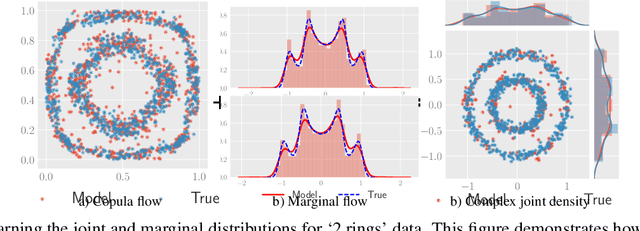
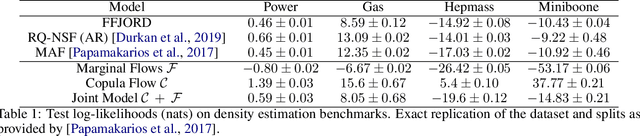
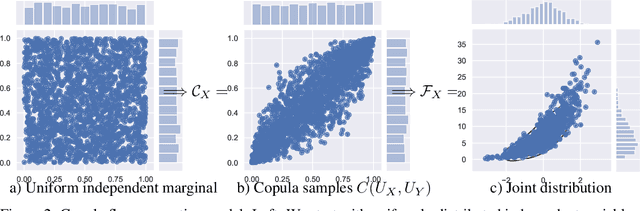
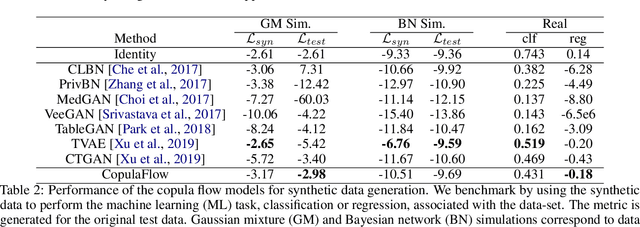
The ability to generate high-fidelity synthetic data is crucial when available (real) data is limited or where privacy and data protection standards allow only for limited use of the given data, e.g., in medical and financial data-sets. Current state-of-the-art methods for synthetic data generation are based on generative models, such as Generative Adversarial Networks (GANs). Even though GANs have achieved remarkable results in synthetic data generation, they are often challenging to interpret.Furthermore, GAN-based methods can suffer when used with mixed real and categorical variables.Moreover, loss function (discriminator loss) design itself is problem specific, i.e., the generative model may not be useful for tasks it was not explicitly trained for. In this paper, we propose to use a probabilistic model as a synthetic data generator. Learning the probabilistic model for the data is equivalent to estimating the density of the data. Based on the copula theory, we divide the density estimation task into two parts, i.e., estimating univariate marginals and estimating the multivariate copula density over the univariate marginals. We use normalising flows to learn both the copula density and univariate marginals. We benchmark our method on both simulated and real data-sets in terms of density estimation as well as the ability to generate high-fidelity synthetic data

Gaussian Process Conditional Density Estimation

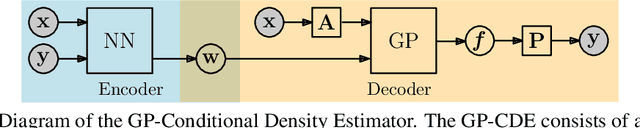
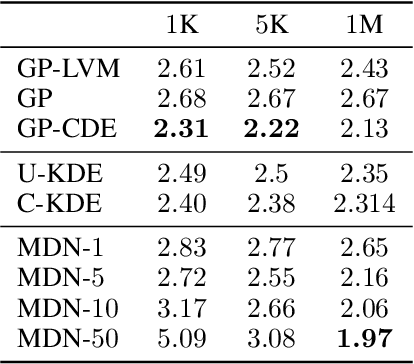
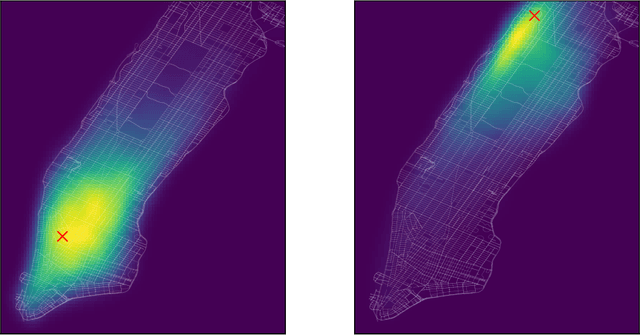
Conditional Density Estimation (CDE) models deal with estimating conditional distributions. The conditions imposed on the distribution are the inputs of the model. CDE is a challenging task as there is a fundamental trade-off between model complexity, representational capacity and overfitting. In this work, we propose to extend the model's input with latent variables and use Gaussian processes (GP) to map this augmented input onto samples from the conditional distribution. Our Bayesian approach allows for the modeling of small datasets, but we also provide the machinery for it to be applied to big data using stochastic variational inference. Our approach can be used to model densities even in sparse data regions, and allows for sharing learned structure between conditions. We illustrate the effectiveness and wide-reaching applicability of our model on a variety of real-world problems, such as spatio-temporal density estimation of taxi drop-offs, non-Gaussian noise modeling, and few-shot learning on omniglot images.

Orthogonally Decoupled Variational Gaussian Processes

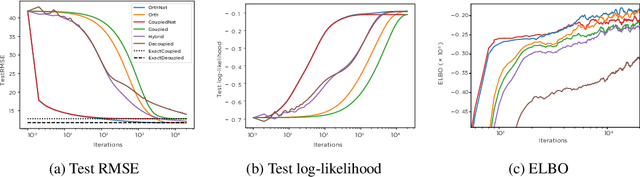
Gaussian processes (GPs) provide a powerful non-parametric framework for reasoning over functions. Despite appealing theory, its superlinear computational and memory complexities have presented a long-standing challenge. State-of-the-art sparse variational inference methods trade modeling accuracy against complexity. However, the complexities of these methods still scale superlinearly in the number of basis functions, implying that that sparse GP methods are able to learn from large datasets only when a small model is used. Recently, a decoupled approach was proposed that removes the unnecessary coupling between the complexities of modeling the mean and the covariance functions of a GP. It achieves a linear complexity in the number of mean parameters, so an expressive posterior mean function can be modeled. While promising, this approach suffers from optimization difficulties due to ill-conditioning and non-convexity. In this work, we propose an alternative decoupled parametrization. It adopts an orthogonal basis in the mean function to model the residues that cannot be learned by the standard coupled approach. Therefore, our method extends, rather than replaces, the coupled approach to achieve strictly better performance. This construction admits a straightforward natural gradient update rule, so the structure of the information manifold that is lost during decoupling can be leveraged to speed up learning. Empirically, our algorithm demonstrates significantly faster convergence in multiple experiments.

Doubly Stochastic Variational Inference for Deep Gaussian Processes

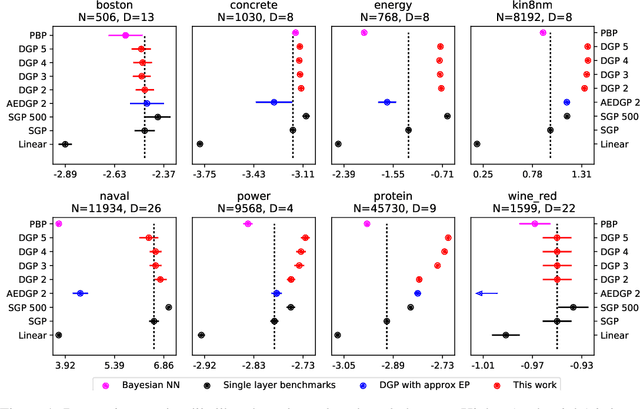
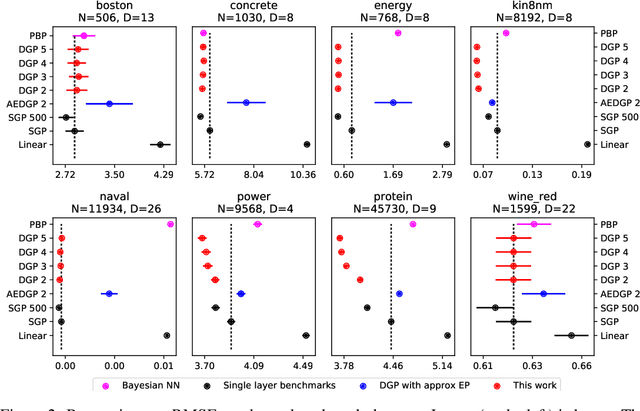
Gaussian processes (GPs) are a good choice for function approximation as they are flexible, robust to over-fitting, and provide well-calibrated predictive uncertainty. Deep Gaussian processes (DGPs) are multi-layer generalisations of GPs, but inference in these models has proved challenging. Existing approaches to inference in DGP models assume approximate posteriors that force independence between the layers, and do not work well in practice. We present a doubly stochastic variational inference algorithm, which does not force independence between layers. With our method of inference we demonstrate that a DGP model can be used effectively on data ranging in size from hundreds to a billion points. We provide strong empirical evidence that our inference scheme for DGPs works well in practice in both classification and regression.