GPflux: A Library for Deep Gaussian Processes

We introduce GPflux, a Python library for Bayesian deep learning with a strong emphasis on deep Gaussian processes (DGPs). Implementing DGPs is a challenging endeavour due to the various mathematical subtleties that arise when dealing with multivariate Gaussian distributions and the complex bookkeeping of indices. To date, there are no actively maintained, open-sourced and extendable libraries available that support research activities in this area. GPflux aims to fill this gap by providing a library with state-of-the-art DGP algorithms, as well as building blocks for implementing novel Bayesian and GP-based hierarchical models and inference schemes. GPflux is compatible with and built on top of the Keras deep learning eco-system. This enables practitioners to leverage tools from the deep learning community for building and training customised Bayesian models, and create hierarchical models that consist of Bayesian and standard neural network layers in a single coherent framework. GPflux relies on GPflow for most of its GP objects and operations, which makes it an efficient, modular and extensible library, while having a lean codebase.

Stochastic Differential Equations with Variational Wishart Diffusions

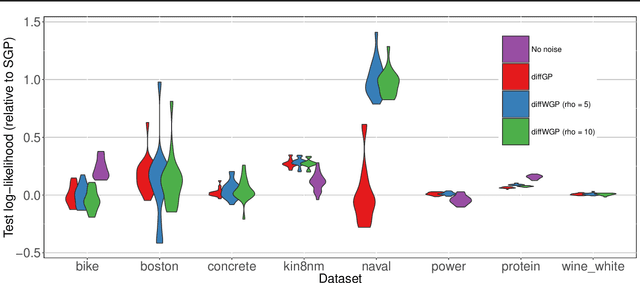
We present a Bayesian non-parametric way of inferring stochastic differential equations for both regression tasks and continuous-time dynamical modelling. The work has high emphasis on the stochastic part of the differential equation, also known as the diffusion, and modelling it by means of Wishart processes. Further, we present a semi-parametric approach that allows the framework to scale to high dimensions. This successfully lead us onto how to model both latent and auto-regressive temporal systems with conditional heteroskedastic noise. We provide experimental evidence that modelling diffusion often improves performance and that this randomness in the differential equation can be essential to avoid overfitting.

Deep Gaussian Processes with Importance-Weighted Variational Inference

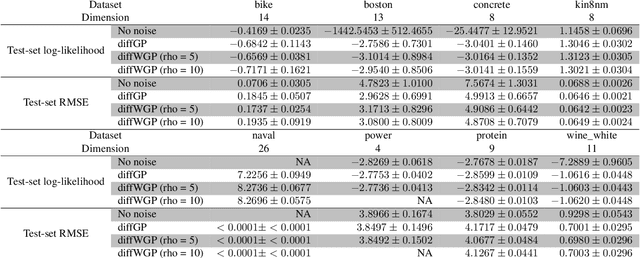
Deep Gaussian processes (DGPs) can model complex marginal densities as well as complex mappings. Non-Gaussian marginals are essential for modelling real-world data, and can be generated from the DGP by incorporating uncorrelated variables to the model. Previous work on DGP models has introduced noise additively and used variational inference with a combination of sparse Gaussian processes and mean-field Gaussians for the approximate posterior. Additive noise attenuates the signal, and the Gaussian form of variational distribution may lead to an inaccurate posterior. We instead incorporate noisy variables as latent covariates, and propose a novel importance-weighted objective, which leverages analytic results and provides a mechanism to trade off computation for improved accuracy. Our results demonstrate that the importance-weighted objective works well in practice and consistently outperforms classical variational inference, especially for deeper models.

Gaussian Process Conditional Density Estimation

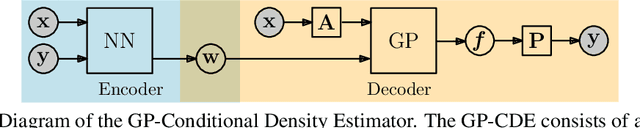
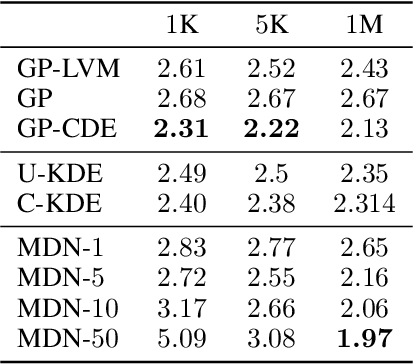
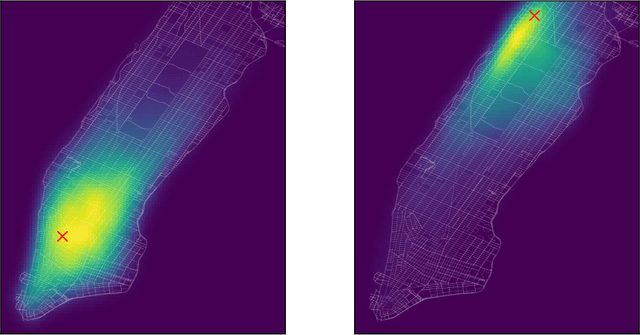
Conditional Density Estimation (CDE) models deal with estimating conditional distributions. The conditions imposed on the distribution are the inputs of the model. CDE is a challenging task as there is a fundamental trade-off between model complexity, representational capacity and overfitting. In this work, we propose to extend the model's input with latent variables and use Gaussian processes (GP) to map this augmented input onto samples from the conditional distribution. Our Bayesian approach allows for the modeling of small datasets, but we also provide the machinery for it to be applied to big data using stochastic variational inference. Our approach can be used to model densities even in sparse data regions, and allows for sharing learned structure between conditions. We illustrate the effectiveness and wide-reaching applicability of our model on a variety of real-world problems, such as spatio-temporal density estimation of taxi drop-offs, non-Gaussian noise modeling, and few-shot learning on omniglot images.

Orthogonally Decoupled Variational Gaussian Processes

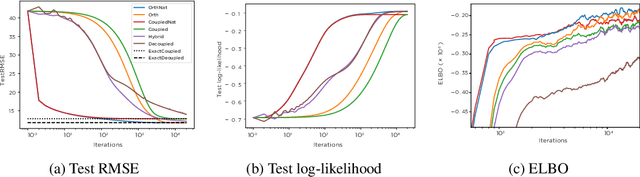
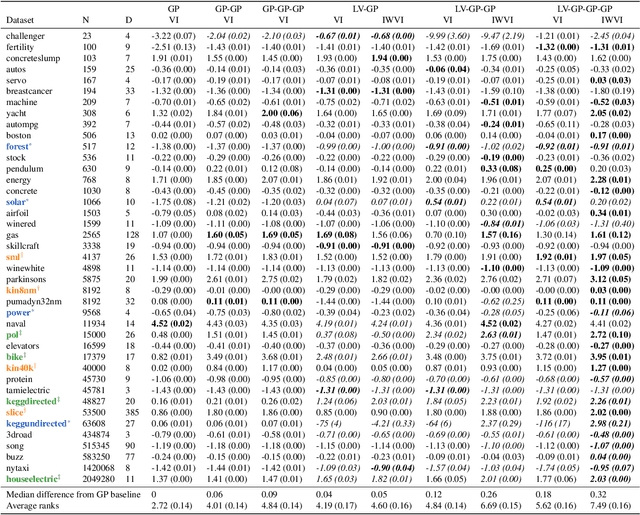
Gaussian processes (GPs) provide a powerful non-parametric framework for reasoning over functions. Despite appealing theory, its superlinear computational and memory complexities have presented a long-standing challenge. State-of-the-art sparse variational inference methods trade modeling accuracy against complexity. However, the complexities of these methods still scale superlinearly in the number of basis functions, implying that that sparse GP methods are able to learn from large datasets only when a small model is used. Recently, a decoupled approach was proposed that removes the unnecessary coupling between the complexities of modeling the mean and the covariance functions of a GP. It achieves a linear complexity in the number of mean parameters, so an expressive posterior mean function can be modeled. While promising, this approach suffers from optimization difficulties due to ill-conditioning and non-convexity. In this work, we propose an alternative decoupled parametrization. It adopts an orthogonal basis in the mean function to model the residues that cannot be learned by the standard coupled approach. Therefore, our method extends, rather than replaces, the coupled approach to achieve strictly better performance. This construction admits a straightforward natural gradient update rule, so the structure of the information manifold that is lost during decoupling can be leveraged to speed up learning. Empirically, our algorithm demonstrates significantly faster convergence in multiple experiments.

Natural Gradients in Practice: Non-Conjugate Variational Inference in Gaussian Process Models

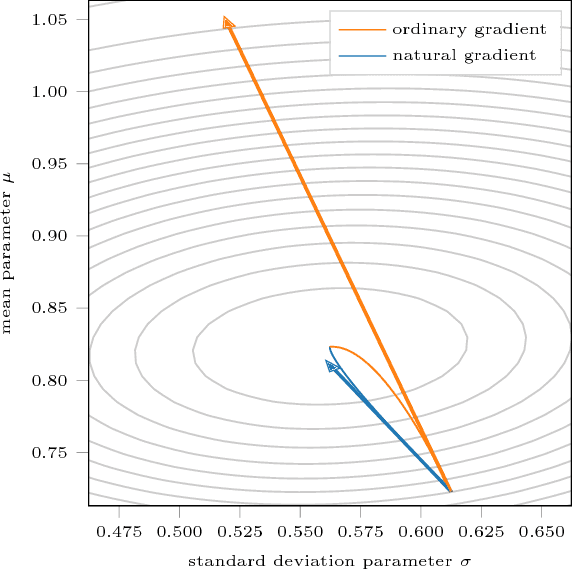
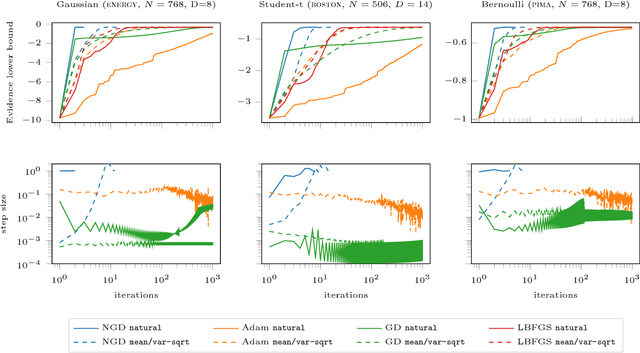
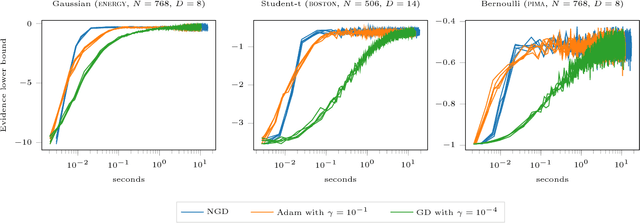
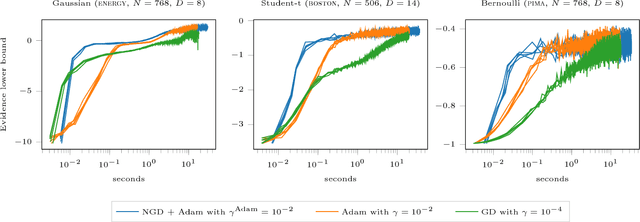
The natural gradient method has been used effectively in conjugate Gaussian process models, but the non-conjugate case has been largely unexplored. We examine how natural gradients can be used in non-conjugate stochastic settings, together with hyperparameter learning. We conclude that the natural gradient can significantly improve performance in terms of wall-clock time. For ill-conditioned posteriors the benefit of the natural gradient method is especially pronounced, and we demonstrate a practical setting where ordinary gradients are unusable. We show how natural gradients can be computed efficiently and automatically in any parameterization, using automatic differentiation. Our code is integrated into the GPflow package.

Doubly Stochastic Variational Inference for Deep Gaussian Processes

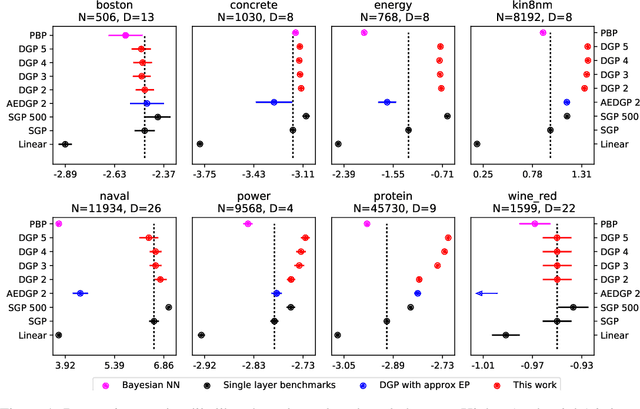
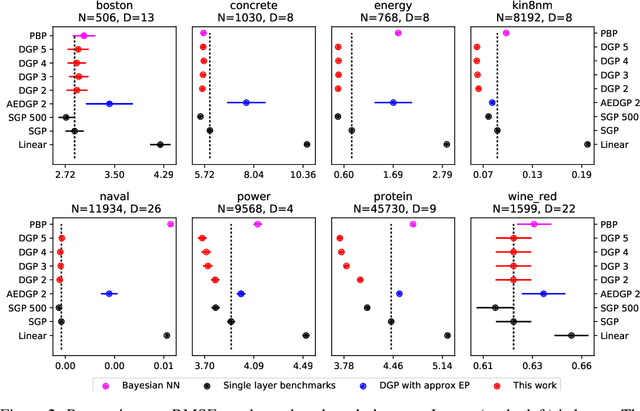
Gaussian processes (GPs) are a good choice for function approximation as they are flexible, robust to over-fitting, and provide well-calibrated predictive uncertainty. Deep Gaussian processes (DGPs) are multi-layer generalisations of GPs, but inference in these models has proved challenging. Existing approaches to inference in DGP models assume approximate posteriors that force independence between the layers, and do not work well in practice. We present a doubly stochastic variational inference algorithm, which does not force independence between layers. With our method of inference we demonstrate that a DGP model can be used effectively on data ranging in size from hundreds to a billion points. We provide strong empirical evidence that our inference scheme for DGPs works well in practice in both classification and regression.

Deep Unsupervised Clustering with Gaussian Mixture Variational Autoencoders

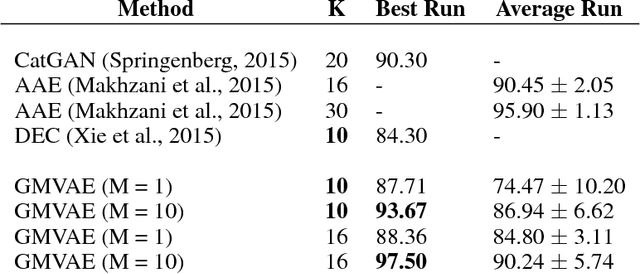
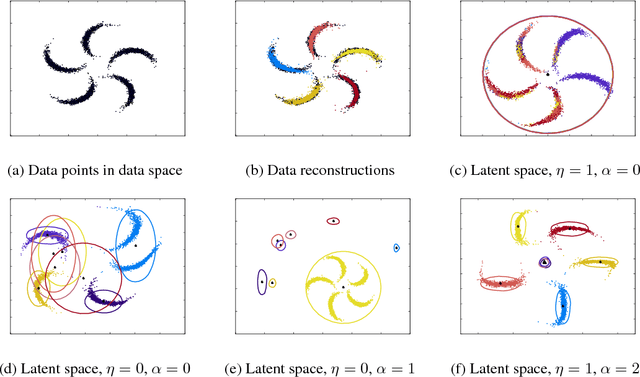
We study a variant of the variational autoencoder model (VAE) with a Gaussian mixture as a prior distribution, with the goal of performing unsupervised clustering through deep generative models. We observe that the known problem of over-regularisation that has been shown to arise in regular VAEs also manifests itself in our model and leads to cluster degeneracy. We show that a heuristic called minimum information constraint that has been shown to mitigate this effect in VAEs can also be applied to improve unsupervised clustering performance with our model. Furthermore we analyse the effect of this heuristic and provide an intuition of the various processes with the help of visualizations. Finally, we demonstrate the performance of our model on synthetic data, MNIST and SVHN, showing that the obtained clusters are distinct, interpretable and result in achieving competitive performance on unsupervised clustering to the state-of-the-art results.