Challenges in interpretability of additive models

We review generalized additive models as a type of ``transparent'' model that has recently seen renewed interest in the deep learning community as neural additive models. We highlight multiple types of nonidentifiability in this model class and discuss challenges in interpretability, arguing for restraint when claiming ``interpretability'' or ``suitability for safety-critical applications'' of such models.

Identifying latent state transition in non-linear dynamical systems

This work aims to improve generalization and interpretability of dynamical systems by recovering the underlying lower-dimensional latent states and their time evolutions. Previous work on disentangled representation learning within the realm of dynamical systems focused on the latent states, possibly with linear transition approximations. As such, they cannot identify nonlinear transition dynamics, and hence fail to reliably predict complex future behavior. Inspired by the advances in nonlinear ICA, we propose a state-space modeling framework in which we can identify not just the latent states but also the unknown transition function that maps the past states to the present. We introduce a practical algorithm based on variational auto-encoders and empirically demonstrate in realistic synthetic settings that we can (i) recover latent state dynamics with high accuracy, (ii) correspondingly achieve high future prediction accuracy, and (iii) adapt fast to new environments.

Nonparametric modeling of the composite effect of multiple nutrients on blood glucose dynamics

In biomedical applications it is often necessary to estimate a physiological response to a treatment consisting of multiple components, and learn the separate effects of the components in addition to the joint effect. Here, we extend existing probabilistic nonparametric approaches to explicitly address this problem. We also develop a new convolution-based model for composite treatment-response curves that is more biologically interpretable. We validate our models by estimating the impact of carbohydrate and fat in meals on blood glucose. By differentiating treatment components, incorporating their dosages, and sharing statistical information across patients via a hierarchical multi-output Gaussian process, our method improves prediction accuracy over existing approaches, and allows us to interpret the different effects of carbohydrates and fat on the overall glucose response.

Thin and Deep Gaussian Processes

Gaussian processes (GPs) can provide a principled approach to uncertainty quantification with easy-to-interpret kernel hyperparameters, such as the lengthscale, which controls the correlation distance of function values. However, selecting an appropriate kernel can be challenging. Deep GPs avoid manual kernel engineering by successively parameterizing kernels with GP layers, allowing them to learn low-dimensional embeddings of the inputs that explain the output data. Following the architecture of deep neural networks, the most common deep GPs warp the input space layer-by-layer but lose all the interpretability of shallow GPs. An alternative construction is to successively parameterize the lengthscale of a kernel, improving the interpretability but ultimately giving away the notion of learning lower-dimensional embeddings. Unfortunately, both methods are susceptible to particular pathologies which may hinder fitting and limit their interpretability. This work proposes a novel synthesis of both previous approaches: Thin and Deep GP (TDGP). Each TDGP layer defines locally linear transformations of the original input data maintaining the concept of latent embeddings while also retaining the interpretation of lengthscales of a kernel. Moreover, unlike the prior solutions, TDGP induces non-pathological manifolds that admit learning lower-dimensional representations. We show with theoretical and experimental results that i) TDGP is, unlike previous models, tailored to specifically discover lower-dimensional manifolds in the input data, ii) TDGP behaves well when increasing the number of layers, and iii) TDGP performs well in standard benchmark datasets.

Beyond Intuition, a Framework for Applying GPs to Real-World Data

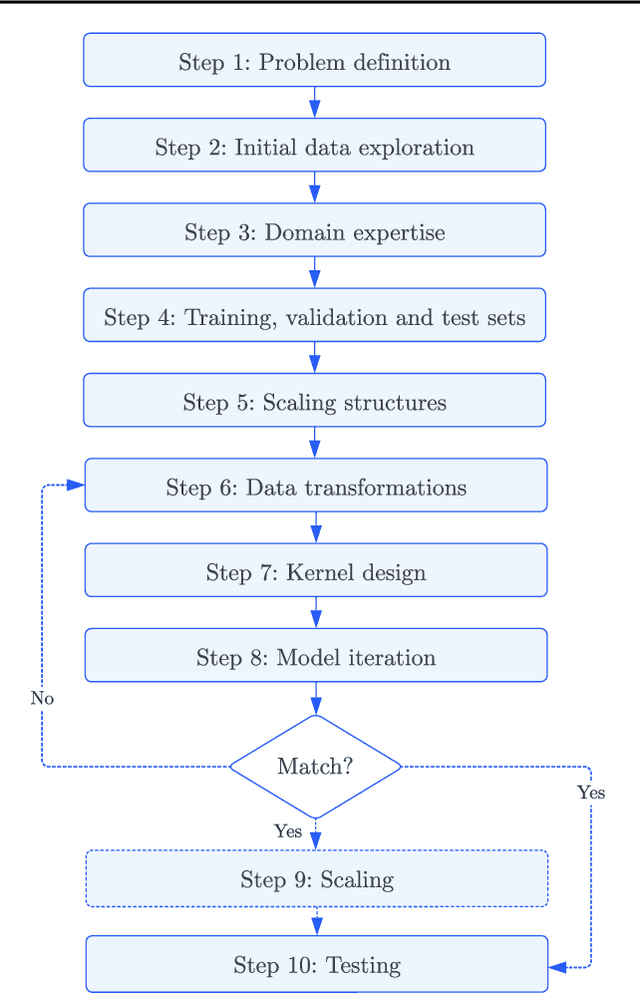
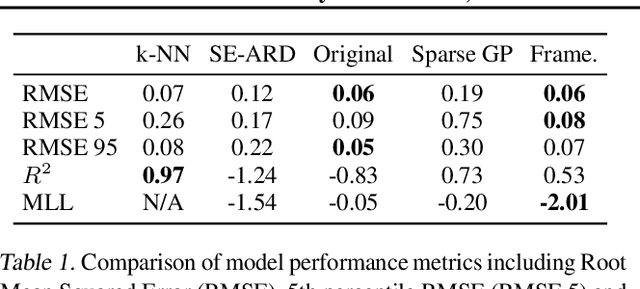
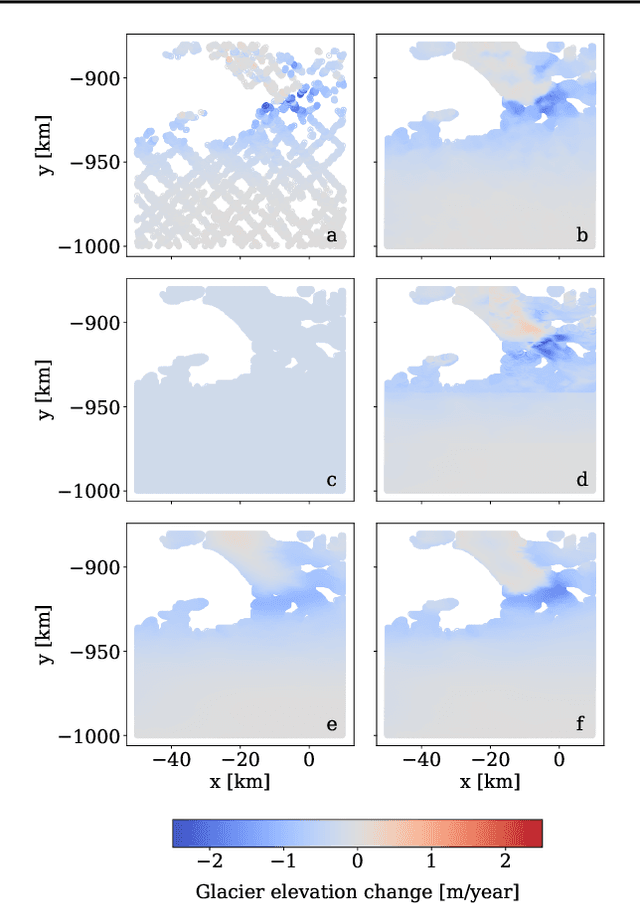
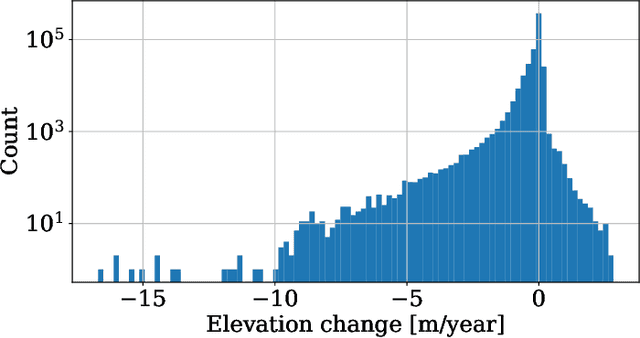
Gaussian Processes (GPs) offer an attractive method for regression over small, structured and correlated datasets. However, their deployment is hindered by computational costs and limited guidelines on how to apply GPs beyond simple low-dimensional datasets. We propose a framework to identify the suitability of GPs to a given problem and how to set up a robust and well-specified GP model. The guidelines formalise the decisions of experienced GP practitioners, with an emphasis on kernel design and options for computational scalability. The framework is then applied to a case study of glacier elevation change yielding more accurate results at test time.

Practical Equivariances via Relational Conditional Neural Processes

Conditional Neural Processes (CNPs) are a class of metalearning models popular for combining the runtime efficiency of amortized inference with reliable uncertainty quantification. Many relevant machine learning tasks, such as spatio-temporal modeling, Bayesian Optimization and continuous control, contain equivariances -- for example to translation -- which the model can exploit for maximal performance. However, prior attempts to include equivariances in CNPs do not scale effectively beyond two input dimensions. In this work, we propose Relational Conditional Neural Processes (RCNPs), an effective approach to incorporate equivariances into any neural process model. Our proposed method extends the applicability and impact of equivariant neural processes to higher dimensions. We empirically demonstrate the competitive performance of RCNPs on a large array of tasks naturally containing equivariances.

Temporal Causal Mediation through a Point Process: Direct and Indirect Effects of Healthcare Interventions

Deciding on an appropriate intervention requires a causal model of a treatment, the outcome, and potential mediators. Causal mediation analysis lets us distinguish between direct and indirect effects of the intervention, but has mostly been studied in a static setting. In healthcare, data come in the form of complex, irregularly sampled time-series, with dynamic interdependencies between a treatment, outcomes, and mediators across time. Existing approaches to dynamic causal mediation analysis are limited to regular measurement intervals, simple parametric models, and disregard long-range mediator--outcome interactions. To address these limitations, we propose a non-parametric mediator--outcome model where the mediator is assumed to be a temporal point process that interacts with the outcome process. With this model, we estimate the direct and indirect effects of an external intervention on the outcome, showing how each of these affects the whole future trajectory. We demonstrate on semi-synthetic data that our method can accurately estimate direct and indirect effects. On real-world healthcare data, our model infers clinically meaningful direct and indirect effect trajectories for blood glucose after a surgery.

Improving Hyperparameter Learning under Approximate Inference in Gaussian Process Models

Approximate inference in Gaussian process (GP) models with non-conjugate likelihoods gets entangled with the learning of the model hyperparameters. We improve hyperparameter learning in GP models and focus on the interplay between variational inference (VI) and the learning target. While VI's lower bound to the marginal likelihood is a suitable objective for inferring the approximate posterior, we show that a direct approximation of the marginal likelihood as in Expectation Propagation (EP) is a better learning objective for hyperparameter optimization. We design a hybrid training procedure to bring the best of both worlds: it leverages conjugate-computation VI for inference and uses an EP-like marginal likelihood approximation for hyperparameter learning. We compare VI, EP, Laplace approximation, and our proposed training procedure and empirically demonstrate the effectiveness of our proposal across a wide range of data sets.

Towards Improved Learning in Gaussian Processes: The Best of Two Worlds

Gaussian process training decomposes into inference of the (approximate) posterior and learning of the hyperparameters. For non-Gaussian (non-conjugate) likelihoods, two common choices for approximate inference are Expectation Propagation (EP) and Variational Inference (VI), which have complementary strengths and weaknesses. While VI's lower bound to the marginal likelihood is a suitable objective for inferring the approximate posterior, it does not automatically imply it is a good learning objective for hyperparameter optimization. We design a hybrid training procedure where the inference leverages conjugate-computation VI and the learning uses an EP-like marginal likelihood approximation. We empirically demonstrate on binary classification that this provides a good learning objective and generalizes better.

Fantasizing with Dual GPs in Bayesian Optimization and Active Learning

Gaussian processes (GPs) are the main surrogate functions used for sequential modelling such as Bayesian Optimization and Active Learning. Their drawbacks are poor scaling with data and the need to run an optimization loop when using a non-Gaussian likelihood. In this paper, we focus on `fantasizing' batch acquisition functions that need the ability to condition on new fantasized data computationally efficiently. By using a sparse Dual GP parameterization, we gain linear scaling with batch size as well as one-step updates for non-Gaussian likelihoods, thus extending sparse models to greedy batch fantasizing acquisition functions.