Latent variable model for high-dimensional point process with structured missingness

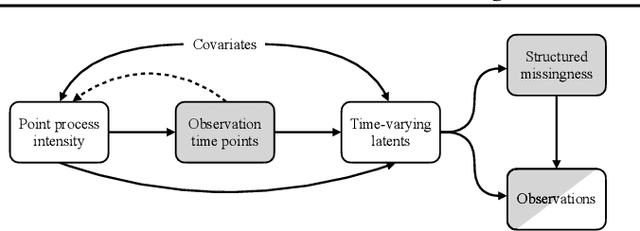
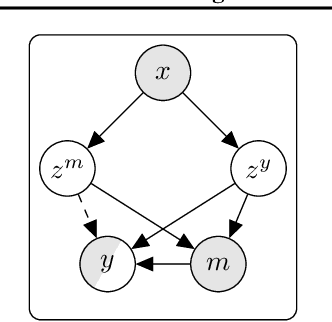
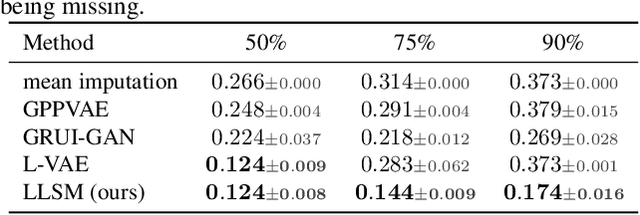
Longitudinal data are important in numerous fields, such as healthcare, sociology and seismology, but real-world datasets present notable challenges for practitioners because they can be high-dimensional, contain structured missingness patterns, and measurement time points can be governed by an unknown stochastic process. While various solutions have been suggested, the majority of them have been designed to account for only one of these challenges. In this work, we propose a flexible and efficient latent-variable model that is capable of addressing all these limitations. Our approach utilizes Gaussian processes to capture temporal correlations between samples and their associated missingness masks as well as to model the underlying point process. We construct our model as a variational autoencoder together with deep neural network parameterised encoder and decoder models, and develop a scalable amortised variational inference approach for efficient model training. We demonstrate competitive performance using both simulated and real datasets.

Estimating treatment effects from single-arm trials via latent-variable modeling

Randomized controlled trials (RCTs) are the accepted standard for treatment effect estimation but they can be infeasible due to ethical reasons and prohibitive costs. Single-arm trials, where all patients belong to the treatment group, can be a viable alternative but require access to an external control group. We propose an identifiable deep latent-variable model for this scenario that can also account for missing covariate observations by modeling their structured missingness patterns. Our method uses amortized variational inference to learn both group-specific and identifiable shared latent representations, which can subsequently be used for (i) patient matching if treatment outcomes are not available for the treatment group, or for (ii) direct treatment effect estimation assuming outcomes are available for both groups. We evaluate the model on a public benchmark as well as on a data set consisting of a published RCT study and real-world electronic health records. Compared to previous methods, our results show improved performance both for direct treatment effect estimation as well as for effect estimation via patient matching.

Practical Equivariances via Relational Conditional Neural Processes

Conditional Neural Processes (CNPs) are a class of metalearning models popular for combining the runtime efficiency of amortized inference with reliable uncertainty quantification. Many relevant machine learning tasks, such as spatio-temporal modeling, Bayesian Optimization and continuous control, contain equivariances -- for example to translation -- which the model can exploit for maximal performance. However, prior attempts to include equivariances in CNPs do not scale effectively beyond two input dimensions. In this work, we propose Relational Conditional Neural Processes (RCNPs), an effective approach to incorporate equivariances into any neural process model. Our proposed method extends the applicability and impact of equivariant neural processes to higher dimensions. We empirically demonstrate the competitive performance of RCNPs on a large array of tasks naturally containing equivariances.

Evidential Turing Processes

A probabilistic classifier with reliable predictive uncertainties i) fits successfully to the target domain data, ii) provides calibrated class probabilities in difficult regions of the target domain (e.g. class overlap), and iii) accurately identifies queries coming out of the target domain and reject them. We introduce an original combination of evidential deep learning, neural processes, and neural Turing machines capable of providing all three essential properties mentioned above for total uncertainty quantification. We observe our method on three image classification benchmarks and two neural net architectures to consistently give competitive or superior scores with respect to multiple uncertainty quantification metrics against state-of-the-art methods explicitly tailored to one or a few of them. Our unified solution delivers an implementation-friendly and computationally efficient recipe for safety clearance and provides intellectual economy to an investigation of algorithmic roots of epistemic awareness in deep neural nets.

Learning Partially Known Stochastic Dynamics with Empirical PAC Bayes

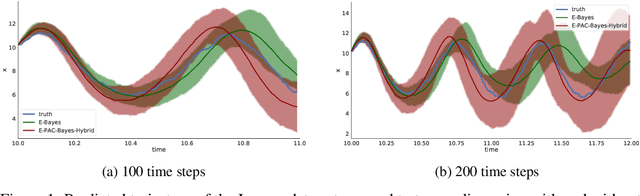
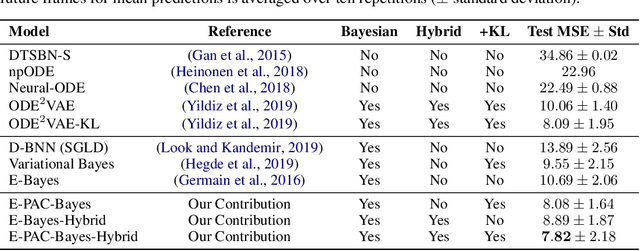
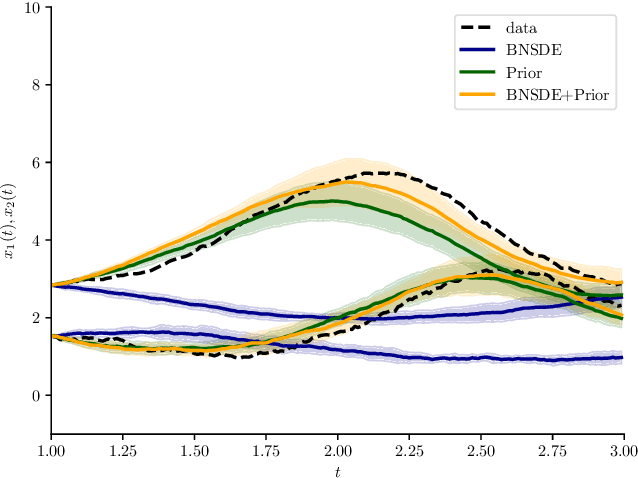
We propose a novel scheme for fitting heavily parameterized non-linear stochastic differential equations (SDEs). We assign a prior on the parameters of the SDE drift and diffusion functions to achieve a Bayesian model. We then infer this model using the well-known local reparameterized trick for the first time for empirical Bayes, i.e. to integrate out the SDE parameters. The model is then fit by maximizing the likelihood of the resultant marginal with respect to a potentially large number of hyperparameters, which prohibits stable training. As the prior parameters are marginalized, the model also no longer provides a principled means to incorporate prior knowledge. We overcome both of these drawbacks by deriving a training loss that comprises the marginal likelihood of the predictor and a PAC-Bayesian complexity penalty. We observe on synthetic as well as real-world time series prediction tasks that our method provides an improved model fit accompanied with favorable extrapolation properties when provided a partial description of the environment dynamics. Hence, we view the outcome as a promising attempt for building cutting-edge hybrid learning systems that effectively combine first-principle physics and data-driven approaches.

Deep Active Learning with Adaptive Acquisition

Model selection is treated as a standard performance boosting step in many machine learning applications. Once all other properties of a learning problem are fixed, the model is selected by grid search on a held-out validation set. This is strictly inapplicable to active learning. Within the standardized workflow, the acquisition function is chosen among available heuristics a priori, and its success is observed only after the labeling budget is already exhausted. More importantly, none of the earlier studies report a unique consistently successful acquisition heuristic to the extent to stand out as the unique best choice. We present a method to break this vicious circle by defining the acquisition function as a learning predictor and training it by reinforcement feedback collected from each labeling round. As active learning is a scarce data regime, we bootstrap from a well-known heuristic that filters the bulk of data points on which all heuristics would agree, and learn a policy to warp the top portion of this ranking in the most beneficial way for the character of a specific data distribution. Our system consists of a Bayesian neural net, the predictor, a bootstrap acquisition function, a probabilistic state definition, and another Bayesian policy network that can effectively incorporate this input distribution. We observe on three benchmark data sets that our method always manages to either invent a new superior acquisition function or to adapt itself to the a priori unknown best performing heuristic for each specific data set.

Bayesian Prior Networks with PAC Training

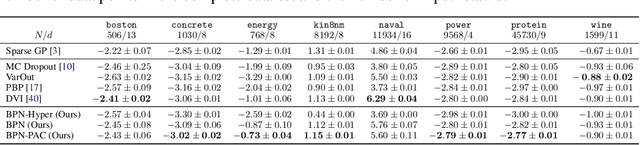
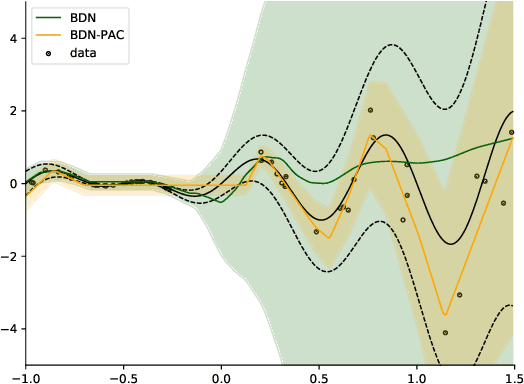
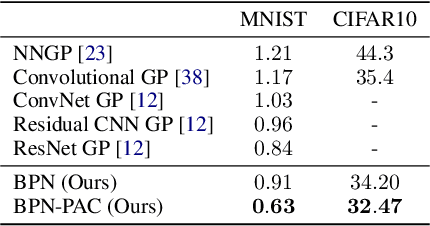
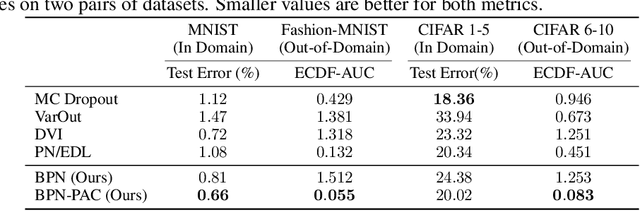
We propose to train Bayesian Neural Networks (BNNs) by empirical Bayes as an alternative to posterior weight inference. By approximately marginalizing out an i.i.d.\ realization of a finite number of sibling weights per data-point using the Central Limit Theorem (CLT), we attain a scalable and effective Bayesian deep predictor. This approach directly models the posterior predictive distribution, by-passing the intractable posterior weight inference step. However, it introduces a prohibitively large number of hyperparameters for stable training. As the prior weights are marginalized and hyperparameters are optimized, the model also no longer provides a means to incorporate prior knowledge. We overcome both of these drawbacks by deriving a trivial PAC bound that comprises the marginal likelihood of the predictor and a complexity penalty. The outcome integrates organically into the prior networks framework, bringing about an effective and holistic Bayesian treatment of prediction uncertainty. We observe on various regression, classification, and out-of-domain detection benchmarks that our scalable method provides an improved model fit accompanied with significantly better uncertainty estimates than the state-of-the-art.

Sampling-Free Variational Inference of Bayesian Neural Nets

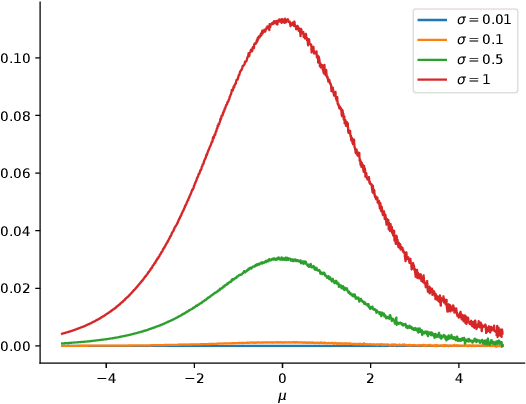
We propose a new Bayesian Neural Net (BNN) formulation that affords variational inference for which the evidence lower bound (ELBO) is analytically tractable subject to a tight approximation. We achieve this tractability by decomposing ReLU nonlinearities into an identity function and a Kronecker delta function. We demonstrate formally that assigning the outputs of these functions to separate latent variables allows representing the neural network likelihood as the composition of a chain of linear operations. Performing variational inference on this construction enables closed-form computation of the evidence lower bound. It can thus be maximized without requiring Monte Carlo sampling to approximate the problematic expected log-likelihood term. The resultant formulation boils down to stochastic gradient descent, where the gradients are not distorted by any factor besides minibatch selection. This amends a long-standing disadvantage of BNNs relative to deterministic nets. Experiments on four benchmark data sets show that the cleaner gradients provided by our construction yield a steeper learning curve, achieving higher prediction accuracies for a fixed epoch budget.