Amortized Safe Active Learning for Real-Time Decision-Making: Pretrained Neural Policies from Simulated Nonparametric Functions

Active Learning (AL) is a sequential learning approach aiming at selecting the most informative data for model training. In many systems, safety constraints appear during data evaluation, requiring the development of safe AL methods. Key challenges of AL are the repeated model training and acquisition optimization required for data selection, which become particularly restrictive under safety constraints. This repeated effort often creates a bottleneck, especially in physical systems requiring real-time decision-making. In this paper, we propose a novel amortized safe AL framework. By leveraging a pretrained neural network policy, our method eliminates the need for repeated model training and acquisition optimization, achieving substantial speed improvements while maintaining competitive learning outcomes and safety awareness. The policy is trained entirely on synthetic data utilizing a novel safe AL objective. The resulting policy is highly versatile and adapts to a wide range of systems, as we demonstrate in our experiments. Furthermore, our framework is modular and we empirically show that we also achieve superior performance for unconstrained time-sensitive AL tasks if we omit the safety requirement.

Amortized Active Learning for Nonparametric Functions

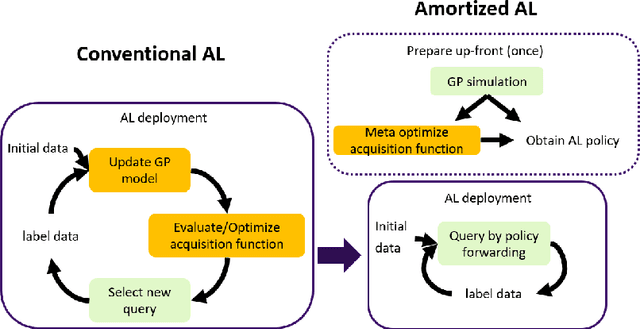
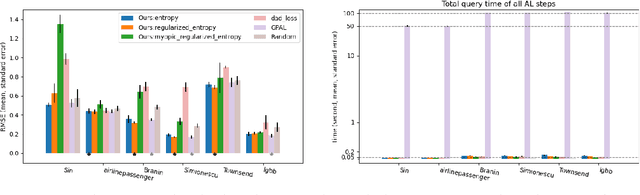
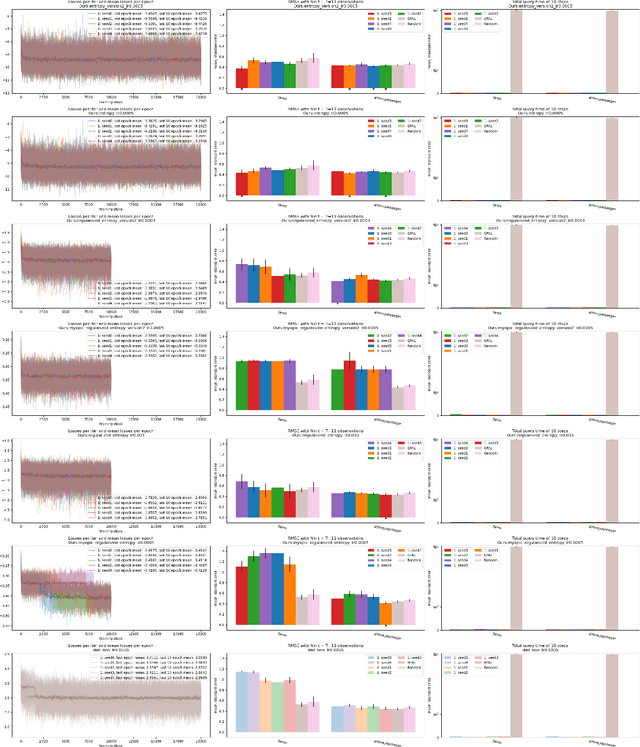
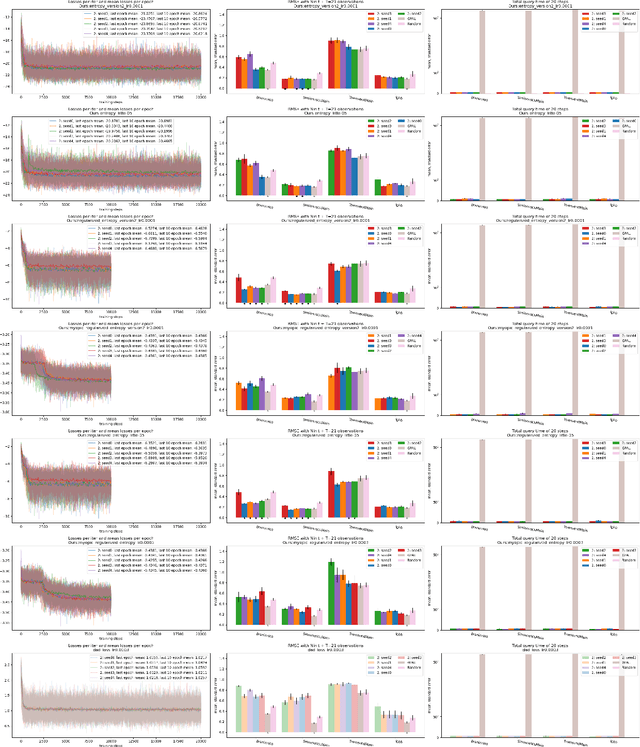
Active learning (AL) is a sequential learning scheme aiming to select the most informative data. AL reduces data consumption and avoids the cost of labeling large amounts of data. However, AL trains the model and solves an acquisition optimization for each selection. It becomes expensive when the model training or acquisition optimization is challenging. In this paper, we focus on active nonparametric function learning, where the gold standard Gaussian process (GP) approaches suffer from cubic time complexity. We propose an amortized AL method, where new data are suggested by a neural network which is trained up-front without any real data (Figure 1). Our method avoids repeated model training and requires no acquisition optimization during the AL deployment. We (i) utilize GPs as function priors to construct an AL simulator, (ii) train an AL policy that can zero-shot generalize from simulation to real learning problems of nonparametric functions and (iii) achieve real-time data selection and comparable learning performances to time-consuming baseline methods.

Global Safe Sequential Learning via Efficient Knowledge Transfer

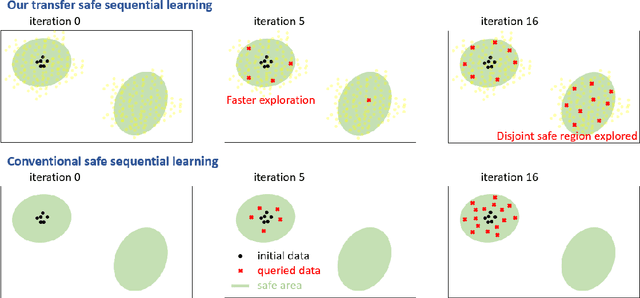
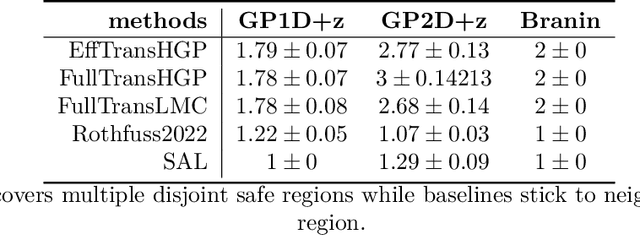
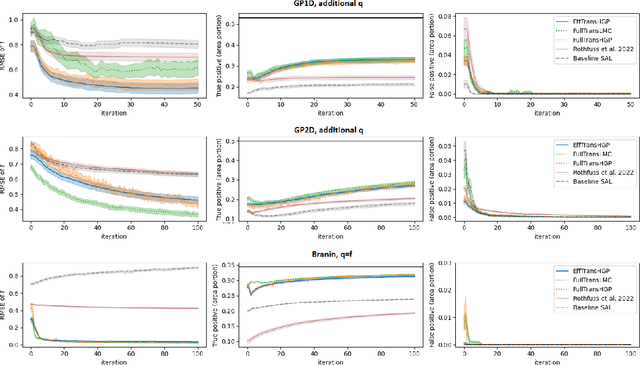
Sequential learning methods such as active learning and Bayesian optimization select the most informative data to learn about a task. In many medical or engineering applications, the data selection is constrained by a priori unknown safety conditions. A promissing line of safe learning methods utilize Gaussian processes (GPs) to model the safety probability and perform data selection in areas with high safety confidence. However, accurate safety modeling requires prior knowledge or consumes data. In addition, the safety confidence centers around the given observations which leads to local exploration. As transferable source knowledge is often available in safety critical experiments, we propose to consider transfer safe sequential learning to accelerate the learning of safety. We further consider a pre-computation of source components to reduce the additional computational load that is introduced by incorporating source data. In this paper, we theoretically analyze the maximum explorable safe regions of conventional safe learning methods. Furthermore, we empirically demonstrate that our approach 1) learns a task with lower data consumption, 2) globally explores multiple disjoint safe regions under guidance of the source knowledge, and 3) operates with computation comparable to conventional safe learning methods.

Hybrid Modeling Design Patterns

Design patterns provide a systematic way to convey solutions to recurring modeling challenges. This paper introduces design patterns for hybrid modeling, an approach that combines modeling based on first principles with data-driven modeling techniques. While both approaches have complementary advantages there are often multiple ways to combine them into a hybrid model, and the appropriate solution will depend on the problem at hand. In this paper, we provide four base patterns that can serve as blueprints for combining data-driven components with domain knowledge into a hybrid approach. In addition, we also present two composition patterns that govern the combination of the base patterns into more complex hybrid models. Each design pattern is illustrated by typical use cases from application areas such as climate modeling, engineering, and physics.

Sampling-Free Probabilistic Deep State-Space Models

Many real-world dynamical systems can be described as State-Space Models (SSMs). In this formulation, each observation is emitted by a latent state, which follows first-order Markovian dynamics. A Probabilistic Deep SSM (ProDSSM) generalizes this framework to dynamical systems of unknown parametric form, where the transition and emission models are described by neural networks with uncertain weights. In this work, we propose the first deterministic inference algorithm for models of this type. Our framework allows efficient approximations for training and testing. We demonstrate in our experiments that our new method can be employed for a variety of tasks and enjoys a superior balance between predictive performance and computational budget.

Can you text what is happening? Integrating pre-trained language encoders into trajectory prediction models for autonomous driving

In autonomous driving tasks, scene understanding is the first step towards predicting the future behavior of the surrounding traffic participants. Yet, how to represent a given scene and extract its features are still open research questions. In this study, we propose a novel text-based representation of traffic scenes and process it with a pre-trained language encoder. First, we show that text-based representations, combined with classical rasterized image representations, lead to descriptive scene embeddings. Second, we benchmark our predictions on the nuScenes dataset and show significant improvements compared to baselines. Third, we show in an ablation study that a joint encoder of text and rasterized images outperforms the individual encoders confirming that both representations have their complementary strengths.

Cheap and Deterministic Inference for Deep State-Space Models of Interacting Dynamical Systems

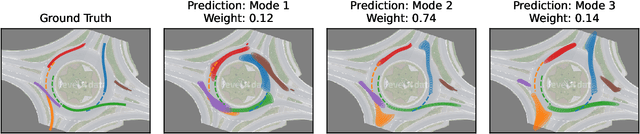
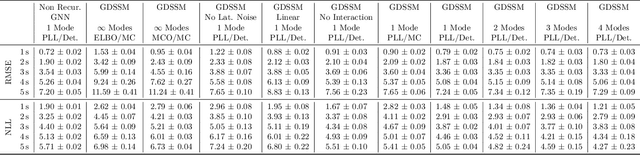
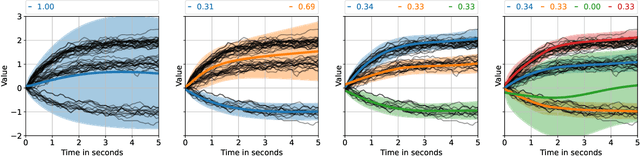
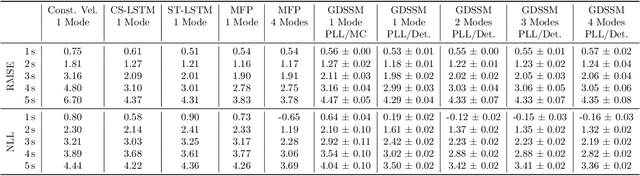
Graph neural networks are often used to model interacting dynamical systems since they gracefully scale to systems with a varying and high number of agents. While there has been much progress made for deterministic interacting systems, modeling is much more challenging for stochastic systems in which one is interested in obtaining a predictive distribution over future trajectories. Existing methods are either computationally slow since they rely on Monte Carlo sampling or make simplifying assumptions such that the predictive distribution is unimodal. In this work, we present a deep state-space model which employs graph neural networks in order to model the underlying interacting dynamical system. The predictive distribution is multimodal and has the form of a Gaussian mixture model, where the moments of the Gaussian components can be computed via deterministic moment matching rules. Our moment matching scheme can be exploited for sample-free inference, leading to more efficient and stable training compared to Monte Carlo alternatives. Furthermore, we propose structured approximations to the covariance matrices of the Gaussian components in order to scale up to systems with many agents. We benchmark our novel framework on two challenging autonomous driving datasets. Both confirm the benefits of our method compared to state-of-the-art methods. We further demonstrate the usefulness of our individual contributions in a carefully designed ablation study and provide a detailed runtime analysis of our proposed covariance approximations. Finally, we empirically demonstrate the generalization ability of our method by evaluating its performance on unseen scenarios.

Combining Slow and Fast: Complementary Filtering for Dynamics Learning

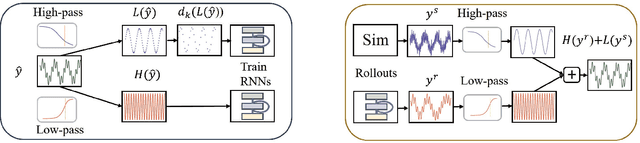
Modeling an unknown dynamical system is crucial in order to predict the future behavior of the system. A standard approach is training recurrent models on measurement data. While these models typically provide exact short-term predictions, accumulating errors yield deteriorated long-term behavior. In contrast, models with reliable long-term predictions can often be obtained, either by training a robust but less detailed model, or by leveraging physics-based simulations. In both cases, inaccuracies in the models yield a lack of short-time details. Thus, different models with contrastive properties on different time horizons are available. This observation immediately raises the question: Can we obtain predictions that combine the best of both worlds? Inspired by sensor fusion tasks, we interpret the problem in the frequency domain and leverage classical methods from signal processing, in particular complementary filters. This filtering technique combines two signals by applying a high-pass filter to one signal, and low-pass filtering the other. Essentially, the high-pass filter extracts high-frequencies, whereas the low-pass filter extracts low frequencies. Applying this concept to dynamics model learning enables the construction of models that yield accurate long- and short-term predictions. Here, we propose two methods, one being purely learning-based and the other one being a hybrid model that requires an additional physics-based simulator.

Learning Interacting Dynamical Systems with Latent Gaussian Process ODEs

We study for the first time uncertainty-aware modeling of continuous-time dynamics of interacting objects. We introduce a new model that decomposes independent dynamics of single objects accurately from their interactions. By employing latent Gaussian process ordinary differential equations, our model infers both independent dynamics and their interactions with reliable uncertainty estimates. In our formulation, each object is represented as a graph node and interactions are modeled by accumulating the messages coming from neighboring objects. We show that efficient inference of such a complex network of variables is possible with modern variational sparse Gaussian process inference techniques. We empirically demonstrate that our model improves the reliability of long-term predictions over neural network based alternatives and it successfully handles missing dynamic or static information. Furthermore, we observe that only our model can successfully encapsulate independent dynamics and interaction information in distinct functions and show the benefit from this disentanglement in extrapolation scenarios.

Safe Active Learning for Multi-Output Gaussian Processes

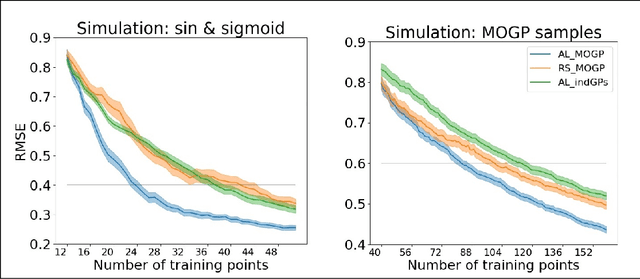
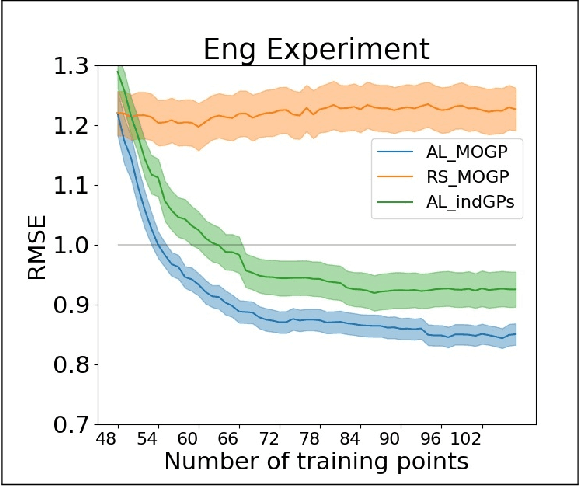
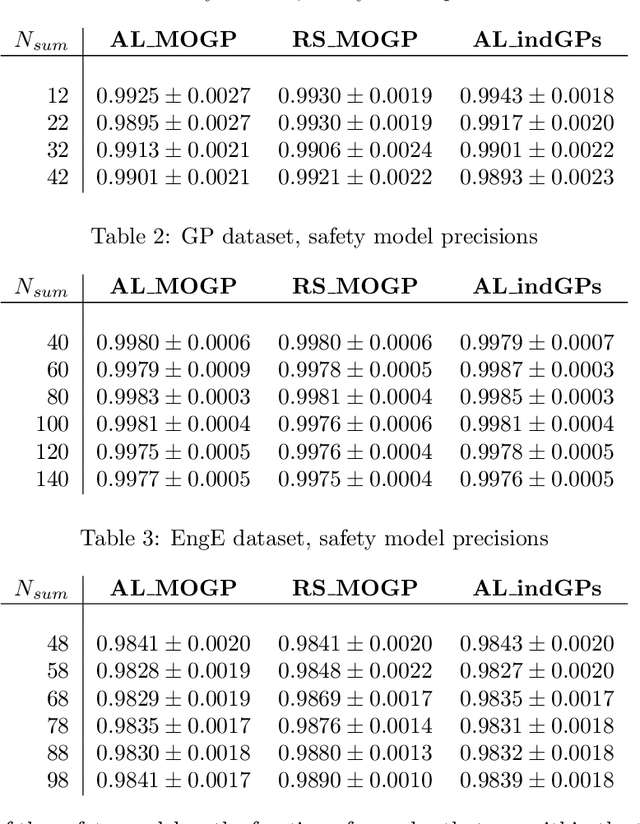
Multi-output regression problems are commonly encountered in science and engineering. In particular, multi-output Gaussian processes have been emerged as a promising tool for modeling these complex systems since they can exploit the inherent correlations and provide reliable uncertainty estimates. In many applications, however, acquiring the data is expensive and safety concerns might arise (e.g. robotics, engineering). We propose a safe active learning approach for multi-output Gaussian process regression. This approach queries the most informative data or output taking the relatedness between the regressors and safety constraints into account. We prove the effectiveness of our approach by providing theoretical analysis and by demonstrating empirical results on simulated datasets and on a real-world engineering dataset. On all datasets, our approach shows improved convergence compared to its competitors.