Analyzing Closed-loop Training Techniques for Realistic Traffic Agent Models in Autonomous Highway Driving Simulations

Simulation plays a crucial role in the rapid development and safe deployment of autonomous vehicles. Realistic traffic agent models are indispensable for bridging the gap between simulation and the real world. Many existing approaches for imitating human behavior are based on learning from demonstration. However, these approaches are often constrained by focusing on individual training strategies. Therefore, to foster a broader understanding of realistic traffic agent modeling, in this paper, we provide an extensive comparative analysis of different training principles, with a focus on closed-loop methods for highway driving simulation. We experimentally compare (i) open-loop vs. closed-loop multi-agent training, (ii) adversarial vs. deterministic supervised training, (iii) the impact of reinforcement losses, and (iv) the impact of training alongside log-replayed agents to identify suitable training techniques for realistic agent modeling. Furthermore, we identify promising combinations of different closed-loop training methods.

Learning Hybrid Dynamics Models With Simulator-Informed Latent States

Dynamics model learning deals with the task of inferring unknown dynamics from measurement data and predicting the future behavior of the system. A typical approach to address this problem is to train recurrent models. However, predictions with these models are often not physically meaningful. Further, they suffer from deteriorated behavior over time due to accumulating errors. Often, simulators building on first principles are available being physically meaningful by design. However, modeling simplifications typically cause inaccuracies in these models. Consequently, hybrid modeling is an emerging trend that aims to combine the best of both worlds. In this paper, we propose a new approach to hybrid modeling, where we inform the latent states of a learned model via a black-box simulator. This allows to control the predictions via the simulator preventing them from accumulating errors. This is especially challenging since, in contrast to previous approaches, access to the simulator's latent states is not available. We tackle the task by leveraging observers, a well-known concept from control theory, inferring unknown latent states from observations and dynamics over time. In our learning-based setting, we jointly learn the dynamics and an observer that infers the latent states via the simulator. Thus, the simulator constantly corrects the latent states, compensating for modeling mismatch caused by learning. To maintain flexibility, we train an RNN-based residuum for the latent states that cannot be informed by the simulator.

Exact Inference for Continuous-Time Gaussian Process Dynamics

Physical systems can often be described via a continuous-time dynamical system. In practice, the true system is often unknown and has to be learned from measurement data. Since data is typically collected in discrete time, e.g. by sensors, most methods in Gaussian process (GP) dynamics model learning are trained on one-step ahead predictions. This can become problematic in several scenarios, e.g. if measurements are provided at irregularly-sampled time steps or physical system properties have to be conserved. Thus, we aim for a GP model of the true continuous-time dynamics. Higher-order numerical integrators provide the necessary tools to address this problem by discretizing the dynamics function with arbitrary accuracy. Many higher-order integrators require dynamics evaluations at intermediate time steps making exact GP inference intractable. In previous work, this problem is often tackled by approximating the GP posterior with variational inference. However, exact GP inference is preferable in many scenarios, e.g. due to its mathematical guarantees. In order to make direct inference tractable, we propose to leverage multistep and Taylor integrators. We demonstrate how to derive flexible inference schemes for these types of integrators. Further, we derive tailored sampling schemes that allow to draw consistent dynamics functions from the learned posterior. This is crucial to sample consistent predictions from the dynamics model. We demonstrate empirically and theoretically that our approach yields an accurate representation of the continuous-time system.

Combining Slow and Fast: Complementary Filtering for Dynamics Learning

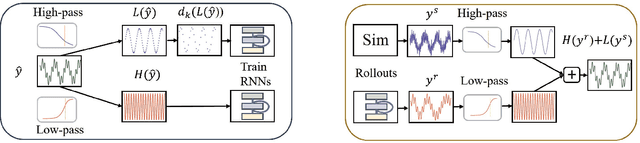
Modeling an unknown dynamical system is crucial in order to predict the future behavior of the system. A standard approach is training recurrent models on measurement data. While these models typically provide exact short-term predictions, accumulating errors yield deteriorated long-term behavior. In contrast, models with reliable long-term predictions can often be obtained, either by training a robust but less detailed model, or by leveraging physics-based simulations. In both cases, inaccuracies in the models yield a lack of short-time details. Thus, different models with contrastive properties on different time horizons are available. This observation immediately raises the question: Can we obtain predictions that combine the best of both worlds? Inspired by sensor fusion tasks, we interpret the problem in the frequency domain and leverage classical methods from signal processing, in particular complementary filters. This filtering technique combines two signals by applying a high-pass filter to one signal, and low-pass filtering the other. Essentially, the high-pass filter extracts high-frequencies, whereas the low-pass filter extracts low frequencies. Applying this concept to dynamics model learning enables the construction of models that yield accurate long- and short-term predictions. Here, we propose two methods, one being purely learning-based and the other one being a hybrid model that requires an additional physics-based simulator.

Wasserstein Adversarial Imitation Learning

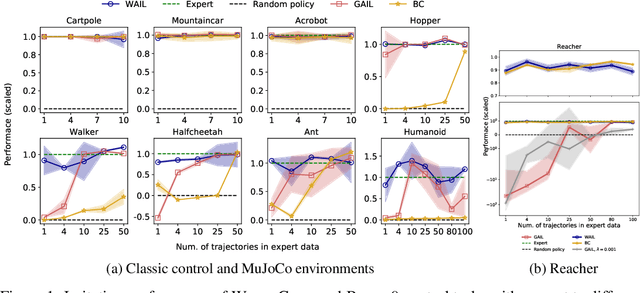
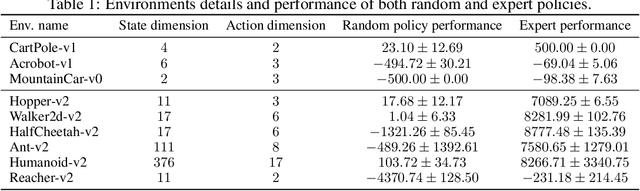
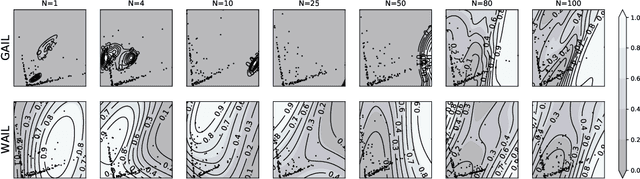
Imitation Learning describes the problem of recovering an expert policy from demonstrations. While inverse reinforcement learning approaches are known to be very sample-efficient in terms of expert demonstrations, they usually require problem-dependent reward functions or a (task-)specific reward-function regularization. In this paper, we show a natural connection between inverse reinforcement learning approaches and Optimal Transport, that enables more general reward functions with desirable properties (e.g., smoothness). Based on our observation, we propose a novel approach called Wasserstein Adversarial Imitation Learning. Our approach considers the Kantorovich potentials as a reward function and further leverages regularized optimal transport to enable large-scale applications. In several robotic experiments, our approach outperforms the baselines in terms of average cumulative rewards and shows a significant improvement in sample-efficiency, by requiring just one expert demonstration.