Wasserstein Adversarial Imitation Learning
Paper and Code
Jun 19, 2019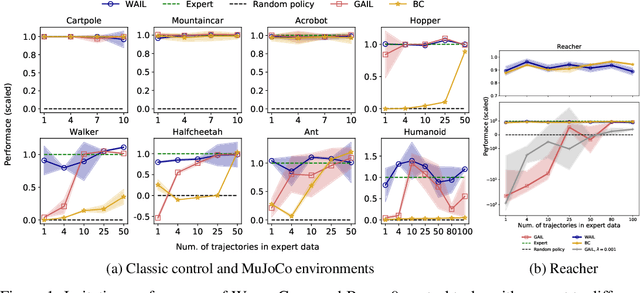
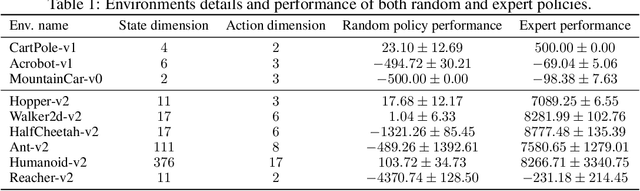
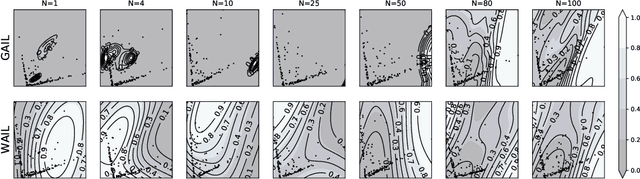
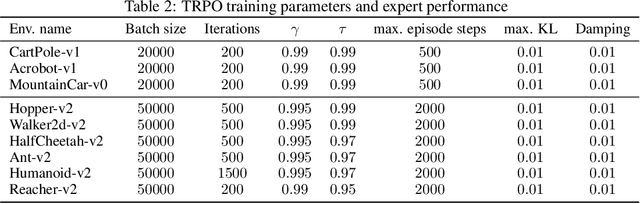
Imitation Learning describes the problem of recovering an expert policy from demonstrations. While inverse reinforcement learning approaches are known to be very sample-efficient in terms of expert demonstrations, they usually require problem-dependent reward functions or a (task-)specific reward-function regularization. In this paper, we show a natural connection between inverse reinforcement learning approaches and Optimal Transport, that enables more general reward functions with desirable properties (e.g., smoothness). Based on our observation, we propose a novel approach called Wasserstein Adversarial Imitation Learning. Our approach considers the Kantorovich potentials as a reward function and further leverages regularized optimal transport to enable large-scale applications. In several robotic experiments, our approach outperforms the baselines in terms of average cumulative rewards and shows a significant improvement in sample-efficiency, by requiring just one expert demonstration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge