Recommendations from Sparse Comparison Data: Provably Fast Convergence for Nonconvex Matrix Factorization

This paper provides a theoretical analysis of a new learning problem for recommender systems where users provide feedback by comparing pairs of items instead of rating them individually. We assume that comparisons stem from latent user and item features, which reduces the task of predicting preferences to learning these features from comparison data. Similar to the classical matrix factorization problem, the main challenge in this learning task is that the resulting loss function is nonconvex. Our analysis shows that the loss function exhibits (restricted) strong convexity near the true solution, which ensures gradient-based methods converge exponentially, given an appropriate warm start. Importantly, this result holds in a sparse data regime, where each user compares only a few pairs of items. Our main technical contribution is to extend certain concentration inequalities commonly used in matrix completion to our model. Our work demonstrates that learning personalized recommendations from comparison data is computationally and statistically efficient.

Riemannian Manifold Learning for Stackelberg Games with Neural Flow Representations

We present a novel framework for online learning in Stackelberg general-sum games, where two agents, the leader and follower, engage in sequential turn-based interactions. At the core of this approach is a learned diffeomorphism that maps the joint action space to a smooth Riemannian manifold, referred to as the Stackelberg manifold. This mapping, facilitated by neural normalizing flows, ensures the formation of tractable isoplanar subspaces, enabling efficient techniques for online learning. By assuming linearity between the agents' reward functions on the Stackelberg manifold, our construct allows the application of standard bandit algorithms. We then provide a rigorous theoretical basis for regret minimization on convex manifolds and establish finite-time bounds on simple regret for learning Stackelberg equilibria. This integration of manifold learning into game theory uncovers a previously unrecognized potential for neural normalizing flows as an effective tool for multi-agent learning. We present empirical results demonstrating the effectiveness of our approach compared to standard baselines, with applications spanning domains such as cybersecurity and economic supply chain optimization.

Fast Proxy Experiment Design for Causal Effect Identification

Identifying causal effects is a key problem of interest across many disciplines. The two long-standing approaches to estimate causal effects are observational and experimental (randomized) studies. Observational studies can suffer from unmeasured confounding, which may render the causal effects unidentifiable. On the other hand, direct experiments on the target variable may be too costly or even infeasible to conduct. A middle ground between these two approaches is to estimate the causal effect of interest through proxy experiments, which are conducted on variables with a lower cost to intervene on compared to the main target. Akbari et al. [2022] studied this setting and demonstrated that the problem of designing the optimal (minimum-cost) experiment for causal effect identification is NP-complete and provided a naive algorithm that may require solving exponentially many NP-hard problems as a sub-routine in the worst case. In this work, we provide a few reformulations of the problem that allow for designing significantly more efficient algorithms to solve it as witnessed by our extensive simulations. Additionally, we study the closely-related problem of designing experiments that enable us to identify a given effect through valid adjustments sets.

Parameter identification in linear non-Gaussian causal models under general confounding

Linear non-Gaussian causal models postulate that each random variable is a linear function of parent variables and non-Gaussian exogenous error terms. We study identification of the linear coefficients when such models contain latent variables. Our focus is on the commonly studied acyclic setting, where each model corresponds to a directed acyclic graph (DAG). For this case, prior literature has demonstrated that connections to overcomplete independent component analysis yield effective criteria to decide parameter identifiability in latent variable models. However, this connection is based on the assumption that the observed variables linearly depend on the latent variables. Departing from this assumption, we treat models that allow for arbitrary non-linear latent confounding. Our main result is a graphical criterion that is necessary and sufficient for deciding the generic identifiability of direct causal effects. Moreover, we provide an algorithmic implementation of the criterion with a run time that is polynomial in the number of observed variables. Finally, we report on estimation heuristics based on the identification result, explore a generalization to models with feedback loops, and provide new results on the identifiability of the causal graph.

Confounded Budgeted Causal Bandits

We study the problem of learning 'good' interventions in a stochastic environment modeled by its underlying causal graph. Good interventions refer to interventions that maximize rewards. Specifically, we consider the setting of a pre-specified budget constraint, where interventions can have non-uniform costs. We show that this problem can be formulated as maximizing the expected reward for a stochastic multi-armed bandit with side information. We propose an algorithm to minimize the cumulative regret in general causal graphs. This algorithm trades off observations and interventions based on their costs to achieve the optimal reward. This algorithm generalizes the state-of-the-art methods by allowing non-uniform costs and hidden confounders in the causal graph. Furthermore, we develop an algorithm to minimize the simple regret in the budgeted setting with non-uniform costs and also general causal graphs. We provide theoretical guarantees, including both upper and lower bounds, as well as empirical evaluations of our algorithms. Our empirical results showcase that our algorithms outperform the state of the art.

Modeling Systemic Risk: A Time-Varying Nonparametric Causal Inference Framework

We propose a nonparametric and time-varying directed information graph (TV-DIG) framework to estimate the evolving causal structure in time series networks, thereby addressing the limitations of traditional econometric models in capturing high-dimensional, nonlinear, and time-varying interconnections among series. This framework employs an information-theoretic measure rooted in a generalized version of Granger-causality, which is applicable to both linear and nonlinear dynamics. Our framework offers advancements in measuring systemic risk and establishes meaningful connections with established econometric models, including vector autoregression and switching models. We evaluate the efficacy of our proposed model through simulation experiments and empirical analysis, reporting promising results in recovering simulated time-varying networks with nonlinear and multivariate structures. We apply this framework to identify and monitor the evolution of interconnectedness and systemic risk among major assets and industrial sectors within the financial network. We focus on cryptocurrencies' potential systemic risks to financial stability, including spillover effects on other sectors during crises like the COVID-19 pandemic and the Federal Reserve's 2020 emergency response. Our findings reveals significant, previously underrecognized pre-2020 influences of cryptocurrencies on certain financial sectors, highlighting their potential systemic risks and offering a systematic approach in tracking evolving cross-sector interactions within financial networks.

On Identifiability of Conditional Causal Effects

We address the problem of identifiability of an arbitrary conditional causal effect given both the causal graph and a set of any observational and/or interventional distributions of the form $Q[S]:=P(S|do(V\setminus S))$, where $V$ denotes the set of all observed variables and $S\subseteq V$. We call this problem conditional generalized identifiability (c-gID in short) and prove the completeness of Pearl's $do$-calculus for the c-gID problem by providing sound and complete algorithm for the c-gID problem. This work revisited the c-gID problem in Lee et al. [2020], Correa et al. [2021] by adding explicitly the positivity assumption which is crucial for identifiability. It extends the results of [Lee et al., 2019, Kivva et al., 2022] on general identifiability (gID) which studied the problem for unconditional causal effects and Shpitser and Pearl [2006b] on identifiability of conditional causal effects given merely the observational distribution $P(\mathbf{V})$ as our algorithm generalizes the algorithms proposed in [Kivva et al., 2022] and [Shpitser and Pearl, 2006b].

Causal Bandits without Graph Learning

We study the causal bandit problem when the causal graph is unknown and develop an efficient algorithm for finding the parent node of the reward node using atomic interventions. We derive the exact equation for the expected number of interventions performed by the algorithm and show that under certain graphical conditions it could perform either logarithmically fast or, under more general assumptions, slower but still sublinearly in the number of variables. We formally show that our algorithm is optimal as it meets the universal lower bound we establish for any algorithm that performs atomic interventions. Finally, we extend our algorithm to the case when the reward node has multiple parents. Using this algorithm together with a standard algorithm from bandit literature leads to improved regret bounds.

Novel Ordering-based Approaches for Causal Structure Learning in the Presence of Unobserved Variables

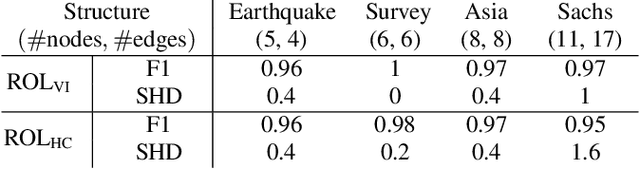
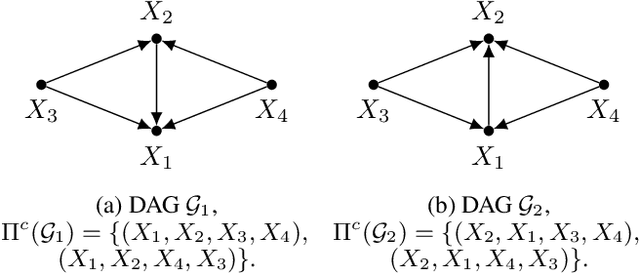
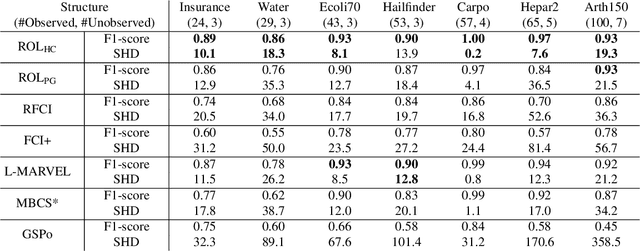
We propose ordering-based approaches for learning the maximal ancestral graph (MAG) of a structural equation model (SEM) up to its Markov equivalence class (MEC) in the presence of unobserved variables. Existing ordering-based methods in the literature recover a graph through learning a causal order (c-order). We advocate for a novel order called removable order (r-order) as they are advantageous over c-orders for structure learning. This is because r-orders are the minimizers of an appropriately defined optimization problem that could be either solved exactly (using a reinforcement learning approach) or approximately (using a hill-climbing search). Moreover, the r-orders (unlike c-orders) are invariant among all the graphs in a MEC and include c-orders as a subset. Given that set of r-orders is often significantly larger than the set of c-orders, it is easier for the optimization problem to find an r-order instead of a c-order. We evaluate the performance and the scalability of our proposed approaches on both real-world and randomly generated networks.

Causal Discovery in Probabilistic Networks with an Identifiable Causal Effect

Causal identification is at the core of the causal inference literature, where complete algorithms have been proposed to identify causal queries of interest. The validity of these algorithms hinges on the restrictive assumption of having access to a correctly specified causal structure. In this work, we study the setting where a probabilistic model of the causal structure is available. Specifically, the edges in a causal graph are assigned probabilities which may, for example, represent degree of belief from domain experts. Alternatively, the uncertainly about an edge may reflect the confidence of a particular statistical test. The question that naturally arises in this setting is: Given such a probabilistic graph and a specific causal effect of interest, what is the subgraph which has the highest plausibility and for which the causal effect is identifiable? We show that answering this question reduces to solving an NP-hard combinatorial optimization problem which we call the edge ID problem. We propose efficient algorithms to approximate this problem, and evaluate our proposed algorithms against real-world networks and randomly generated graphs.