Monte Carlo Planning for Stochastic Control on Constrained Markov Decision Processes

In the world of stochastic control, especially in economics and engineering, Markov Decision Processes (MDPs) can effectively model various stochastic decision processes, from asset management to transportation optimization. These underlying MDPs, upon closer examination, often reveal a specifically constrained causal structure concerning the transition and reward dynamics. By exploiting this structure, we can obtain a reduction in the causal representation of the problem setting, allowing us to solve of the optimal value function more efficiently. This work defines an MDP framework, the \texttt{SD-MDP}, where we disentangle the causal structure of MDPs' transition and reward dynamics, providing distinct partitions on the temporal causal graph. With this stochastic reduction, the \texttt{SD-MDP} reflects a general class of resource allocation problems. This disentanglement further enables us to derive theoretical guarantees on the estimation error of the value function under an optimal policy by allowing independent value estimation from Monte Carlo sampling. Subsequently, by integrating this estimator into well-known Monte Carlo planning algorithms, such as Monte Carlo Tree Search (MCTS), we derive bounds on the simple regret of the algorithm. Finally, we quantify the policy improvement of MCTS under the \texttt{SD-MDP} framework by demonstrating that the MCTS planning algorithm achieves higher expected reward (lower costs) under a constant simulation budget, on a tangible economic example based on maritime refuelling.

Approximate Nash Equilibrium Learning for n-Player Markov Games in Dynamic Pricing

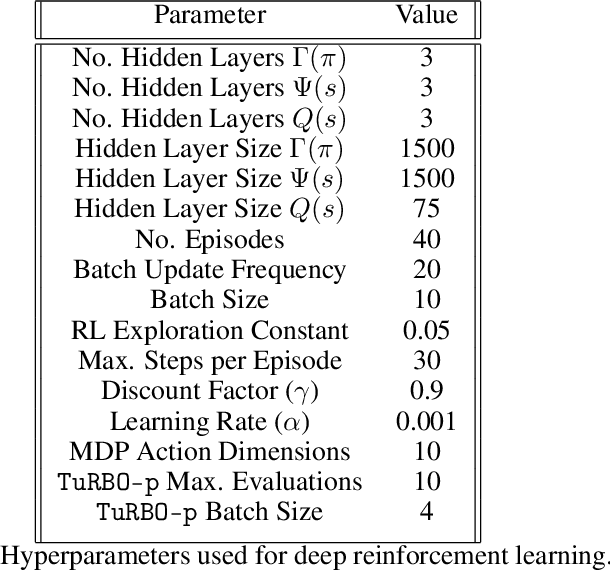
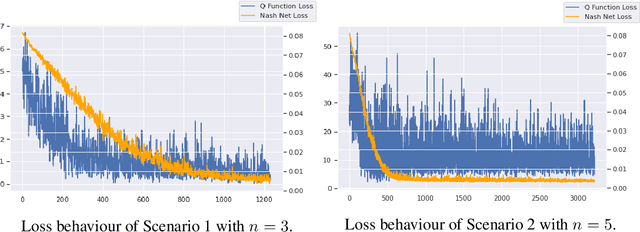
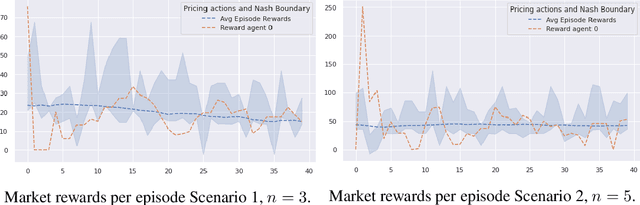
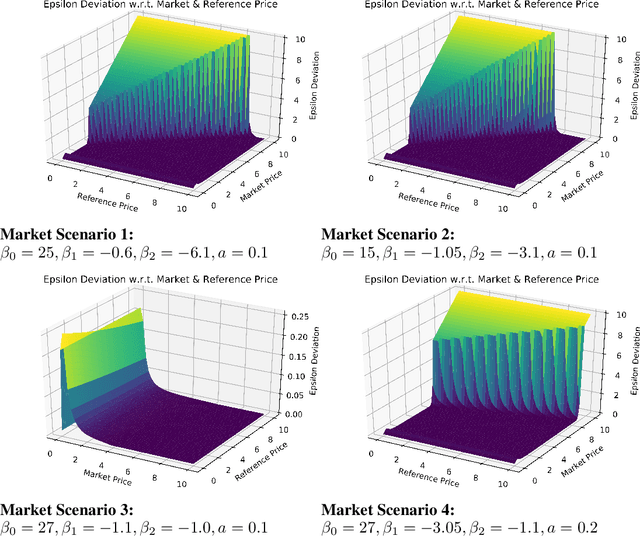
We investigate Nash equilibrium learning in a competitive Markov Game (MG) environment, where multiple agents compete, and multiple Nash equilibria can exist. In particular, for an oligopolistic dynamic pricing environment, exact Nash equilibria are difficult to obtain due to the curse-of-dimensionality. We develop a new model-free method to find approximate Nash equilibria. Gradient-free black box optimization is then applied to estimate $\epsilon$, the maximum reward advantage of an agent unilaterally deviating from any joint policy, and to also estimate the $\epsilon$-minimizing policy for any given state. The policy-$\epsilon$ correspondence and the state to $\epsilon$-minimizing policy are represented by neural networks, the latter being the Nash Policy Net. During batch update, we perform Nash Q learning on the system, by adjusting the action probabilities using the Nash Policy Net. We demonstrate that an approximate Nash equilibrium can be learned, particularly in the dynamic pricing domain where exact solutions are often intractable.

An Extensible and Modular Design and Implementation of Monte Carlo Tree Search for the JVM

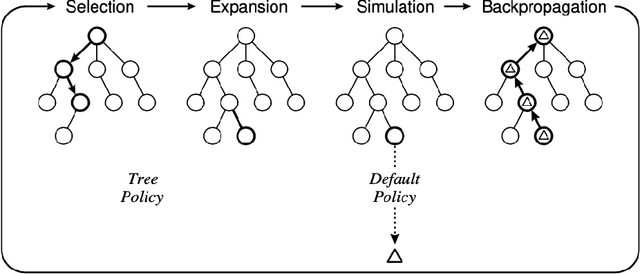
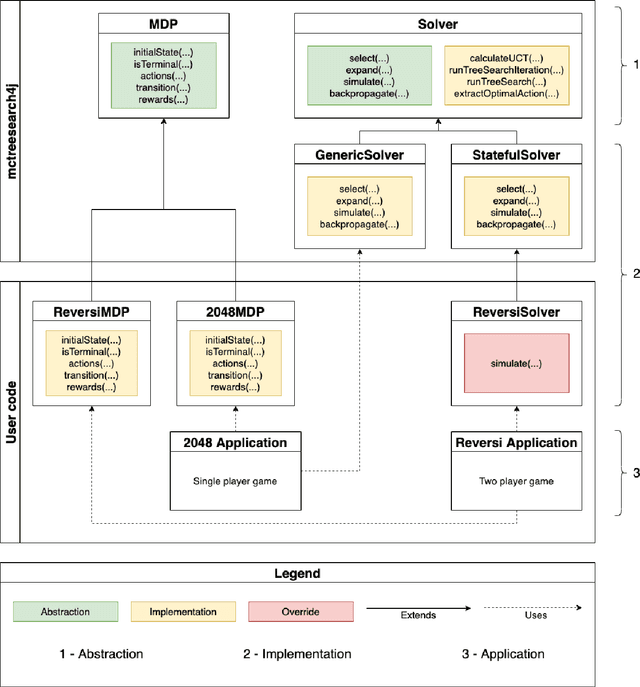
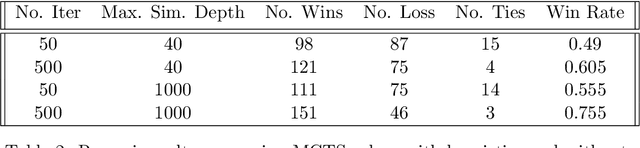
Flexible implementations of Monte Carlo Tree Search (MCTS), combined with domain specific knowledge and hybridization with other search algorithms, can be powerful for finding the solutions to problems in complex planning. We introduce mctreesearch4j, an MCTS implementation written as a standard JVM library following key design principles of object oriented programming. We define key class abstractions allowing the MCTS library to flexibly adapt to any well defined Markov Decision Process or turn-based adversarial game. Furthermore, our library is designed to be modular and extensible, utilizing class inheritance and generic typing to standardize custom algorithm definitions. We demonstrate that the design of the MCTS implementation provides ease of adaptation for unique heuristics and customization across varying Markov Decision Process (MDP) domains. In addition, the implementation is reasonably performant and accurate for standard MDP's. In addition, via the implementation of mctreesearch4j, the nuances of different types of MCTS algorithms are discussed.

Improving the Performance of the LSTM and HMM Models via Hybridization

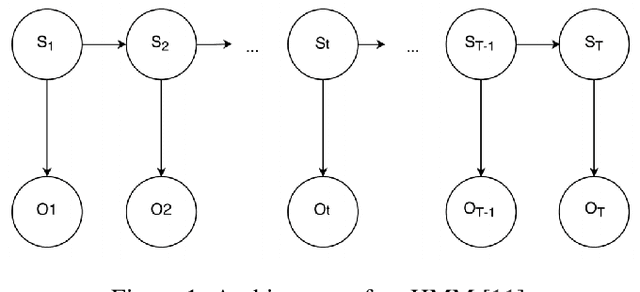
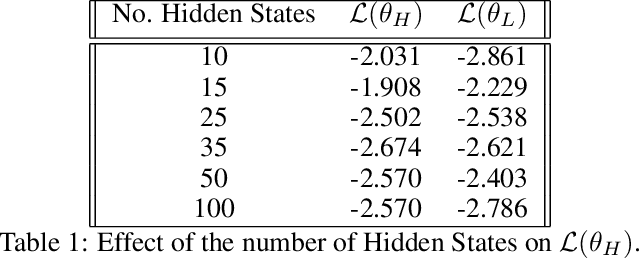
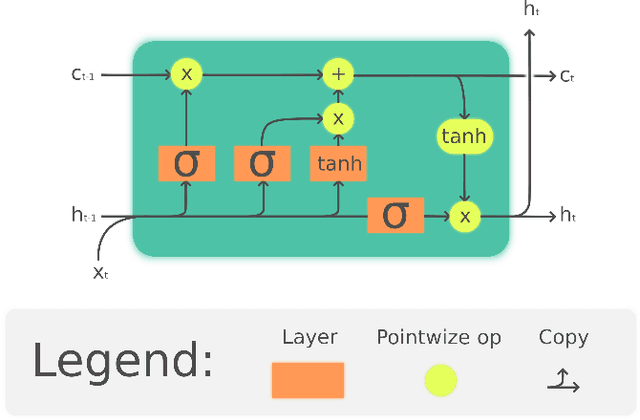
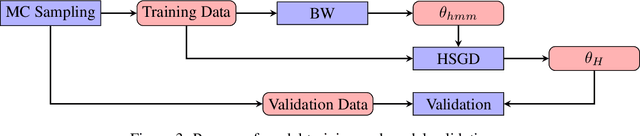
Language models based on deep neural neural networks and traditionalstochastic modelling has become both highly functional and effective in recenttimes. In this work a general survey into the two types of language modelling is conducted. We investigate the effectiveness of a combination of the Hidden Markov Model (HMM) with the Long Short-Term Memory (LSTM) model via a process known as hybridization, which we introduce in this paper. This process involves combining the substitution of hidden state probabilities of the HMM into those of the LSTM. We conduct Monte Carlo sampling to produce training and validation of the data in order to produce robust results. The experimental results of this work displayed an increase in the predictive accuracy of LSTM model when hybridized with the HMM.

Multi-Armed Bandit Strategies for Non-Stationary Reward Distributions and Delayed Feedback Processes

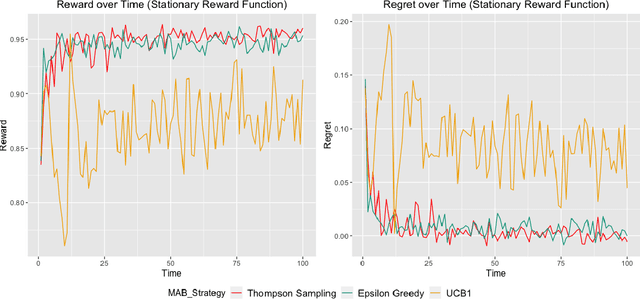
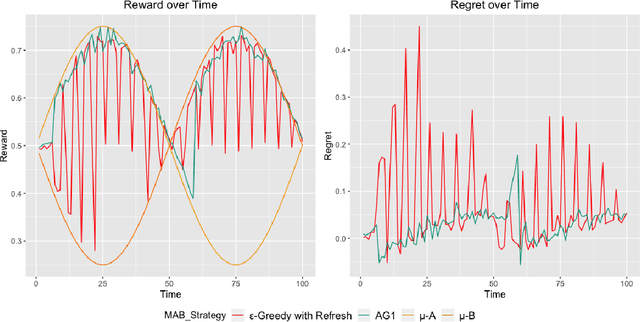
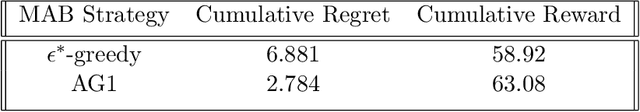
A survey is performed of various Multi-Armed Bandit (MAB) strategies in order to examine their performance in circumstances exhibiting non-stationary stochastic reward functions in conjunction with delayed feedback. We run several MAB simulations to simulate an online eCommerce platform for grocery pick up, optimizing for product availability. In this work, we evaluate several popular MAB strategies, such as $\epsilon$-greedy, UCB1, and Thompson Sampling. We compare the respective performances of each MAB strategy in the context of regret minimization. We run the analysis in the scenario where the reward function is non-stationary. Furthermore, the process experiences delayed feedback, where the reward function is not immediately responsive to the arm played. We devise a new Bayesian technique (BAG1) tailored for non-stationary reward functions in the delayed feedback scenario. The results of the simulation show show superior performance in the context of regret minimization compared to traditional MAB strategies.