Mean-Field Bayesian Optimisation

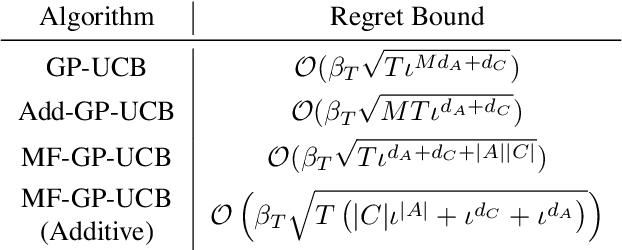
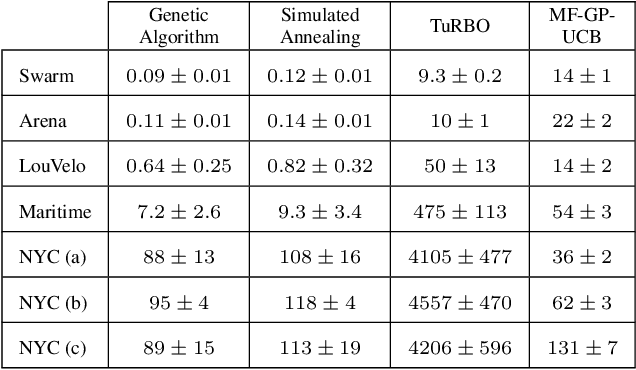
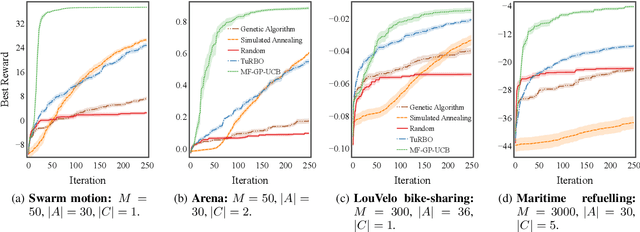
We address the problem of optimising the average payoff for a large number of cooperating agents, where the payoff function is unknown and treated as a black box. While standard Bayesian Optimisation (BO) methods struggle with the scalability required for high-dimensional input spaces, we demonstrate how leveraging the mean-field assumption on the black-box function can transform BO into an efficient and scalable solution. Specifically, we introduce MF-GP-UCB, a novel efficient algorithm designed to optimise agent payoffs in this setting. Our theoretical analysis establishes a regret bound for MF-GP-UCB that is independent of the number of agents, contrasting sharply with the exponential dependence observed when naive BO methods are applied. We evaluate our algorithm on a diverse set of tasks, including real-world problems, such as optimising the location of public bikes for a bike-sharing programme, distributing taxi fleets, and selecting refuelling ports for maritime vessels. Empirical results demonstrate that MF-GP-UCB significantly outperforms existing benchmarks, offering substantial improvements in performance and scalability, constituting a promising solution for mean-field, black-box optimisation. The code is available at https://github.com/petarsteinberg/MF-BO.

Monte Carlo Planning for Stochastic Control on Constrained Markov Decision Processes

In the world of stochastic control, especially in economics and engineering, Markov Decision Processes (MDPs) can effectively model various stochastic decision processes, from asset management to transportation optimization. These underlying MDPs, upon closer examination, often reveal a specifically constrained causal structure concerning the transition and reward dynamics. By exploiting this structure, we can obtain a reduction in the causal representation of the problem setting, allowing us to solve of the optimal value function more efficiently. This work defines an MDP framework, the \texttt{SD-MDP}, where we disentangle the causal structure of MDPs' transition and reward dynamics, providing distinct partitions on the temporal causal graph. With this stochastic reduction, the \texttt{SD-MDP} reflects a general class of resource allocation problems. This disentanglement further enables us to derive theoretical guarantees on the estimation error of the value function under an optimal policy by allowing independent value estimation from Monte Carlo sampling. Subsequently, by integrating this estimator into well-known Monte Carlo planning algorithms, such as Monte Carlo Tree Search (MCTS), we derive bounds on the simple regret of the algorithm. Finally, we quantify the policy improvement of MCTS under the \texttt{SD-MDP} framework by demonstrating that the MCTS planning algorithm achieves higher expected reward (lower costs) under a constant simulation budget, on a tangible economic example based on maritime refuelling.

Safe Model-Based Multi-Agent Mean-Field Reinforcement Learning

Many applications, e.g., in shared mobility, require coordinating a large number of agents. Mean-field reinforcement learning addresses the resulting scalability challenge by optimizing the policy of a representative agent. In this paper, we address an important generalization where there exist global constraints on the distribution of agents (e.g., requiring capacity constraints or minimum coverage requirements to be met). We propose Safe-$\text{M}^3$-UCRL, the first model-based algorithm that attains safe policies even in the case of unknown transition dynamics. As a key ingredient, it uses epistemic uncertainty in the transition model within a log-barrier approach to ensure pessimistic constraints satisfaction with high probability. We showcase Safe-$\text{M}^3$-UCRL on the vehicle repositioning problem faced by many shared mobility operators and evaluate its performance through simulations built on Shenzhen taxi trajectory data. Our algorithm effectively meets the demand in critical areas while ensuring service accessibility in regions with low demand.

Efficient Planning in Combinatorial Action Spaces with Applications to Cooperative Multi-Agent Reinforcement Learning

A practical challenge in reinforcement learning are combinatorial action spaces that make planning computationally demanding. For example, in cooperative multi-agent reinforcement learning, a potentially large number of agents jointly optimize a global reward function, which leads to a combinatorial blow-up in the action space by the number of agents. As a minimal requirement, we assume access to an argmax oracle that allows to efficiently compute the greedy policy for any Q-function in the model class. Building on recent work in planning with local access to a simulator and linear function approximation, we propose efficient algorithms for this setting that lead to polynomial compute and query complexity in all relevant problem parameters. For the special case where the feature decomposition is additive, we further improve the bounds and extend the results to the kernelized setting with an efficient algorithm.