Juliusz Ziomek
Just One Layer Norm Guarantees Stable Extrapolation
May 20, 2025Abstract:In spite of their prevalence, the behaviour of Neural Networks when extrapolating far from the training distribution remains poorly understood, with existing results limited to specific cases. In this work, we prove general results -- the first of their kind -- by applying Neural Tangent Kernel (NTK) theory to analyse infinitely-wide neural networks trained until convergence and prove that the inclusion of just one Layer Norm (LN) fundamentally alters the induced NTK, transforming it into a bounded-variance kernel. As a result, the output of an infinitely wide network with at least one LN remains bounded, even on inputs far from the training data. In contrast, we show that a broad class of networks without LN can produce pathologically large outputs for certain inputs. We support these theoretical findings with empirical experiments on finite-width networks, demonstrating that while standard NNs often exhibit uncontrolled growth outside the training domain, a single LN layer effectively mitigates this instability. Finally, we explore real-world implications of this extrapolatory stability, including applications to predicting residue sizes in proteins larger than those seen during training and estimating age from facial images of underrepresented ethnicities absent from the training set.
Mean-Field Bayesian Optimisation
Feb 17, 2025
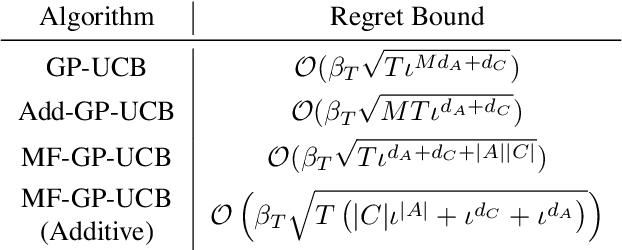
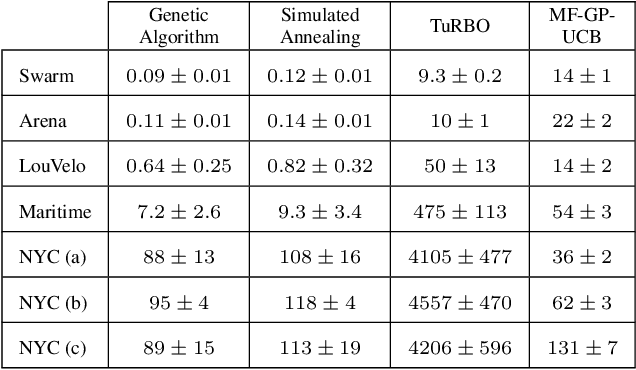
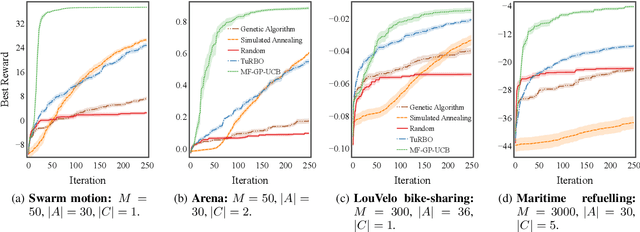
Abstract:We address the problem of optimising the average payoff for a large number of cooperating agents, where the payoff function is unknown and treated as a black box. While standard Bayesian Optimisation (BO) methods struggle with the scalability required for high-dimensional input spaces, we demonstrate how leveraging the mean-field assumption on the black-box function can transform BO into an efficient and scalable solution. Specifically, we introduce MF-GP-UCB, a novel efficient algorithm designed to optimise agent payoffs in this setting. Our theoretical analysis establishes a regret bound for MF-GP-UCB that is independent of the number of agents, contrasting sharply with the exponential dependence observed when naive BO methods are applied. We evaluate our algorithm on a diverse set of tasks, including real-world problems, such as optimising the location of public bikes for a bike-sharing programme, distributing taxi fleets, and selecting refuelling ports for maritime vessels. Empirical results demonstrate that MF-GP-UCB significantly outperforms existing benchmarks, offering substantial improvements in performance and scalability, constituting a promising solution for mean-field, black-box optimisation. The code is available at https://github.com/petarsteinberg/MF-BO.
Distribution Transformers: Fast Approximate Bayesian Inference With On-The-Fly Prior Adaptation
Feb 04, 2025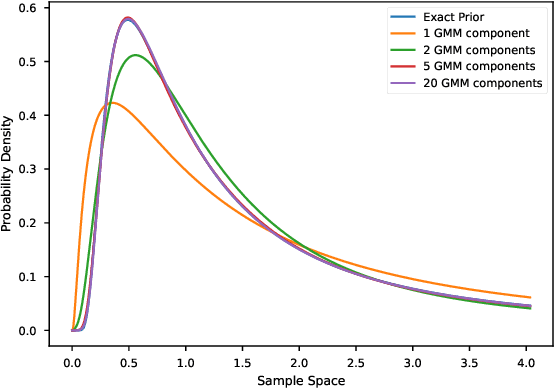

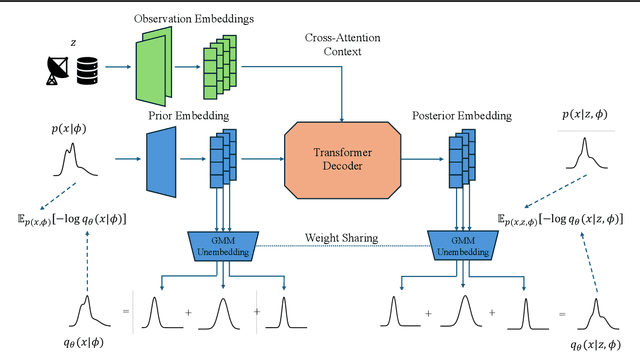

Abstract:While Bayesian inference provides a principled framework for reasoning under uncertainty, its widespread adoption is limited by the intractability of exact posterior computation, necessitating the use of approximate inference. However, existing methods are often computationally expensive, or demand costly retraining when priors change, limiting their utility, particularly in sequential inference problems such as real-time sensor fusion. To address these challenges, we introduce the Distribution Transformer -- a novel architecture that can learn arbitrary distribution-to-distribution mappings. Our method can be trained to map a prior to the corresponding posterior, conditioned on some dataset -- thus performing approximate Bayesian inference. Our novel architecture represents a prior distribution as a (universally-approximating) Gaussian Mixture Model (GMM), and transforms it into a GMM representation of the posterior. The components of the GMM attend to each other via self-attention, and to the datapoints via cross-attention. We demonstrate that Distribution Transformers both maintain flexibility to vary the prior, and significantly reduces computation times-from minutes to milliseconds-while achieving log-likelihood performance on par with or superior to existing approximate inference methods across tasks such as sequential inference, quantum system parameter inference, and Gaussian Process predictive posterior inference with hyperpriors.
Bayesian Optimisation with Unknown Hyperparameters: Regret Bounds Logarithmically Closer to Optimal
Oct 14, 2024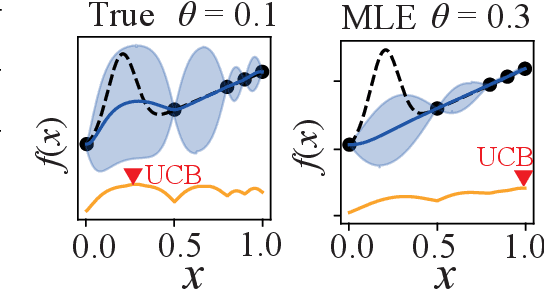

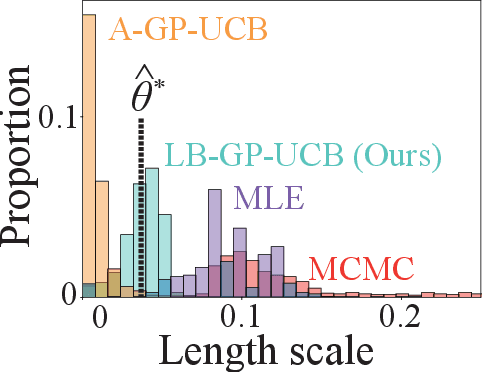
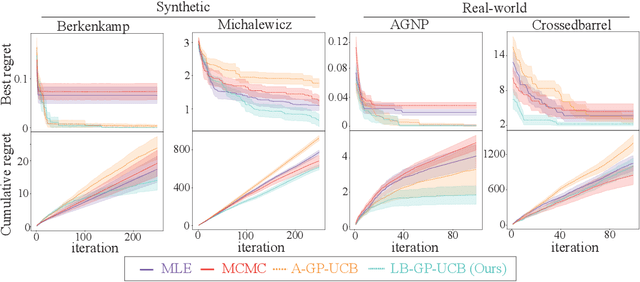
Abstract:Bayesian Optimization (BO) is widely used for optimising black-box functions but requires us to specify the length scale hyperparameter, which defines the smoothness of the functions the optimizer will consider. Most current BO algorithms choose this hyperparameter by maximizing the marginal likelihood of the observed data, albeit risking misspecification if the objective function is less smooth in regions we have not yet explored. The only prior solution addressing this problem with theoretical guarantees was A-GP-UCB, proposed by Berkenkamp et al. (2019). This algorithm progressively decreases the length scale, expanding the class of functions considered by the optimizer. However, A-GP-UCB lacks a stopping mechanism, leading to over-exploration and slow convergence. To overcome this, we introduce Length scale Balancing (LB) - a novel approach, aggregating multiple base surrogate models with varying length scales. LB intermittently adds smaller length scale candidate values while retaining longer scales, balancing exploration and exploitation. We formally derive a cumulative regret bound of LB and compare it with the regret of an oracle BO algorithm using the optimal length scale. Denoting the factor by which the regret bound of A-GP-UCB was away from oracle as $g(T)$, we show that LB is only $\log g(T)$ away from oracle regret. We also empirically evaluate our algorithm on synthetic and real-world benchmarks and show it outperforms A-GP-UCB, maximum likelihood estimation and MCMC.
Beyond Lengthscales: No-regret Bayesian Optimisation With Unknown Hyperparameters Of Any Type
Feb 13, 2024Abstract:Bayesian optimisation requires fitting a Gaussian process model, which in turn requires specifying hyperparameters - most of the theoretical literature assumes those hyperparameters are known. The commonly used maximum likelihood estimator for hyperparameters of the Gaussian process is consistent only if the data fills the space uniformly, which does not have to be the case in Bayesian optimisation. Since no guarantees exist regarding the correctness of hyperparameter estimation, and those hyperparameters can significantly affect the Gaussian process fit, theoretical analysis of Bayesian optimisation with unknown hyperparameters is very challenging. Previously proposed algorithms with the no-regret property were only able to handle the special case of unknown lengthscales, reproducing kernel Hilbert space norm and applied only to the frequentist case. We propose a novel algorithm, HE-GP-UCB, which is the first algorithm enjoying the no-regret property in the case of unknown hyperparameters of arbitrary form, and which supports both Bayesian and frequentist settings. Our proof idea is novel and can easily be extended to other variants of Bayesian optimisation. We show this by extending our algorithm to the adversarially robust optimisation setting under unknown hyperparameters. Finally, we empirically evaluate our algorithm on a set of toy problems and show that it can outperform the maximum likelihood estimator.
Why Can Large Language Models Generate Correct Chain-of-Thoughts?
Oct 30, 2023Abstract:This paper delves into the capabilities of large language models (LLMs), specifically focusing on advancing the theoretical comprehension of chain-of-thought prompting. We investigate how LLMs can be effectively induced to generate a coherent chain of thoughts. To achieve this, we introduce a two-level hierarchical graphical model tailored for natural language generation. Within this framework, we establish a compelling geometrical convergence rate that gauges the likelihood of an LLM-generated chain of thoughts compared to those originating from the true language. Our findings provide a theoretical justification for the ability of LLMs to produce the correct sequence of thoughts (potentially) explaining performance gains in tasks demanding reasoning skills.
Are Random Decompositions all we need in High Dimensional Bayesian Optimisation?
Jan 30, 2023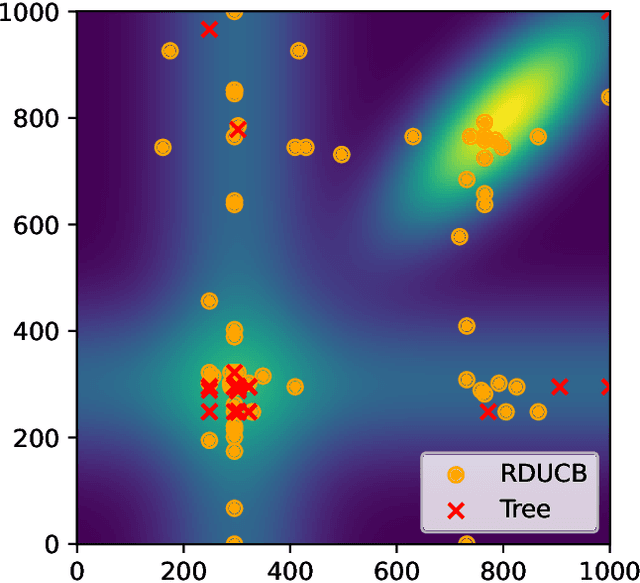
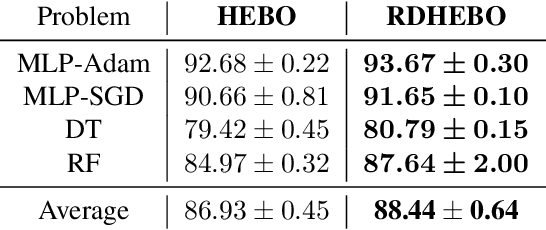
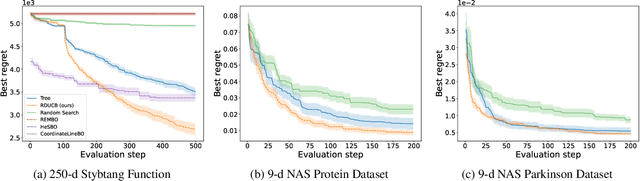
Abstract:Learning decompositions of expensive-to-evaluate black-box functions promises to scale Bayesian optimisation (BO) to high-dimensional problems. However, the success of these techniques depends on finding proper decompositions that accurately represent the black-box. While previous works learn those decompositions based on data, we investigate data-independent decomposition sampling rules in this paper. We find that data-driven learners of decompositions can be easily misled towards local decompositions that do not hold globally across the search space. Then, we formally show that a random tree-based decomposition sampler exhibits favourable theoretical guarantees that effectively trade off maximal information gain and functional mismatch between the actual black-box and its surrogate as provided by the decomposition. Those results motivate the development of the random decomposition upper-confidence bound algorithm (RDUCB) that is straightforward to implement - (almost) plug-and-play - and, surprisingly, yields significant empirical gains compared to the previous state-of-the-art on a comprehensive set of benchmarks. We also confirm the plug-and-play nature of our modelling component by integrating our method with HEBO, showing improved practical gains in the highest dimensional tasks from Bayesmark.
Semi-Centralised Multi-Agent Reinforcement Learning with Policy-Embedded Training
Sep 02, 2022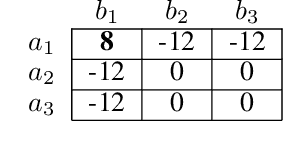
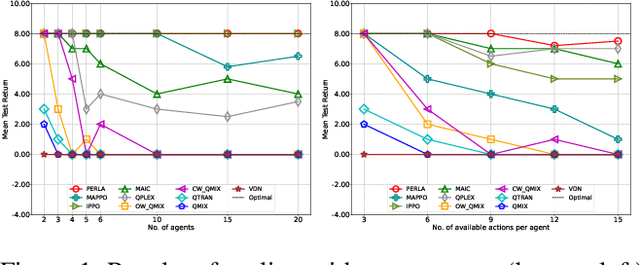
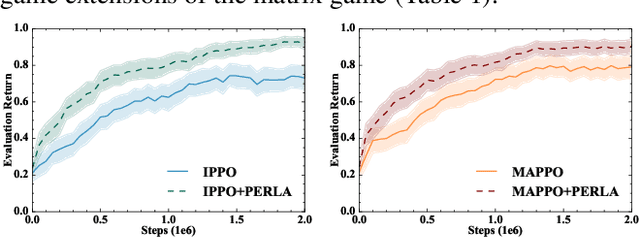
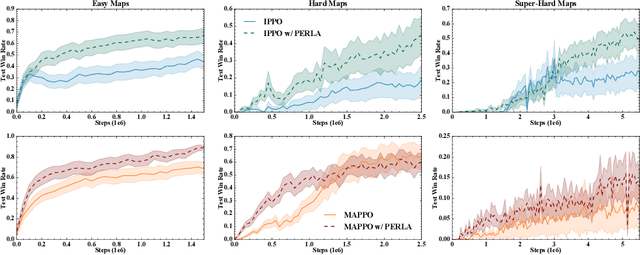
Abstract:Centralised training (CT) is the basis for many popular multi-agent reinforcement learning (MARL) methods because it allows agents to quickly learn high-performing policies. However, CT relies on agents learning from one-off observations of other agents' actions at a given state. Because MARL agents explore and update their policies during training, these observations often provide poor predictions about other agents' behaviour and the expected return for a given action. CT methods therefore suffer from high variance and error-prone estimates, harming learning. CT methods also suffer from explosive growth in complexity due to the reliance on global observations, unless strong factorisation restrictions are imposed (e.g., monotonic reward functions for QMIX). We address these challenges with a new semi-centralised MARL framework that performs policy-embedded training and decentralised execution. Our method, policy embedded reinforcement learning algorithm (PERLA), is an enhancement tool for Actor-Critic MARL algorithms that leverages a novel parameter sharing protocol and policy embedding method to maintain estimates that account for other agents' behaviour. Our theory proves PERLA dramatically reduces the variance in value estimates. Unlike various CT methods, PERLA, which seamlessly adopts MARL algorithms, scales easily with the number of agents without the need for restrictive factorisation assumptions. We demonstrate PERLA's superior empirical performance and efficient scaling in benchmark environments including StarCraft Micromanagement II and Multi-agent Mujoco
Timing is Everything: Learning to Act Selectively with Costly Actions and Budgetary Constraints
Jun 06, 2022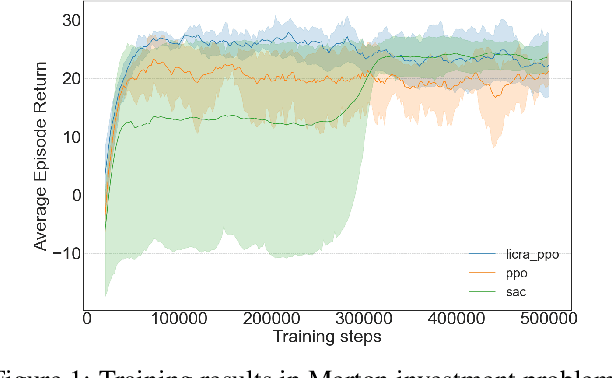
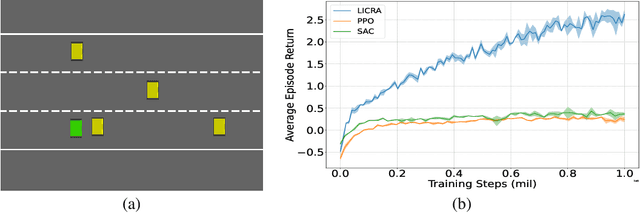
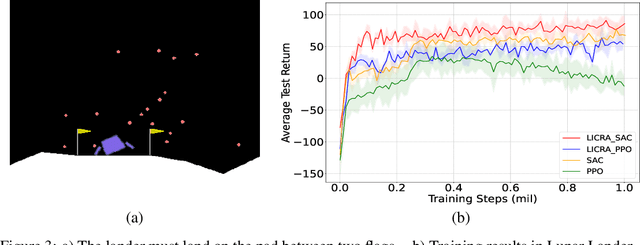
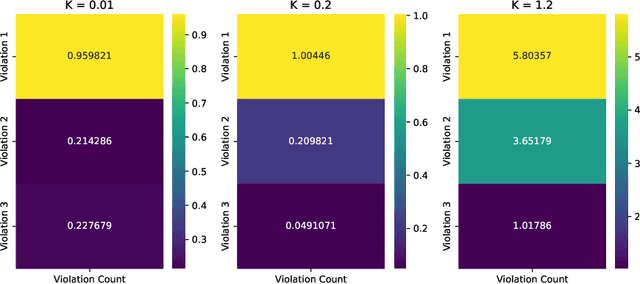
Abstract:Many real-world settings involve costs for performing actions; transaction costs in financial systems and fuel costs being common examples. In these settings, performing actions at each time step quickly accumulates costs leading to vastly suboptimal outcomes. Additionally, repeatedly acting produces wear and tear and ultimately, damage. Determining when to act is crucial for achieving successful outcomes and yet, the challenge of efficiently learning to behave optimally when actions incur minimally bounded costs remains unresolved. In this paper, we introduce a reinforcement learning (RL) framework named Learnable Impulse Control Reinforcement Algorithm (LICRA), for learning to optimally select both when to act and which actions to take when actions incur costs. At the core of LICRA is a nested structure that combines RL and a form of policy known as impulse control which learns to maximise objectives when actions incur costs. We prove that LICRA, which seamlessly adopts any RL method, converges to policies that optimally select when to perform actions and their optimal magnitudes. We then augment LICRA to handle problems in which the agent can perform at most $k<\infty$ actions and more generally, faces a budget constraint. We show LICRA learns the optimal value function and ensures budget constraints are satisfied almost surely. We demonstrate empirically LICRA's superior performance against benchmark RL methods in OpenAI gym's Lunar Lander and in Highway environments and a variant of the Merton portfolio problem within finance.
Modelling nonlinear dependencies in the latent space of inverse scattering
Mar 19, 2022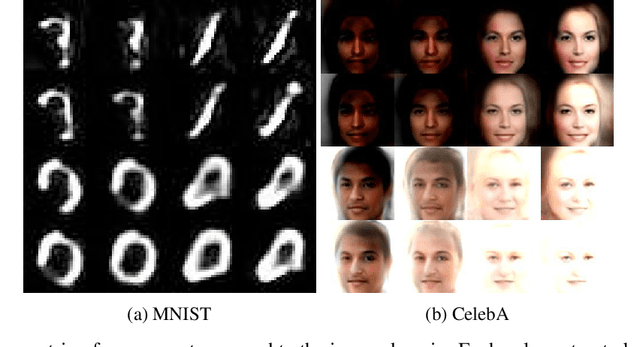



Abstract:The problem of inverse scattering proposed by Angles and Mallat in 2018, concerns training a deep neural network to invert the scattering transform applied to an image. After such a network is trained, it can be used as a generative model given that we can sample from the distribution of principal components of scattering coefficients. For this purpose, Angles and Mallat simply use samples from independent Gaussians. However, as shown in this paper, the distribution of interest can actually be very far from normal and non-negligible dependencies might exist between different coefficients. This motivates using models for this distribution that allow for non-linear dependencies between variables. Within this paper, two such models are explored, namely a Variational AutoEncoder and a Generative Adversarial Network. We demonstrate the results obtained can be extremely realistic on some datasets and look better than those produced by Angles and Mallat. The conducted meta-analysis also shows a clear practical advantage of such constructed generative models in terms of the efficiency of their training process compared to existing generative models for images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge