Michael A Osborne
Fixing the Pitfalls of Probabilistic Time-Series Forecasting Evaluation by Kernel Quadrature
Mar 08, 2025Abstract:Despite the significance of probabilistic time-series forecasting models, their evaluation metrics often involve intractable integrations. The most widely used metric, the continuous ranked probability score (CRPS), is a strictly proper scoring function; however, its computation requires approximation. We found that popular CRPS estimators--specifically, the quantile-based estimator implemented in the widely used GluonTS library and the probability-weighted moment approximation--both exhibit inherent estimation biases. These biases lead to crude approximations, resulting in improper rankings of forecasting model performance when CRPS values are close. To address this issue, we introduced a kernel quadrature approach that leverages an unbiased CRPS estimator and employs cubature construction for scalable computation. Empirically, our approach consistently outperforms the two widely used CRPS estimators.
Distribution Transformers: Fast Approximate Bayesian Inference With On-The-Fly Prior Adaptation
Feb 04, 2025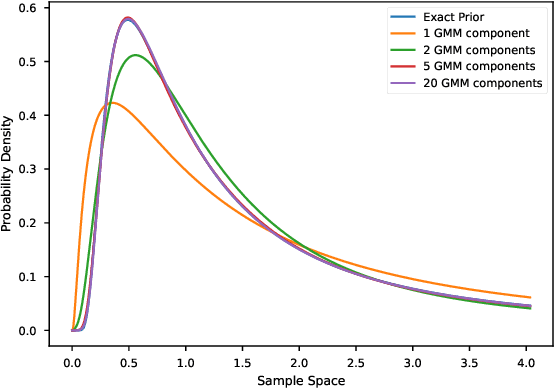

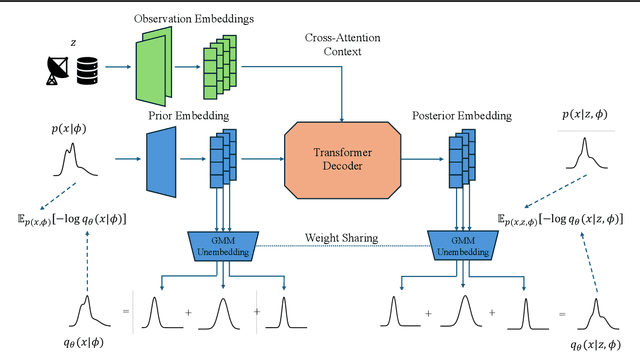

Abstract:While Bayesian inference provides a principled framework for reasoning under uncertainty, its widespread adoption is limited by the intractability of exact posterior computation, necessitating the use of approximate inference. However, existing methods are often computationally expensive, or demand costly retraining when priors change, limiting their utility, particularly in sequential inference problems such as real-time sensor fusion. To address these challenges, we introduce the Distribution Transformer -- a novel architecture that can learn arbitrary distribution-to-distribution mappings. Our method can be trained to map a prior to the corresponding posterior, conditioned on some dataset -- thus performing approximate Bayesian inference. Our novel architecture represents a prior distribution as a (universally-approximating) Gaussian Mixture Model (GMM), and transforms it into a GMM representation of the posterior. The components of the GMM attend to each other via self-attention, and to the datapoints via cross-attention. We demonstrate that Distribution Transformers both maintain flexibility to vary the prior, and significantly reduces computation times-from minutes to milliseconds-while achieving log-likelihood performance on par with or superior to existing approximate inference methods across tasks such as sequential inference, quantum system parameter inference, and Gaussian Process predictive posterior inference with hyperpriors.
Optimal Transport Kernels for Sequential and Parallel Neural Architecture Search
Jun 13, 2020



Abstract:Neural architecture search (NAS) automates the design of deep neural networks. One of the main challenges in searching complex and non-continuous architectures is to compare the similarity of networks that the conventional Euclidean metric may fail to capture. Optimal transport (OT) is resilient to such complex structure by considering the minimal cost for transporting a network into another. However, the OT is generally not negative definite which may limit its ability to build the positive-definite kernels required in many kernel-dependent frameworks. Building upon tree-Wasserstein (TW), which is a negative definite variant of OT, we develop a novel discrepancy for neural architectures, and demonstrate it within a Gaussian process surrogate model for the sequential NAS settings. Furthermore, we derive a novel parallel NAS, using quality k-determinantal point process on the GP posterior, to select diverse and high-performing architectures from a discrete set of candidates. Empirically, we demonstrate that our TW-based approaches outperform other baselines in both sequential and parallel NAS.
Bayesian Optimization for Iterative Learning
Oct 07, 2019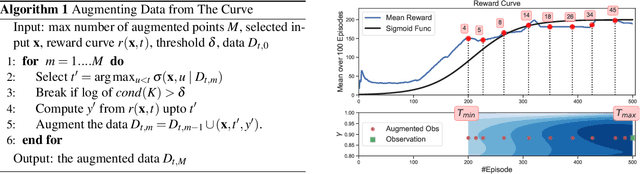
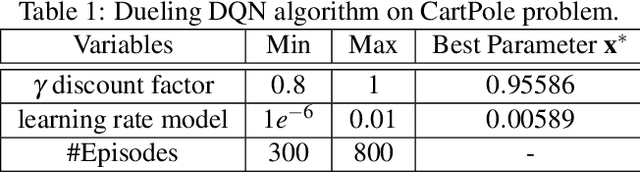


Abstract:The success of deep (reinforcement) learning systems crucially depends on the correct choice of hyperparameters which are notoriously sensitive and expensive to evaluate. Training these systems typically requires running iterative processes over multiple epochs or episodes. Traditional approaches only consider final performances of a hyperparameter although intermediate information from the learning curve is readily available. In this paper, we present a Bayesian optimization approach which exploits the iterative structure of learning algorithms for efficient hyperparameter tuning. First, we transform each training curve into a numeric score. Second, we selectively augment the data using the auxiliary information from the curve. This augmentation step enables modeling efficiency while preventing the ill-conditioned issue of Gaussian process covariance matrix happened when adding the whole curve. We demonstrate the efficiency of our algorithm by tuning hyperparameters for the training of deep reinforcement learning agents and convolutional neural networks. Our algorithm outperforms all existing baselines in identifying optimal hyperparameters in minimal time.
AReS and MaRS - Adversarial and MMD-Minimizing Regression for SDEs
Feb 22, 2019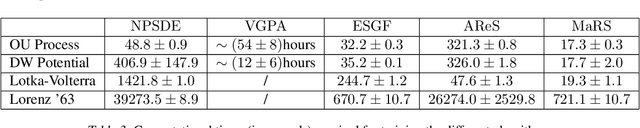
Abstract:Stochastic differential equations are an important modeling class in many disciplines. Consequently, there exist many methods relying on various discretization and numerical integration schemes. In this paper, we propose a novel, probabilistic model for estimating the drift and diffusion given noisy observations of the underlying stochastic system. Using state-of-the-art adversarial and moment matching inference techniques, we circumvent the use of the discretization schemes as seen in classical approaches. This yields significant improvements in parameter estimation accuracy and robustness given random initial guesses. On four commonly used benchmark systems, we demonstrate the performance of our algorithms compared to state-of-the-art solutions based on extended Kalman filtering and Gaussian processes.
ODIN: ODE-Informed Regression for Parameter and State Inference in Time-Continuous Dynamical Systems
Feb 17, 2019
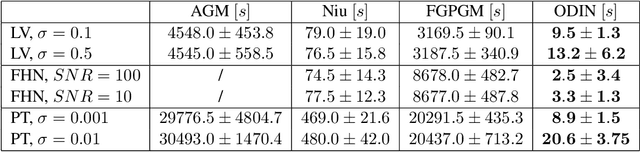
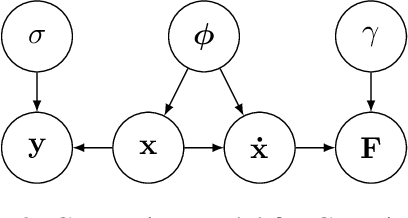

Abstract:Parameter inference in ordinary differential equations is an important problem in many applied sciences and in engineering, especially in a data-scarce setting. In this work, we introduce a novel generative modeling approach based on constrained Gaussian processes and use it to create a computationally and data efficient algorithm for state and parameter inference. In an extensive set of experiments, our approach outperforms its competitors both in terms of accuracy and computational cost for parameter inference. It also shows promising results for the much more challenging problem of model selection.
Blitzkriging: Kronecker-structured Stochastic Gaussian Processes
Oct 31, 2015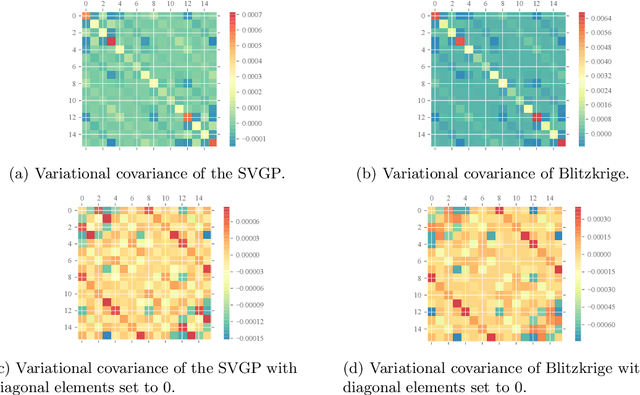

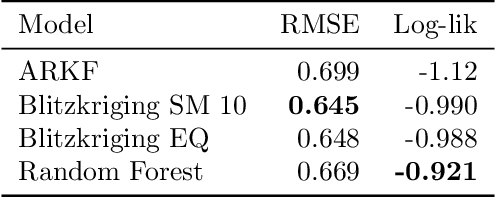
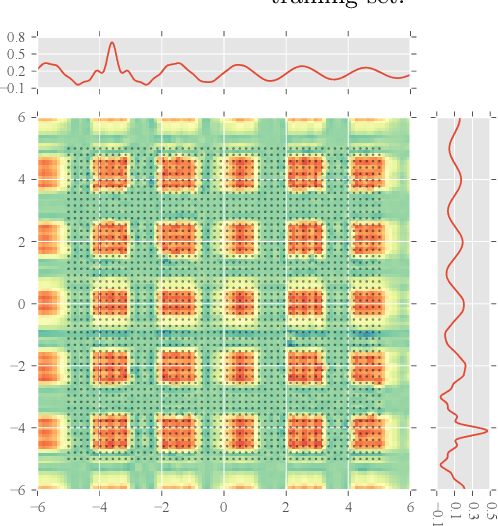
Abstract:We present Blitzkriging, a new approach to fast inference for Gaussian processes, applicable to regression, optimisation and classification. State-of-the-art (stochastic) inference for Gaussian processes on very large datasets scales cubically in the number of 'inducing inputs', variables introduced to factorise the model. Blitzkriging shares state-of-the-art scaling with data, but reduces the scaling in the number of inducing points to approximately linear. Further, in contrast to other methods, Blitzkriging: does not force the data to conform to any particular structure (including grid-like); reduces reliance on error-prone optimisation of inducing point locations; and is able to learn rich (covariance) structure from the data. We demonstrate the benefits of our approach on real data in regression, time-series prediction and signal-interpolation experiments.
Probabilistic Numerics and Uncertainty in Computations
Jun 03, 2015



Abstract:We deliver a call to arms for probabilistic numerical methods: algorithms for numerical tasks, including linear algebra, integration, optimization and solving differential equations, that return uncertainties in their calculations. Such uncertainties, arising from the loss of precision induced by numerical calculation with limited time or hardware, are important for much contemporary science and industry. Within applications such as climate science and astrophysics, the need to make decisions on the basis of computations with large and complex data has led to a renewed focus on the management of numerical uncertainty. We describe how several seminal classic numerical methods can be interpreted naturally as probabilistic inference. We then show that the probabilistic view suggests new algorithms that can flexibly be adapted to suit application specifics, while delivering improved empirical performance. We provide concrete illustrations of the benefits of probabilistic numeric algorithms on real scientific problems from astrometry and astronomical imaging, while highlighting open problems with these new algorithms. Finally, we describe how probabilistic numerical methods provide a coherent framework for identifying the uncertainty in calculations performed with a combination of numerical algorithms (e.g. both numerical optimisers and differential equation solvers), potentially allowing the diagnosis (and control) of error sources in computations.
Automated Machine Learning on Big Data using Stochastic Algorithm Tuning
Jul 30, 2014
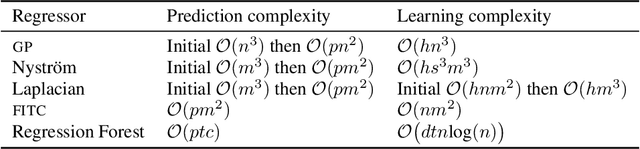


Abstract:We introduce a means of automating machine learning (ML) for big data tasks, by performing scalable stochastic Bayesian optimisation of ML algorithm parameters and hyper-parameters. More often than not, the critical tuning of ML algorithm parameters has relied on domain expertise from experts, along with laborious hand-tuning, brute search or lengthy sampling runs. Against this background, Bayesian optimisation is finding increasing use in automating parameter tuning, making ML algorithms accessible even to non-experts. However, the state of the art in Bayesian optimisation is incapable of scaling to the large number of evaluations of algorithm performance required to fit realistic models to complex, big data. We here describe a stochastic, sparse, Bayesian optimisation strategy to solve this problem, using many thousands of noisy evaluations of algorithm performance on subsets of data in order to effectively train algorithms for big data. We provide a comprehensive benchmarking of possible sparsification strategies for Bayesian optimisation, concluding that a Nystrom approximation offers the best scaling and performance for real tasks. Our proposed algorithm demonstrates substantial improvement over the state of the art in tuning the parameters of a Gaussian Process time series prediction task on real, big data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge