Bayesian Optimization for Iterative Learning

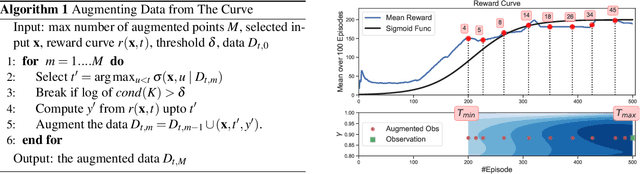
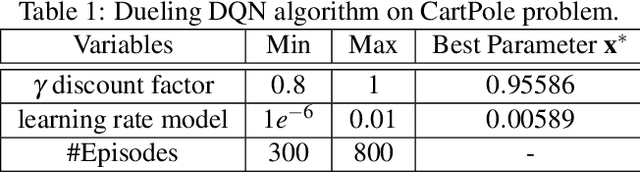
The success of deep (reinforcement) learning systems crucially depends on the correct choice of hyperparameters which are notoriously sensitive and expensive to evaluate. Training these systems typically requires running iterative processes over multiple epochs or episodes. Traditional approaches only consider final performances of a hyperparameter although intermediate information from the learning curve is readily available. In this paper, we present a Bayesian optimization approach which exploits the iterative structure of learning algorithms for efficient hyperparameter tuning. First, we transform each training curve into a numeric score. Second, we selectively augment the data using the auxiliary information from the curve. This augmentation step enables modeling efficiency while preventing the ill-conditioned issue of Gaussian process covariance matrix happened when adding the whole curve. We demonstrate the efficiency of our algorithm by tuning hyperparameters for the training of deep reinforcement learning agents and convolutional neural networks. Our algorithm outperforms all existing baselines in identifying optimal hyperparameters in minimal time.