Generative Modeling through Spectral Analysis of Koopman Operator

We propose Koopman Spectral Wasserstein Gradient Descent (KSWGD), a generative modeling framework that combines operator-theoretic spectral analysis with optimal transport. The novel insight is that the spectral structure required for accelerated Wasserstein gradient descent can be directly estimated from trajectory data via Koopman operator approximation which can eliminate the need for explicit knowledge of the target potential or neural network training. We provide rigorous convergence analysis and establish connection to Feynman-Kac theory that clarifies the method's probabilistic foundation. Experiments across diverse settings, including compact manifold sampling, metastable multi-well systems, image generation, and high dimensional stochastic partial differential equation, demonstrate that KSWGD consistently achieves faster convergence than other existing methods while maintaining high sample quality.

Scalable Valuation of Human Feedback through Provably Robust Model Alignment

Despite the importance of aligning language models with human preferences, crowd-sourced human feedback is often noisy -- for example, preferring less desirable responses -- posing a fundamental challenge to alignment. A truly robust alignment objective should yield identical model parameters even under severe label noise, a property known as redescending. We prove that no existing alignment methods satisfy this property. To address this, we propose H\"older-DPO, the first principled alignment loss with a provable redescending property, enabling estimation of the clean data distribution from noisy feedback. The aligned model estimates the likelihood of clean data, providing a theoretically grounded metric for dataset valuation that identifies the location and fraction of mislabels. This metric is gradient-free, enabling scalable and automated human feedback valuation without costly manual verification or clean validation dataset. H\"older-DPO achieves state-of-the-art robust alignment performance while accurately detecting mislabels in controlled datasets. Finally, we apply H\"older-DPO to widely used alignment datasets, revealing substantial noise levels and demonstrating that removing these mislabels significantly improves alignment performance across methods.

Fixing the Pitfalls of Probabilistic Time-Series Forecasting Evaluation by Kernel Quadrature

Despite the significance of probabilistic time-series forecasting models, their evaluation metrics often involve intractable integrations. The most widely used metric, the continuous ranked probability score (CRPS), is a strictly proper scoring function; however, its computation requires approximation. We found that popular CRPS estimators--specifically, the quantile-based estimator implemented in the widely used GluonTS library and the probability-weighted moment approximation--both exhibit inherent estimation biases. These biases lead to crude approximations, resulting in improper rankings of forecasting model performance when CRPS values are close. To address this issue, we introduced a kernel quadrature approach that leverages an unbiased CRPS estimator and employs cubature construction for scalable computation. Empirically, our approach consistently outperforms the two widely used CRPS estimators.

PAC-Bayes Analysis for Recalibration in Classification

Nonparametric estimation with binning is widely employed in the calibration error evaluation and the recalibration of machine learning models. Recently, theoretical analyses of the bias induced by this estimation approach have been actively pursued; however, the understanding of the generalization of the calibration error to unknown data remains limited. In addition, although many recalibration algorithms have been proposed, their generalization performance lacks theoretical guarantees. To address this problem, we conduct a generalization analysis of the calibration error under the probably approximately correct (PAC) Bayes framework. This approach enables us to derive a first optimizable upper bound for the generalization error in the calibration context. We then propose a generalization-aware recalibration algorithm based on our generalization theory. Numerical experiments show that our algorithm improves the Gaussian-process-based recalibration performance on various benchmark datasets and models.

Time-Independent Information-Theoretic Generalization Bounds for SGLD

We provide novel information-theoretic generalization bounds for stochastic gradient Langevin dynamics (SGLD) under the assumptions of smoothness and dissipativity, which are widely used in sampling and non-convex optimization studies. Our bounds are time-independent and decay to zero as the sample size increases, regardless of the number of iterations and whether the step size is fixed. Unlike previous studies, we derive the generalization error bounds by focusing on the time evolution of the Kullback--Leibler divergence, which is related to the stability of datasets and is the upper bound of the mutual information between output parameters and an input dataset. Additionally, we establish the first information-theoretic generalization bound when the training and test loss are the same by showing that a loss function of SGLD is sub-exponential. This bound is also time-independent and removes the problematic step size dependence in existing work, leading to an improved excess risk bound by combining our analysis with the existing non-convex optimization error bounds.

Initialization Bias of Fourier Neural Operator: Revisiting the Edge of Chaos

This paper investigates the initialization bias of the Fourier neural operator (FNO). A mean-field theory for FNO is established, analyzing the behavior of the random FNO from an ``edge of chaos'' perspective. We uncover that the forward and backward propagation behaviors exhibit characteristics unique to FNO, induced by mode truncation, while also showcasing similarities to those of densely connected networks. Building upon this observation, we also propose a FNO version of the He initialization scheme to mitigate the negative initialization bias leading to training instability. Experimental results demonstrate the effectiveness of our initialization scheme, enabling stable training of a 32-layer FNO without the need for additional techniques or significant performance degradation.

$γ$-ABC: Outlier-Robust Approximate Bayesian Computation based on Robust Divergence Estimator

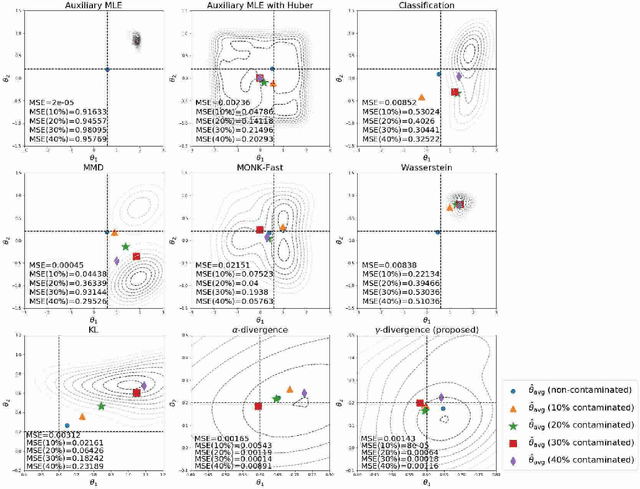
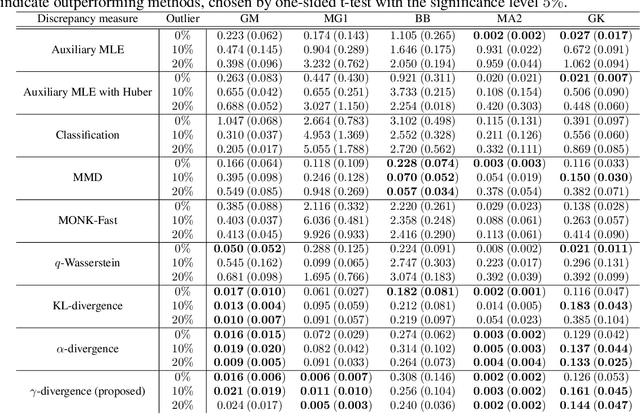
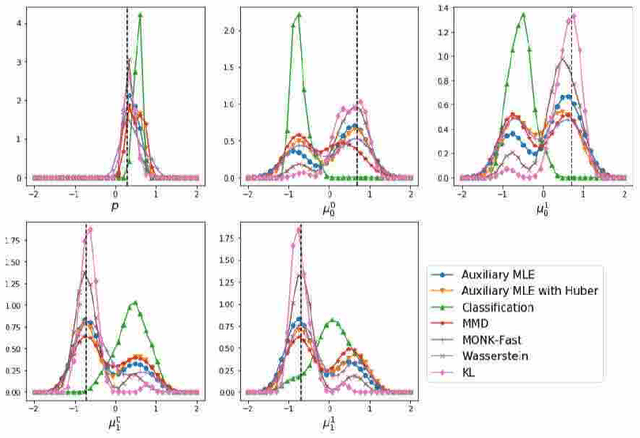
Making a reliable inference in complex models is an essential issue in statistical modeling. However, approximate Bayesian computation (ABC) proposed for highly complex models that have uncomputable likelihood is greatly affected by the sensitivity of the data discrepancy to outliers. Even using a data discrepancy with robust functions such as the Huber function does not entirely bypass its negative effects. In this paper, we propose a novel divergence estimator based on robust divergence and to use it as a data discrepancy in the ABC framework. Furthermore, we show that our estimator has an effective robustness property, known as the redescending property. Our estimator also enjoys ideal properties such as asymptotic unbiasedness, almost sure convergence, and linear time complexity. In ABC experiments on several models, we confirm that our method obtains a value closer to the true parameters than that of other discrepancy measures.

Multi-level Monte Carlo Variational Inference

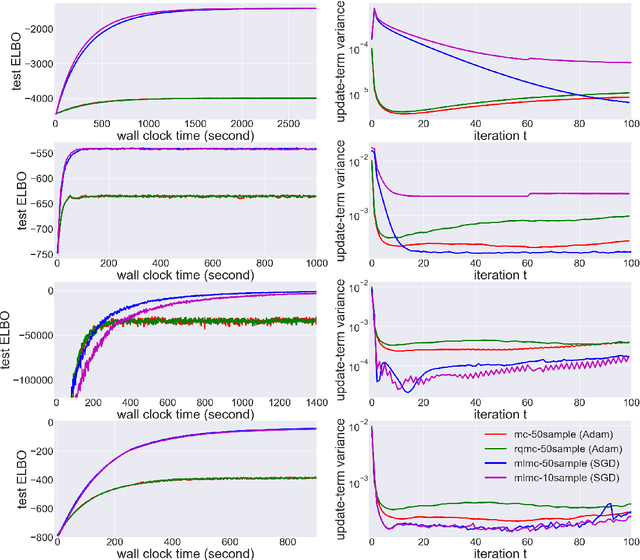
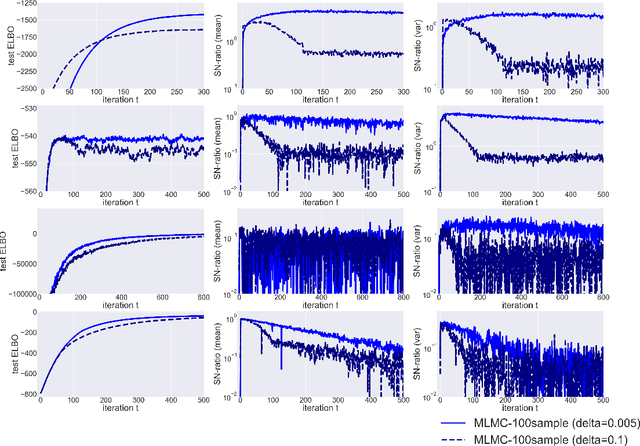
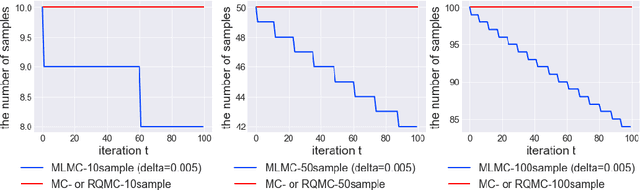
In many statistics and machine learning frameworks, stochastic optimization with high variance gradients has become an important problem. For example, the performance of Monte Carlo variational inference (MCVI) seriously depends on the variance of its stochastic gradient estimator. In this paper, we focused on this problem and proposed a novel framework of variance reduction using multi-level Monte Carlo (MLMC) method. The framework is naturally compatible with reparameterization gradient estimators, which are one of the efficient variance reduction techniques that use the reparameterization trick. We also proposed a novel MCVI algorithm for stochastic gradient estimation on MLMC method in which sample size $N$ is adaptively estimated according to the ratio of the variance and computational cost for each iteration. We furthermore proved that, in our method, the norm of the gradient could converge to $0$ asymptotically. Finally, we evaluated our method by comparing it with benchmark methods in several experiments and showed that our method was able to reduce gradient variance and sampling cost efficiently and be closer to the optimum value than the other methods were.