Universal approximation property of invertible neural networks

Invertible neural networks (INNs) are neural network architectures with invertibility by design. Thanks to their invertibility and the tractability of Jacobian, INNs have various machine learning applications such as probabilistic modeling, generative modeling, and representation learning. However, their attractive properties often come at the cost of restricting the layer designs, which poses a question on their representation power: can we use these models to approximate sufficiently diverse functions? To answer this question, we have developed a general theoretical framework to investigate the representation power of INNs, building on a structure theorem of differential geometry. The framework simplifies the approximation problem of diffeomorphisms, which enables us to show the universal approximation properties of INNs. We apply the framework to two representative classes of INNs, namely Coupling-Flow-based INNs (CF-INNs) and Neural Ordinary Differential Equations (NODEs), and elucidate their high representation power despite the restrictions on their architectures.

Rethinking Importance Weighting for Transfer Learning

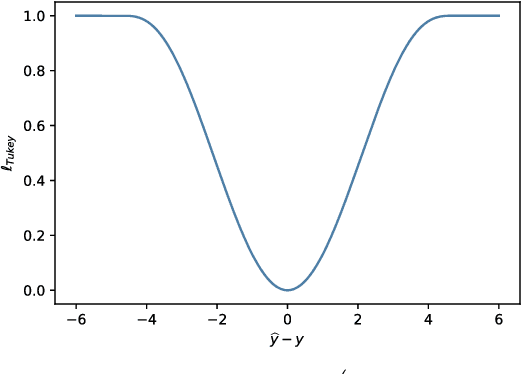
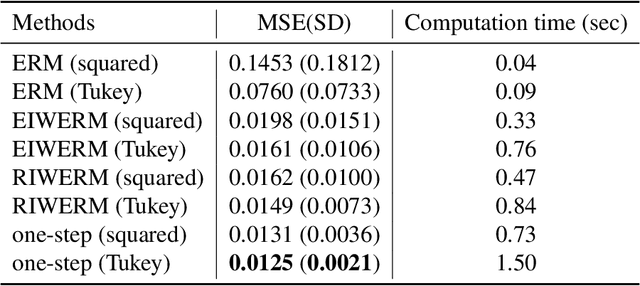
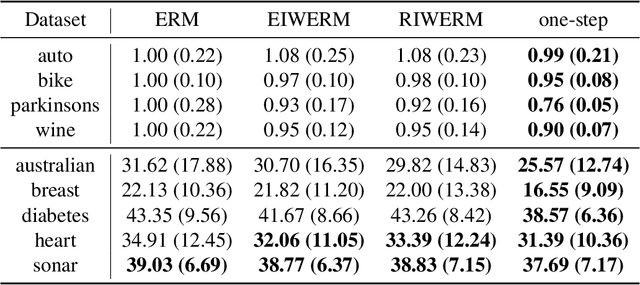
A key assumption in supervised learning is that training and test data follow the same probability distribution. However, this fundamental assumption is not always satisfied in practice, e.g., due to changing environments, sample selection bias, privacy concerns, or high labeling costs. Transfer learning (TL) relaxes this assumption and allows us to learn under distribution shift. Classical TL methods typically rely on importance-weighting -- a predictor is trained based on the training losses weighted according to the importance (i.e., the test-over-training density ratio). However, as real-world machine learning tasks are becoming increasingly complex, high-dimensional, and dynamical, novel approaches are explored to cope with such challenges recently. In this article, after introducing the foundation of TL based on importance-weighting, we review recent advances based on joint and dynamic importance-predictor estimation. Furthermore, we introduce a method of causal mechanism transfer that incorporates causal structure in TL. Finally, we discuss future perspectives of TL research.

Incorporating Causal Graphical Prior Knowledge into Predictive Modeling via Simple Data Augmentation

Causal graphs (CGs) are compact representations of the knowledge of the data generating processes behind the data distributions. When a CG is available, e.g., from the domain knowledge, we can infer the conditional independence (CI) relations that should hold in the data distribution. However, it is not straightforward how to incorporate this knowledge into predictive modeling. In this work, we propose a model-agnostic data augmentation method that allows us to exploit the prior knowledge of the CI encoded in a CG for supervised machine learning. We theoretically justify the proposed method by providing an excess risk bound indicating that the proposed method suppresses overfitting by reducing the apparent complexity of the predictor hypothesis class. Using real-world data with CGs provided by domain experts, we experimentally show that the proposed method is effective in improving the prediction accuracy, especially in the small-data regime.

Universal Approximation Property of Neural Ordinary Differential Equations

Neural ordinary differential equations (NODEs) is an invertible neural network architecture promising for its free-form Jacobian and the availability of a tractable Jacobian determinant estimator. Recently, the representation power of NODEs has been partly uncovered: they form an $L^p$-universal approximator for continuous maps under certain conditions. However, the $L^p$-universality may fail to guarantee an approximation for the entire input domain as it may still hold even if the approximator largely differs from the target function on a small region of the input space. To further uncover the potential of NODEs, we show their stronger approximation property, namely the $\sup$-universality for approximating a large class of diffeomorphisms. It is shown by leveraging a structure theorem of the diffeomorphism group, and the result complements the existing literature by establishing a fairly large set of mappings that NODEs can approximate with a stronger guarantee.

Coupling-based Invertible Neural Networks Are Universal Diffeomorphism Approximators

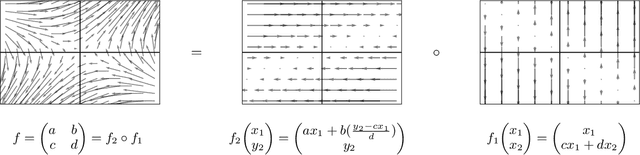
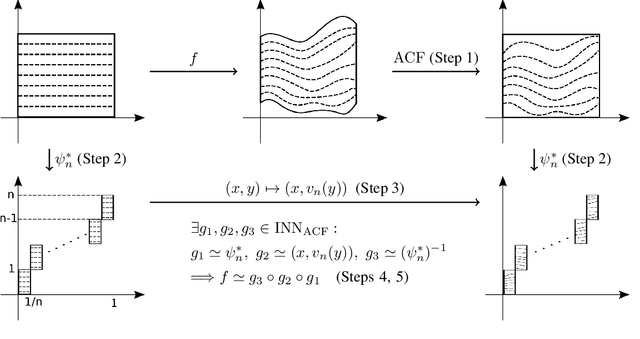
Invertible neural networks based on coupling flows (CF-INNs) have various machine learning applications such as image synthesis and representation learning. However, their desirable characteristics such as analytic invertibility come at the cost of restricting the functional forms. This poses a question on their representation power: are CF-INNs universal approximators for invertible functions? Without a universality, there could be a well-behaved invertible transformation that the CF-INN can never approximate, hence it would render the model class unreliable. We answer this question by showing a convenient criterion: a CF-INN is universal if its layers contain affine coupling and invertible linear functions as special cases. As its corollary, we can affirmatively resolve a previously unsolved problem: whether normalizing flow models based on affine coupling can be universal distributional approximators. In the course of proving the universality, we prove a general theorem to show the equivalence of the universality for certain diffeomorphism classes, a theoretical insight that is of interest by itself.

Non-Negative Bregman Divergence Minimization for Deep Direct Density Ratio Estimation

The estimation of the ratio of two probability densities has garnered attention as the density ratio is useful in various machine learning tasks, such as anomaly detection and domain adaptation. To estimate the density ratio, methods collectively known as direct density ratio estimation (DRE) have been explored. These methods are based on the minimization of the Bregman (BR) divergence between a density ratio model and the true density ratio. However, existing direct DRE suffers from serious overfitting when using flexible models such as neural networks. In this paper, we introduce a non-negative correction for empirical risk using only the prior knowledge of the upper bound of the density ratio. This correction makes a DRE method more robust against overfitting and enables the use of flexible models. In the theoretical analysis, we discuss the consistency of the empirical risk. In our experiments, the proposed estimators show favorable performance in inlier-based outlier detection and covariate shift adaptation.

$γ$-ABC: Outlier-Robust Approximate Bayesian Computation based on Robust Divergence Estimator

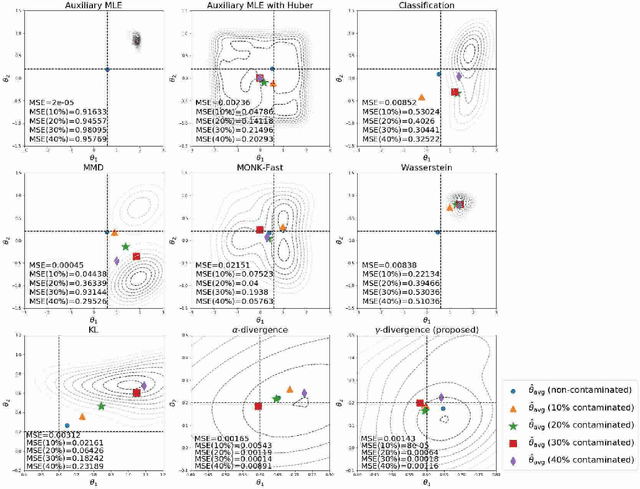
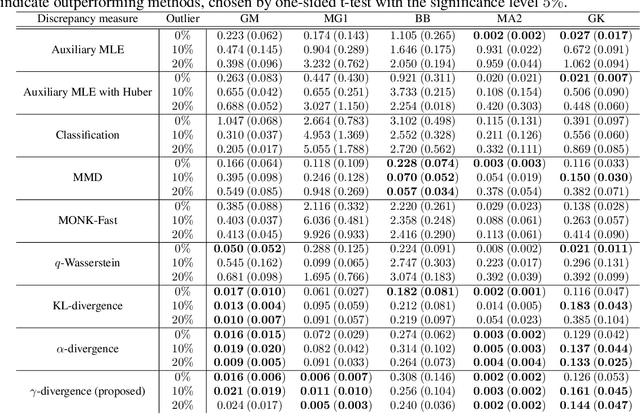
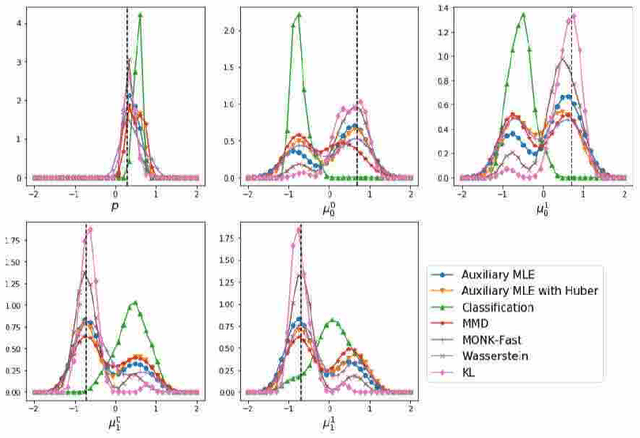
Making a reliable inference in complex models is an essential issue in statistical modeling. However, approximate Bayesian computation (ABC) proposed for highly complex models that have uncomputable likelihood is greatly affected by the sensitivity of the data discrepancy to outliers. Even using a data discrepancy with robust functions such as the Huber function does not entirely bypass its negative effects. In this paper, we propose a novel divergence estimator based on robust divergence and to use it as a data discrepancy in the ABC framework. Furthermore, we show that our estimator has an effective robustness property, known as the redescending property. Our estimator also enjoys ideal properties such as asymptotic unbiasedness, almost sure convergence, and linear time complexity. In ABC experiments on several models, we confirm that our method obtains a value closer to the true parameters than that of other discrepancy measures.

Few-shot Domain Adaptation by Causal Mechanism Transfer

We study few-shot supervised domain adaptation (DA) for regression problems, where only a few labeled target domain data and many labeled source domain data are available. Many of the current DA methods base their transfer assumptions on either parametrized distribution shift or apparent distribution similarities, e.g., identical conditionals or small distributional discrepancies. However, these assumptions may preclude the possibility of adaptation from intricately shifted and apparently very different distributions. To overcome this problem, we propose mechanism transfer, a meta-distributional scenario in which a data generating mechanism is invariant among domains. This transfer assumption can accommodate nonparametric shifts resulting in apparently different distributions while providing a solid statistical basis for DA. We take the structural equations in causal modeling as an example and propose a novel DA method, which is shown to be useful both theoretically and experimentally. Our method can be seen as the first attempt to fully leverage the structural causal models for DA.

Clipped Matrix Completion: a Remedy for Ceiling Effects

We consider the recovery of a low-rank matrix from its clipped observations. Clipping is a common prohibiting factor in many scientific areas that obstructs statistical analyses. On the other hand, matrix completion (MC) methods can recover a low-rank matrix from various information deficits by using the principle of low-rank completion. However, the current theoretical guarantees for low-rank MC do not apply to clipped matrices, as the deficit depends on the underlying values. Therefore, the feasibility of clipped matrix completion (CMC) is not trivial. In this paper, we first provide a theoretical guarantee for an exact recovery of CMC by using a trace norm minimization algorithm. Furthermore, we introduce practical CMC algorithms by extending MC methods. The simple idea is to use the squared hinge loss in place of the squared loss well used in MC methods for reducing the penalty of over-estimation on clipped entries. We also propose a novel regularization term tailored for CMC. It is a combination of two trace norm terms, and we theoretically bound the recovery error under the regularization. We demonstrate the effectiveness of the proposed methods through experiments using both synthetic data and real-world benchmark data for recommendation systems.