Virtual Human Generative Model: Masked Modeling Approach for Learning Human Characteristics

Identifying the relationship between healthcare attributes, lifestyles, and personality is vital for understanding and improving physical and mental conditions. Machine learning approaches are promising for modeling their relationships and offering actionable suggestions. In this paper, we propose Virtual Human Generative Model (VHGM), a machine learning model for estimating attributes about healthcare, lifestyles, and personalities. VHGM is a deep generative model trained with masked modeling to learn the joint distribution of attributes conditioned on known ones. Using heterogeneous tabular datasets, VHGM learns more than 1,800 attributes efficiently. We numerically evaluate the performance of VHGM and its training techniques. As a proof-of-concept of VHGM, we present several applications demonstrating user scenarios, such as virtual measurements of healthcare attributes and hypothesis verifications of lifestyles.

Controlling Posterior Collapse by an Inverse Lipschitz Constraint on the Decoder Network

Variational autoencoders (VAEs) are one of the deep generative models that have experienced enormous success over the past decades. However, in practice, they suffer from a problem called posterior collapse, which occurs when the encoder coincides, or collapses, with the prior taking no information from the latent structure of the input data into consideration. In this work, we introduce an inverse Lipschitz neural network into the decoder and, based on this architecture, provide a new method that can control in a simple and clear manner the degree of posterior collapse for a wide range of VAE models equipped with a concrete theoretical guarantee. We also illustrate the effectiveness of our method through several numerical experiments.

TabRet: Pre-training Transformer-based Tabular Models for Unseen Columns

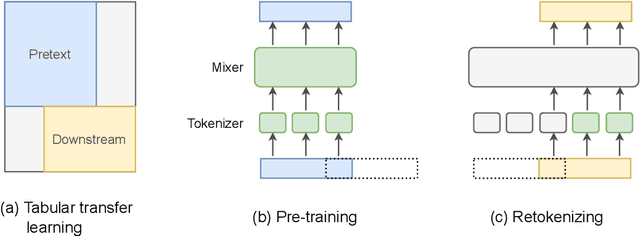
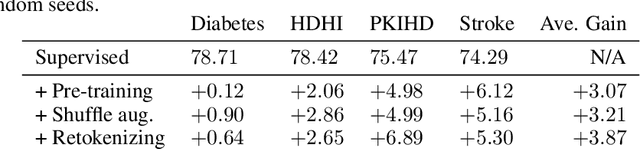
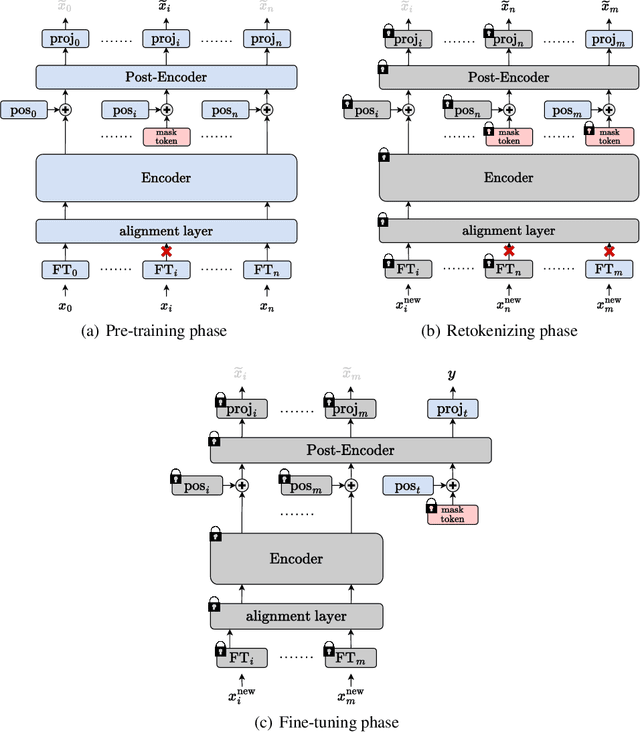
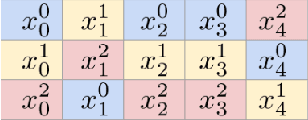
We present \emph{TabRet}, a pre-trainable Transformer-based model for tabular data. TabRet is designed to work on a downstream task that contains columns not seen in pre-training. Unlike other methods, TabRet has an extra learning step before fine-tuning called \emph{retokenizing}, which calibrates feature embeddings based on the masked autoencoding loss. In experiments, we pre-trained TabRet with a large collection of public health surveys and fine-tuned it on classification tasks in healthcare, and TabRet achieved the best AUC performance on four datasets. In addition, an ablation study shows retokenizing and random shuffle augmentation of columns during pre-training contributed to performance gains. The code is available at https://github.com/pfnet-research/tabret .

Universal approximation property of invertible neural networks

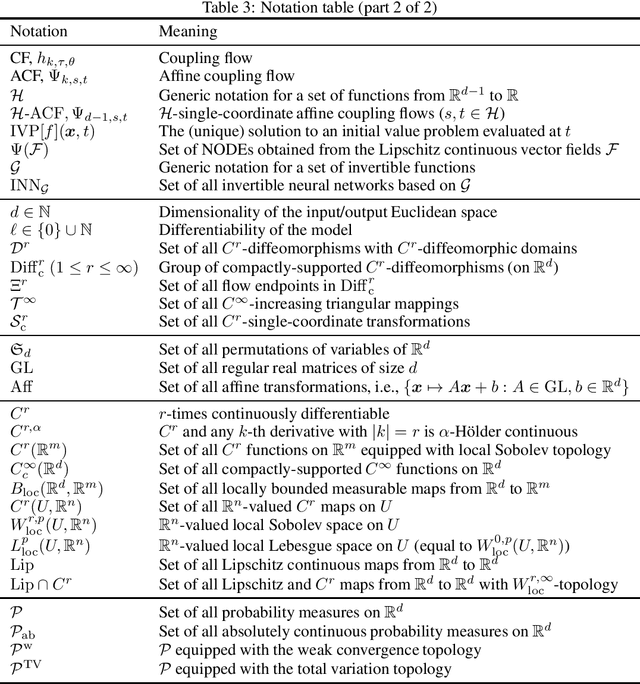
Invertible neural networks (INNs) are neural network architectures with invertibility by design. Thanks to their invertibility and the tractability of Jacobian, INNs have various machine learning applications such as probabilistic modeling, generative modeling, and representation learning. However, their attractive properties often come at the cost of restricting the layer designs, which poses a question on their representation power: can we use these models to approximate sufficiently diverse functions? To answer this question, we have developed a general theoretical framework to investigate the representation power of INNs, building on a structure theorem of differential geometry. The framework simplifies the approximation problem of diffeomorphisms, which enables us to show the universal approximation properties of INNs. We apply the framework to two representative classes of INNs, namely Coupling-Flow-based INNs (CF-INNs) and Neural Ordinary Differential Equations (NODEs), and elucidate their high representation power despite the restrictions on their architectures.

Fast Estimation Method for the Stability of Ensemble Feature Selectors

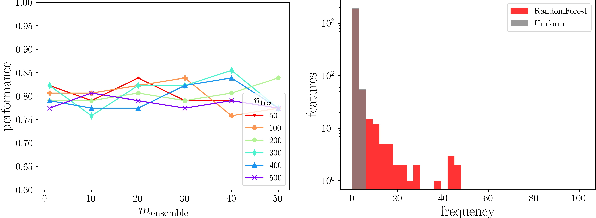
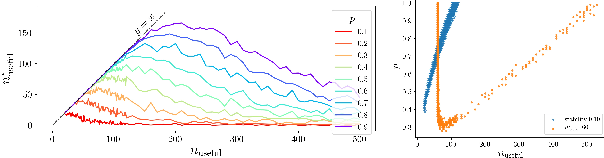
It is preferred that feature selectors be \textit{stable} for better interpretabity and robust prediction. Ensembling is known to be effective for improving the stability of feature selectors. Since ensembling is time-consuming, it is desirable to reduce the computational cost to estimate the stability of the ensemble feature selectors. We propose a simulator of a feature selector, and apply it to a fast estimation of the stability of ensemble feature selectors. To the best of our knowledge, this is the first study that estimates the stability of ensemble feature selectors and reduces the computation time theoretically and empirically.

Universal Approximation Property of Neural Ordinary Differential Equations

Neural ordinary differential equations (NODEs) is an invertible neural network architecture promising for its free-form Jacobian and the availability of a tractable Jacobian determinant estimator. Recently, the representation power of NODEs has been partly uncovered: they form an $L^p$-universal approximator for continuous maps under certain conditions. However, the $L^p$-universality may fail to guarantee an approximation for the entire input domain as it may still hold even if the approximator largely differs from the target function on a small region of the input space. To further uncover the potential of NODEs, we show their stronger approximation property, namely the $\sup$-universality for approximating a large class of diffeomorphisms. It is shown by leveraging a structure theorem of the diffeomorphism group, and the result complements the existing literature by establishing a fairly large set of mappings that NODEs can approximate with a stronger guarantee.

Coupling-based Invertible Neural Networks Are Universal Diffeomorphism Approximators

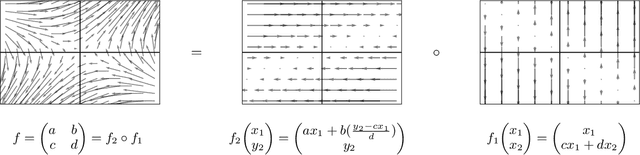
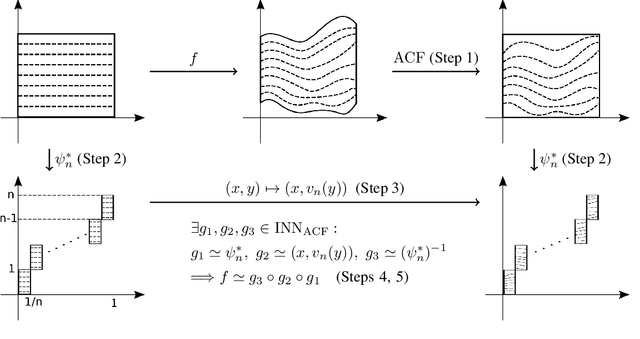
Invertible neural networks based on coupling flows (CF-INNs) have various machine learning applications such as image synthesis and representation learning. However, their desirable characteristics such as analytic invertibility come at the cost of restricting the functional forms. This poses a question on their representation power: are CF-INNs universal approximators for invertible functions? Without a universality, there could be a well-behaved invertible transformation that the CF-INN can never approximate, hence it would render the model class unreliable. We answer this question by showing a convenient criterion: a CF-INN is universal if its layers contain affine coupling and invertible linear functions as special cases. As its corollary, we can affirmatively resolve a previously unsolved problem: whether normalizing flow models based on affine coupling can be universal distributional approximators. In the course of proving the universality, we prove a general theorem to show the equivalence of the universality for certain diffeomorphism classes, a theoretical insight that is of interest by itself.

Optimization and Generalization Analysis of Transduction through Gradient Boosting and Application to Multi-scale Graph Neural Networks

It is known that the current graph neural networks (GNNs) are difficult to make themselves deep due to the problem known as \textit{over-smoothing}. Multi-scale GNNs are a promising approach for mitigating the over-smoothing problem. However, there is little explanation of why it works empirically from the viewpoint of learning theory. In this study, we derive the optimization and generalization guarantees of transductive learning algorithms that include multi-scale GNNs. Using the boosting theory, we prove the convergence of the training error under weak learning-type conditions. By combining it with generalization gap bounds in terms of transductive Rademacher complexity, we show that a test error bound of a specific type of multi-scale GNNs that decreases corresponding to the depth under the conditions. Our results offer theoretical explanations for the effectiveness of the multi-scale structure against the over-smoothing problem. We apply boosting algorithms to the training of multi-scale GNNs for real-world node prediction tasks. We confirm that its performance is comparable to existing GNNs, and the practical behaviors are consistent with theoretical observations. Code is available at https://github.com/delta2323/GB-GNN

Weisfeiler-Lehman Embedding for Molecular Graph Neural Networks

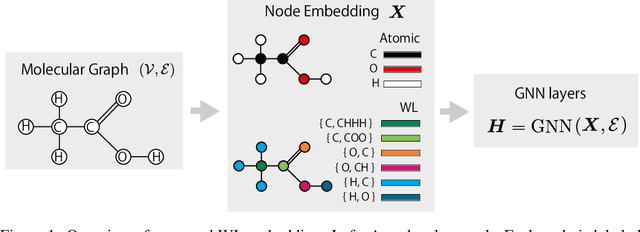
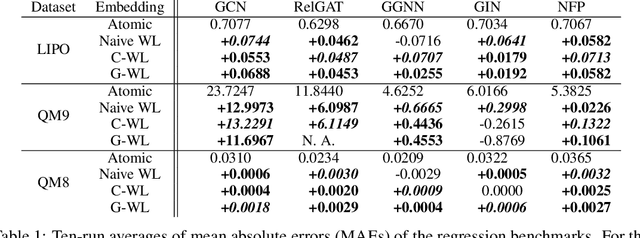
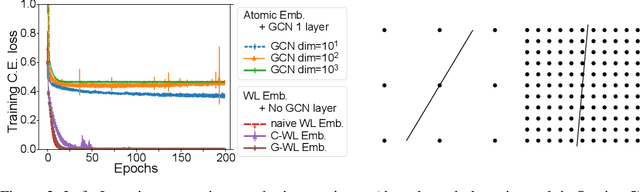
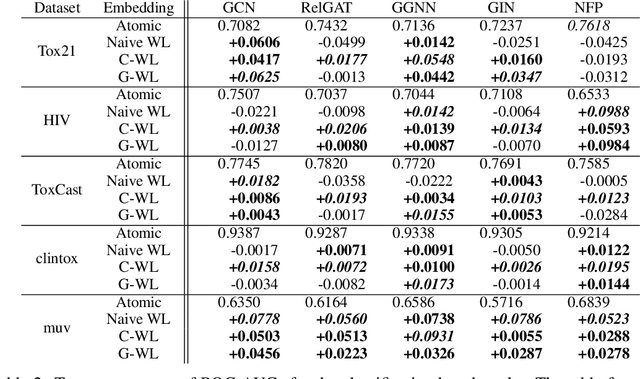
A graph neural network (GNN) is a good choice for predicting the chemical properties of molecules. Compared with other deep networks, however, the current performance of a GNN is limited owing to the "curse of depth." Inspired by long-established feature engineering in the field of chemistry, we expanded an atom representation using Weisfeiler-Lehman (WL) embedding, which is designed to capture local atomic patterns dominating the chemical properties of a molecule. In terms of representability, we show WL embedding can replace the first two layers of ReLU GNN -- a normal embedding and a hidden GNN layer -- with a smaller weight norm. We then demonstrate that WL embedding consistently improves the empirical performance over multiple GNN architectures and several molecular graph datasets.

Graph Residual Flow for Molecular Graph Generation

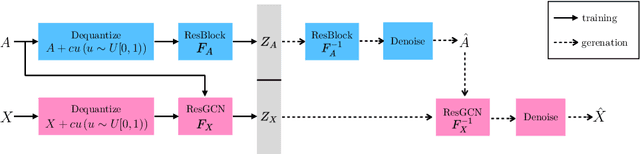
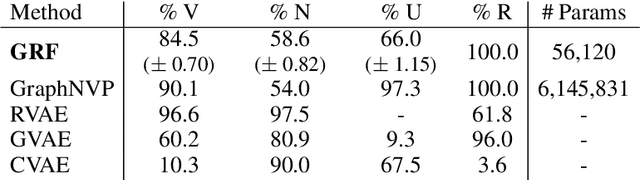
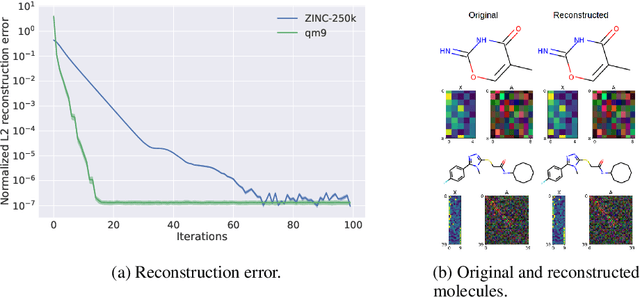
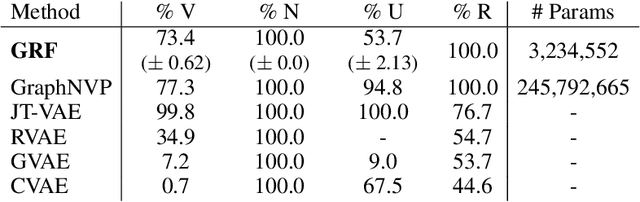
Statistical generative models for molecular graphs attract attention from many researchers from the fields of bio- and chemo-informatics. Among these models, invertible flow-based approaches are not fully explored yet. In this paper, we propose a powerful invertible flow for molecular graphs, called graph residual flow (GRF). The GRF is based on residual flows, which are known for more flexible and complex non-linear mappings than traditional coupling flows. We theoretically derive non-trivial conditions such that GRF is invertible, and present a way of keeping the entire flows invertible throughout the training and sampling. Experimental results show that a generative model based on the proposed GRF achieves comparable generation performance, with much smaller number of trainable parameters compared to the existing flow-based model.