Kohei Hayashi
Nara Institute of Science and Technology
JFlow: Model-Independent Spherical Jeans Analysis using Equivariant Continuous Normalizing Flows
May 01, 2025Abstract:The kinematics of stars in dwarf spheroidal galaxies have been studied to understand the structure of dark matter halos. However, the kinematic information of these stars is often limited to celestial positions and line-of-sight velocities, making full phase space analysis challenging. Conventional methods rely on projected analytic phase space density models with several parameters and infer dark matter halo structures by solving the spherical Jeans equation. In this paper, we introduce an unsupervised machine learning method for solving the spherical Jeans equation in a model-independent way as a first step toward model-independent analysis of dwarf spheroidal galaxies. Using equivariant continuous normalizing flows, we demonstrate that spherically symmetric stellar phase space densities and velocity dispersions can be estimated without model assumptions. As a proof of concept, we apply our method to Gaia challenge datasets for spherical models and measure dark matter mass densities given velocity anisotropy profiles. Our method can identify halo structures accurately, even with a small number of tracer stars.
When Does Metadata Conditioning (NOT) Work for Language Model Pre-Training? A Study with Context-Free Grammars
Apr 24, 2025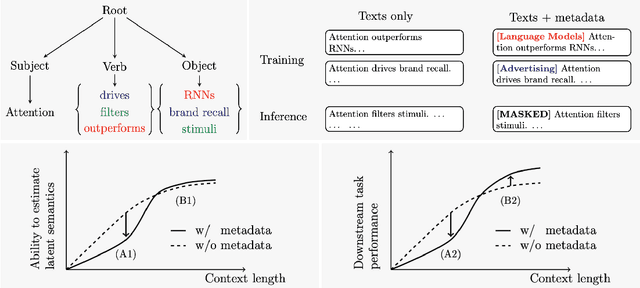
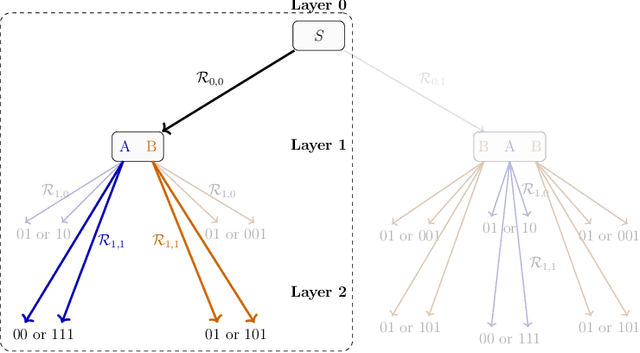
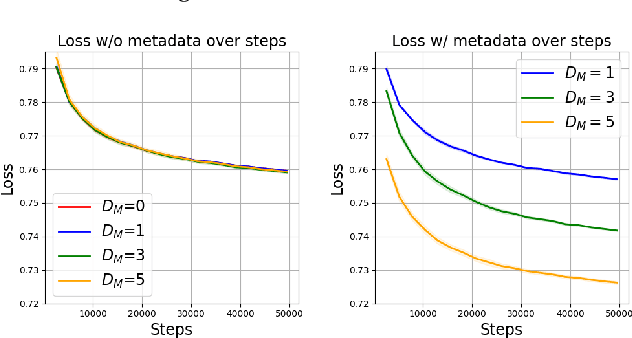

Abstract:The ability to acquire latent semantics is one of the key properties that determines the performance of language models. One convenient approach to invoke this ability is to prepend metadata (e.g. URLs, domains, and styles) at the beginning of texts in the pre-training data, making it easier for the model to access latent semantics before observing the entire text. Previous studies have reported that this technique actually improves the performance of trained models in downstream tasks; however, this improvement has been observed only in specific downstream tasks, without consistent enhancement in average next-token prediction loss. To understand this phenomenon, we closely investigate how prepending metadata during pre-training affects model performance by examining its behavior using artificial data. Interestingly, we found that this approach produces both positive and negative effects on the downstream tasks. We demonstrate that the effectiveness of the approach depends on whether latent semantics can be inferred from the downstream task's prompt. Specifically, through investigations using data generated by probabilistic context-free grammars, we show that training with metadata helps improve model's performance when the given context is long enough to infer the latent semantics. In contrast, the technique negatively impacts performance when the context lacks the necessary information to make an accurate posterior inference.
Simultaneous Learning of Optimal Transports for Training All-to-All Flow-Based Condition Transfer Model
Apr 04, 2025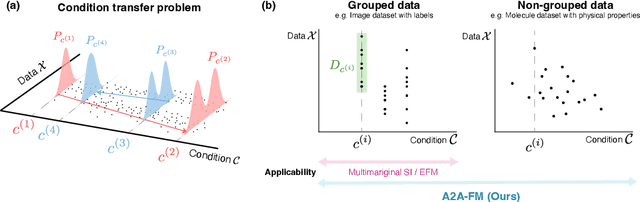

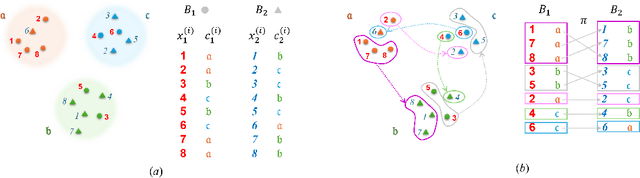

Abstract:In this paper, we propose a flow-based method for learning all-to-all transfer maps among conditional distributions, approximating pairwise optimal transport. The proposed method addresses the challenge of handling continuous conditions, which often involve a large set of conditions with sparse empirical observations per condition. We introduce a novel cost function that enables simultaneous learning of optimal transports for all pairs of conditional distributions. Our method is supported by a theoretical guarantee that, in the limit, it converges to pairwise optimal transports among infinite pairs of conditional distributions. The learned transport maps are subsequently used to couple data points in conditional flow matching. We demonstrate the effectiveness of this method on synthetic and benchmark datasets, as well as on chemical datasets where continuous physical properties are defined as conditions.
Inter-environmental world modeling for continuous and compositional dynamics
Mar 13, 2025Abstract:Various world model frameworks are being developed today based on autoregressive frameworks that rely on discrete representations of actions and observations, and these frameworks are succeeding in constructing interactive generative models for the target environment of interest. Meanwhile, humans demonstrate remarkable generalization abilities to combine experiences in multiple environments to mentally simulate and learn to control agents in diverse environments. Inspired by this human capability, we introduce World modeling through Lie Action (WLA), an unsupervised framework that learns continuous latent action representations to simulate across environments. WLA learns a control interface with high controllability and predictive ability by simultaneously modeling the dynamics of multiple environments using Lie group theory and object-centric autoencoder. On synthetic benchmark and real-world datasets, we demonstrate that WLA can be trained using only video frames and, with minimal or no action labels, can quickly adapt to new environments with novel action sets.
Extended Flow Matching: a Method of Conditional Generation with Generalized Continuity Equation
Mar 03, 2024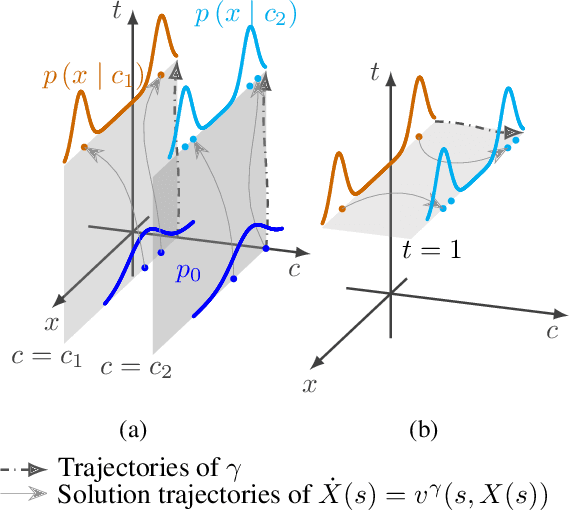
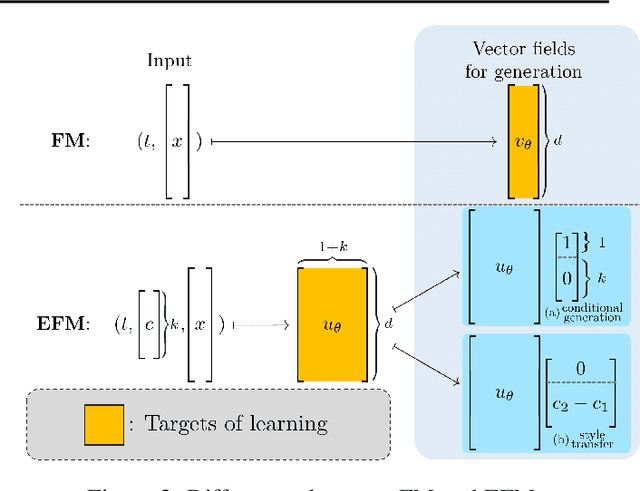
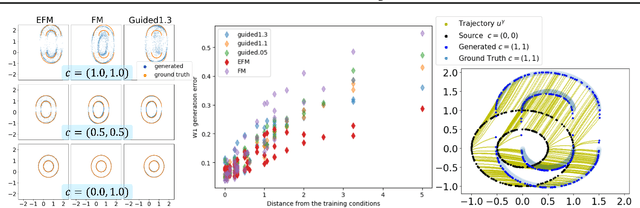
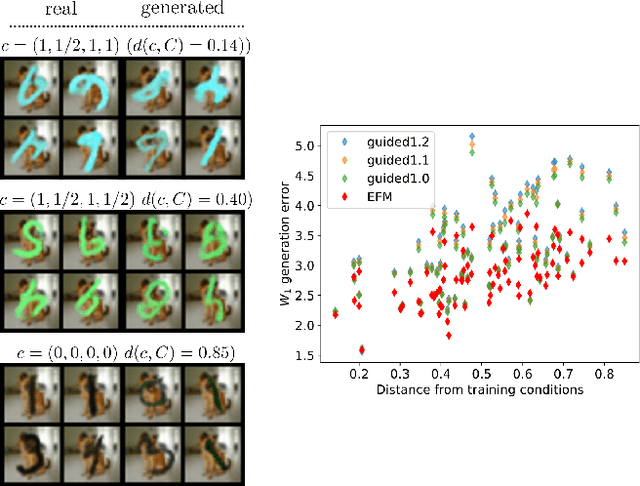
Abstract:The task of conditional generation is one of the most important applications of generative models, and numerous methods have been developed to date based on the celebrated diffusion models, with the guidance-based classifier-free method taking the lead. However, the theory of the guidance-based method not only requires the user to fine-tune the "guidance strength," but its target vector field does not necessarily correspond to the conditional distribution used in training. In this paper, we develop the theory of conditional generation based on Flow Matching, a current strong contender of diffusion methods. Motivated by the interpretation of a probability path as a distribution on path space, we establish a novel theory of flow-based generation of conditional distribution by employing the mathematical framework of generalized continuity equation instead of the continuity equation in flow matching. This theory naturally derives a method that aims to match the matrix field as opposed to the vector field. Our framework ensures the continuity of the generated conditional distribution through the existence of flow between conditional distributions. We will present our theory through experiments and mathematical results.
CFTM: Continuous time fractional topic model
Feb 07, 2024Abstract:In this paper, we propose the Continuous Time Fractional Topic Model (cFTM), a new method for dynamic topic modeling. This approach incorporates fractional Brownian motion~(fBm) to effectively identify positive or negative correlations in topic and word distribution over time, revealing long-term dependency or roughness. Our theoretical analysis shows that the cFTM can capture these long-term dependency or roughness in both topic and word distributions, mirroring the main characteristics of fBm. Moreover, we prove that the parameter estimation process for the cFTM is on par with that of LDA, traditional topic models. To demonstrate the cFTM's property, we conduct empirical study using economic news articles. The results from these tests support the model's ability to identify and track long-term dependency or roughness in topics over time.
Virtual Human Generative Model: Masked Modeling Approach for Learning Human Characteristics
Jun 19, 2023



Abstract:Identifying the relationship between healthcare attributes, lifestyles, and personality is vital for understanding and improving physical and mental conditions. Machine learning approaches are promising for modeling their relationships and offering actionable suggestions. In this paper, we propose Virtual Human Generative Model (VHGM), a machine learning model for estimating attributes about healthcare, lifestyles, and personalities. VHGM is a deep generative model trained with masked modeling to learn the joint distribution of attributes conditioned on known ones. Using heterogeneous tabular datasets, VHGM learns more than 1,800 attributes efficiently. We numerically evaluate the performance of VHGM and its training techniques. As a proof-of-concept of VHGM, we present several applications demonstrating user scenarios, such as virtual measurements of healthcare attributes and hypothesis verifications of lifestyles.
Neural Fourier Transform: A General Approach to Equivariant Representation Learning
May 29, 2023
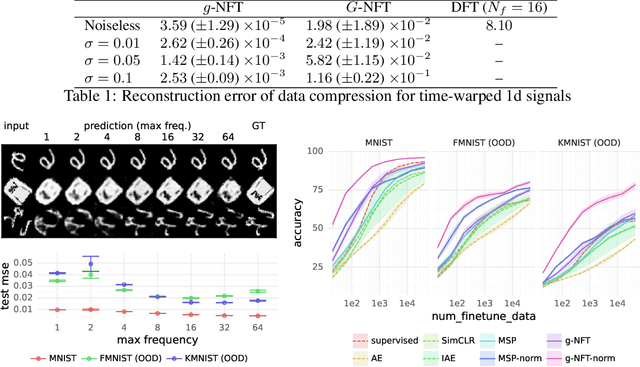
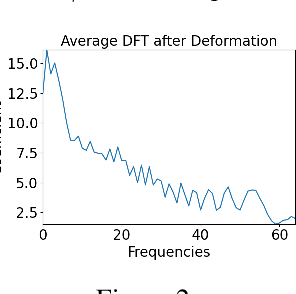

Abstract:Symmetry learning has proven to be an effective approach for extracting the hidden structure of data, with the concept of equivariance relation playing the central role. However, most of the current studies are built on architectural theory and corresponding assumptions on the form of data. We propose Neural Fourier Transform (NFT), a general framework of learning the latent linear action of the group without assuming explicit knowledge of how the group acts on data. We present the theoretical foundations of NFT and show that the existence of a linear equivariant feature, which has been assumed ubiquitously in equivariance learning, is equivalent to the existence of a group invariant kernel on the dataspace. We also provide experimental results to demonstrate the application of NFT in typical scenarios with varying levels of knowledge about the acting group.
TabRet: Pre-training Transformer-based Tabular Models for Unseen Columns
Apr 16, 2023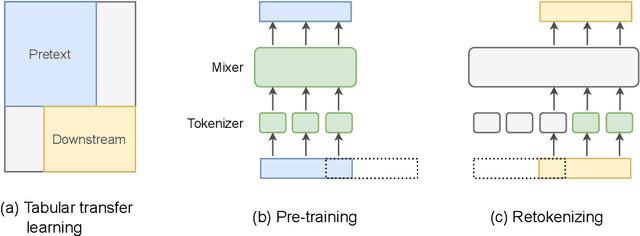
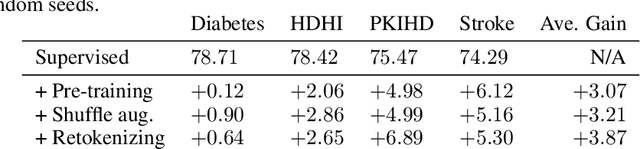
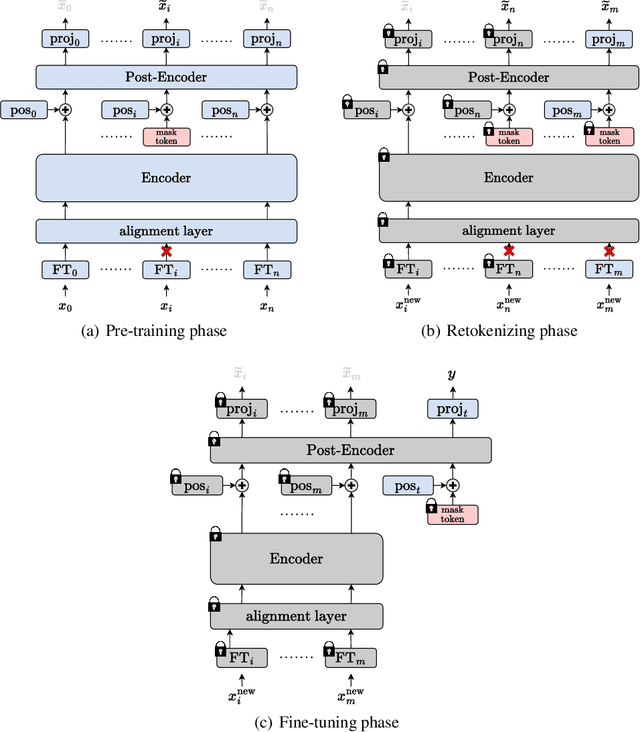
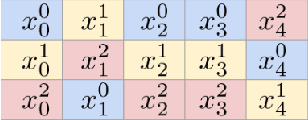
Abstract:We present \emph{TabRet}, a pre-trainable Transformer-based model for tabular data. TabRet is designed to work on a downstream task that contains columns not seen in pre-training. Unlike other methods, TabRet has an extra learning step before fine-tuning called \emph{retokenizing}, which calibrates feature embeddings based on the masked autoencoding loss. In experiments, we pre-trained TabRet with a large collection of public health surveys and fine-tuned it on classification tasks in healthcare, and TabRet achieved the best AUC performance on four datasets. In addition, an ablation study shows retokenizing and random shuffle augmentation of columns during pre-training contributed to performance gains. The code is available at https://github.com/pfnet-research/tabret .
Fractional SDE-Net: Generation of Time Series Data with Long-term Memory
Jan 16, 2022


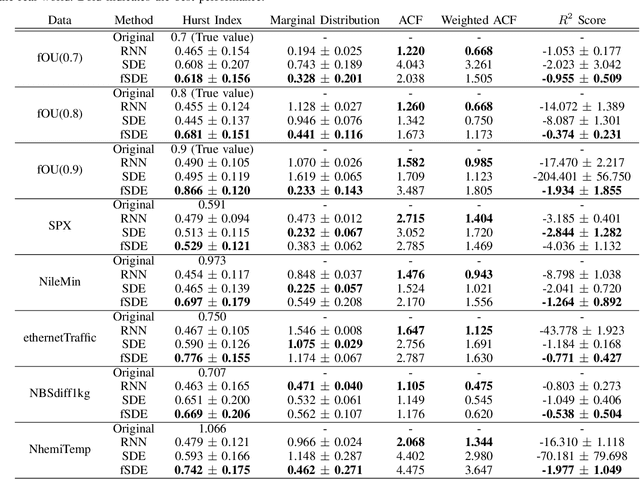
Abstract:In this paper, we focus on generation of time-series data using neural networks. It is often the case that input time-series data, especially taken from real financial markets, is irregularly sampled, and its noise structure is more complicated than i.i.d. type. To generate time series with such a property, we propose fSDE-Net: neural fractional Stochastic Differential Equation Network. It generalizes the neural SDE model by using fractional Brownian motion with Hurst index larger than half, which exhibits long-term memory property. We derive the solver of fSDE-Net and theoretically analyze the existence and uniqueness of the solution to fSDE-Net. Our experiments demonstrate that the fSDE-Net model can replicate distributional properties well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge