Naoki Nishikawa
From Shortcut to Induction Head: How Data Diversity Shapes Algorithm Selection in Transformers
Dec 21, 2025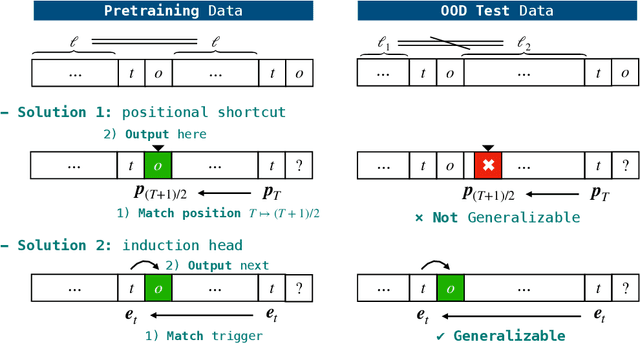
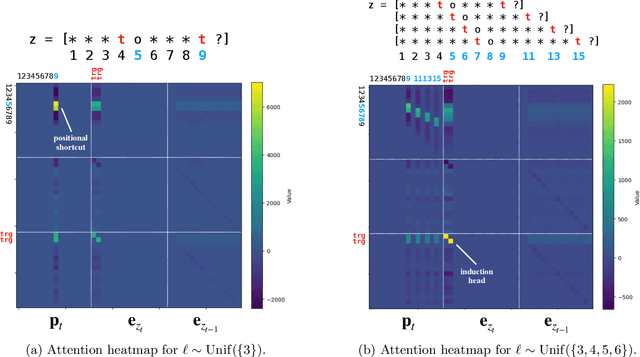
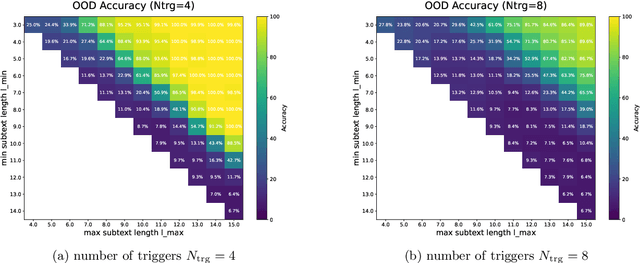
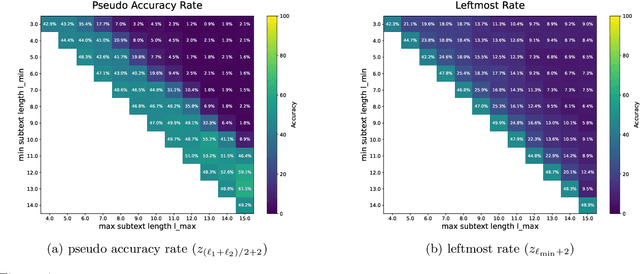
Abstract:Transformers can implement both generalizable algorithms (e.g., induction heads) and simple positional shortcuts (e.g., memorizing fixed output positions). In this work, we study how the choice of pretraining data distribution steers a shallow transformer toward one behavior or the other. Focusing on a minimal trigger-output prediction task -- copying the token immediately following a special trigger upon its second occurrence -- we present a rigorous analysis of gradient-based training of a single-layer transformer. In both the infinite and finite sample regimes, we prove a transition in the learned mechanism: if input sequences exhibit sufficient diversity, measured by a low ``max-sum'' ratio of trigger-to-trigger distances, the trained model implements an induction head and generalizes to unseen contexts; by contrast, when this ratio is large, the model resorts to a positional shortcut and fails to generalize out-of-distribution (OOD). We also reveal a trade-off between the pretraining context length and OOD generalization, and derive the optimal pretraining distribution that minimizes computational cost per sample. Finally, we validate our theoretical predictions with controlled synthetic experiments, demonstrating that broadening context distributions robustly induces induction heads and enables OOD generalization. Our results shed light on the algorithmic biases of pretrained transformers and offer conceptual guidelines for data-driven control of their learned behaviors.
When Does Metadata Conditioning (NOT) Work for Language Model Pre-Training? A Study with Context-Free Grammars
Apr 24, 2025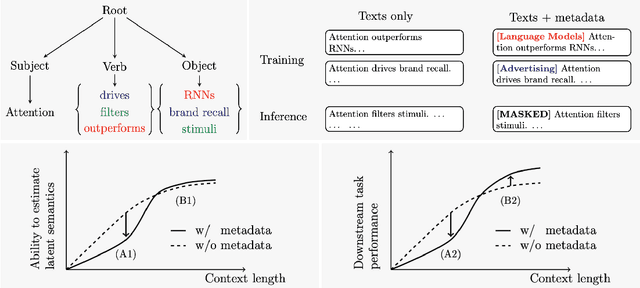
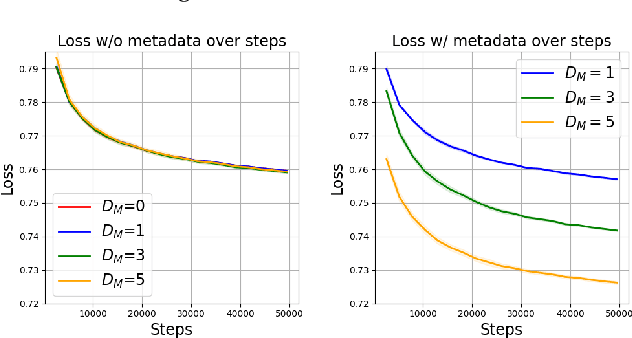

Abstract:The ability to acquire latent semantics is one of the key properties that determines the performance of language models. One convenient approach to invoke this ability is to prepend metadata (e.g. URLs, domains, and styles) at the beginning of texts in the pre-training data, making it easier for the model to access latent semantics before observing the entire text. Previous studies have reported that this technique actually improves the performance of trained models in downstream tasks; however, this improvement has been observed only in specific downstream tasks, without consistent enhancement in average next-token prediction loss. To understand this phenomenon, we closely investigate how prepending metadata during pre-training affects model performance by examining its behavior using artificial data. Interestingly, we found that this approach produces both positive and negative effects on the downstream tasks. We demonstrate that the effectiveness of the approach depends on whether latent semantics can be inferred from the downstream task's prompt. Specifically, through investigations using data generated by probabilistic context-free grammars, we show that training with metadata helps improve model's performance when the given context is long enough to infer the latent semantics. In contrast, the technique negatively impacts performance when the context lacks the necessary information to make an accurate posterior inference.
State Space Models are Comparable to Transformers in Estimating Functions with Dynamic Smoothness
May 29, 2024Abstract:Deep neural networks based on state space models (SSMs) are attracting much attention in sequence modeling since their computational cost is significantly smaller than that of Transformers. While the capabilities of SSMs have been primarily investigated through experimental comparisons, theoretical understanding of SSMs is still limited. In particular, there is a lack of statistical and quantitative evaluation of whether SSM can replace Transformers. In this paper, we theoretically explore in which tasks SSMs can be alternatives of Transformers from the perspective of estimating sequence-to-sequence functions. We consider the setting where the target function has direction-dependent smoothness and prove that SSMs can estimate such functions with the same convergence rate as Transformers. Additionally, we prove that SSMs can estimate the target function, even if the smoothness changes depending on the input sequence, as well as Transformers. Our results show the possibility that SSMs can replace Transformers when estimating the functions in certain classes that appear in practice.
Adaptive Topological Feature via Persistent Homology: Filtration Learning for Point Clouds
Jul 18, 2023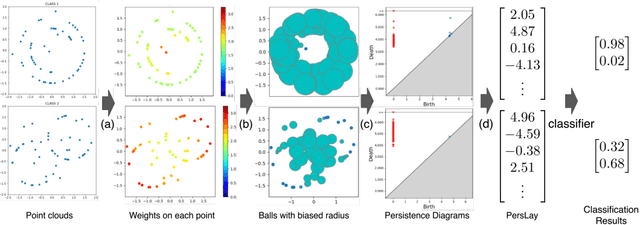
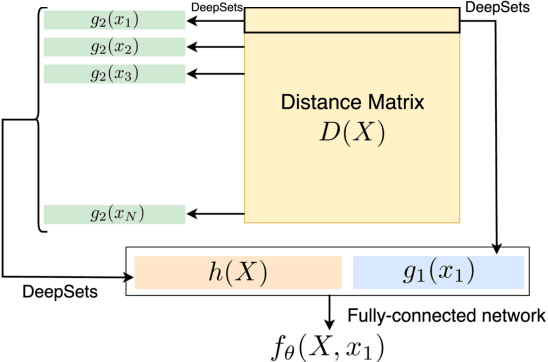
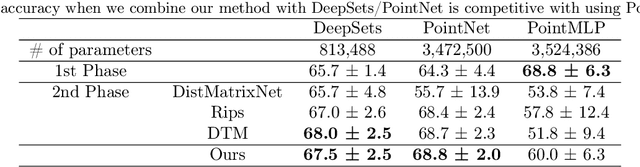
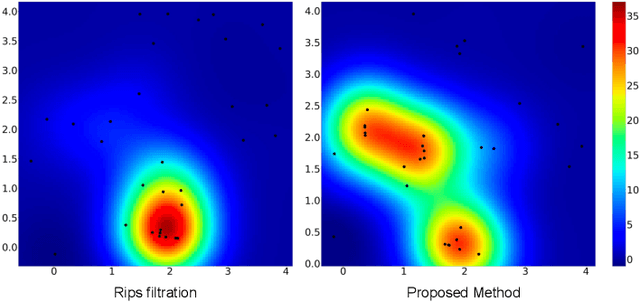
Abstract:Machine learning for point clouds has been attracting much attention, with many applications in various fields, such as shape recognition and material science. To enhance the accuracy of such machine learning methods, it is known to be effective to incorporate global topological features, which are typically extracted by persistent homology. In the calculation of persistent homology for a point cloud, we need to choose a filtration for the point clouds, an increasing sequence of spaces. Because the performance of machine learning methods combined with persistent homology is highly affected by the choice of a filtration, we need to tune it depending on data and tasks. In this paper, we propose a framework that learns a filtration adaptively with the use of neural networks. In order to make the resulting persistent homology isometry-invariant, we develop a neural network architecture with such invariance. Additionally, we theoretically show a finite-dimensional approximation result that justifies our architecture. Experimental results demonstrated the efficacy of our framework in several classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge