Graph Community Augmentation with GMM-based Modeling in Latent Space

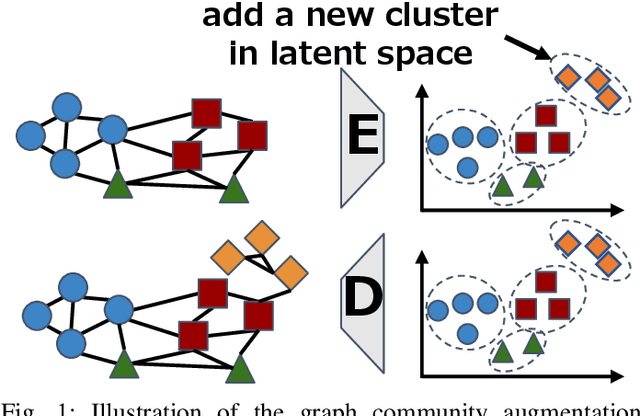
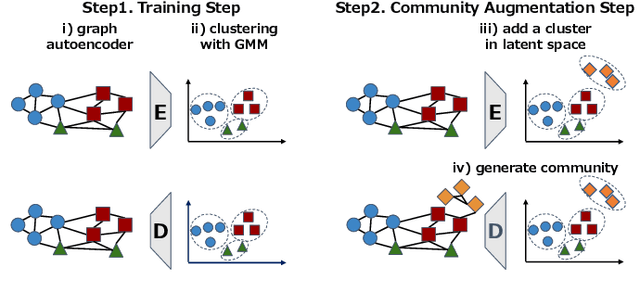
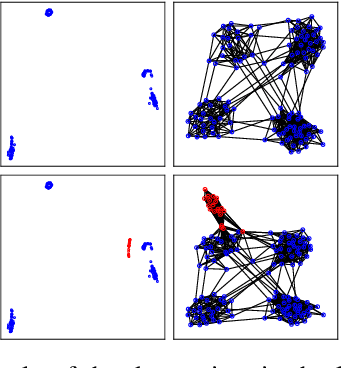
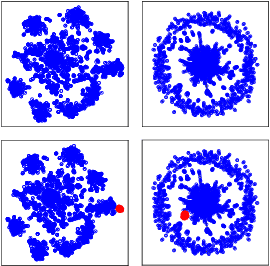
This study addresses the issue of graph generation with generative models. In particular, we are concerned with graph community augmentation problem, which refers to the problem of generating unseen or unfamiliar graphs with a new community out of the probability distribution estimated with a given graph dataset. The graph community augmentation means that the generated graphs have a new community. There is a chance of discovering an unseen but important structure of graphs with a new community, for example, in a social network such as a purchaser network. Graph community augmentation may also be helpful for generalization of data mining models in a case where it is difficult to collect real graph data enough. In fact, there are many ways to generate a new community in an existing graph. It is desirable to discover a new graph with a new community beyond the given graph while we keep the structure of the original graphs to some extent for the generated graphs to be realistic. To this end, we propose an algorithm called the graph community augmentation (GCA). The key ideas of GCA are (i) to fit Gaussian mixture model (GMM) to data points in the latent space into which the nodes in the original graph are embedded, and (ii) to add data points in the new cluster in the latent space for generating a new community based on the minimum description length (MDL) principle. We empirically demonstrate the effectiveness of GCA for generating graphs with a new community structure on synthetic and real datasets.

Foundation of Calculating Normalized Maximum Likelihood for Continuous Probability Models

The normalized maximum likelihood (NML) code length is widely used as a model selection criterion based on the minimum description length principle, where the model with the shortest NML code length is selected. A common method to calculate the NML code length is to use the sum (for a discrete model) or integral (for a continuous model) of a function defined by the distribution of the maximum likelihood estimator. While this method has been proven to correctly calculate the NML code length of discrete models, no proof has been provided for continuous cases. Consequently, it has remained unclear whether the method can accurately calculate the NML code length of continuous models. In this paper, we solve this problem affirmatively, proving that the method is also correct for continuous cases. Remarkably, completing the proof for continuous cases is non-trivial in that it cannot be achieved by merely replacing the sums in discrete cases with integrals, as the decomposition trick applied to sums in the discrete model case proof is not applicable to integrals in the continuous model case proof. To overcome this, we introduce a novel decomposition approach based on the coarea formula from geometric measure theory, which is essential to establishing our proof for continuous cases.

Clustering Change Sign Detection by Fusing Mixture Complexity

This paper proposes an early detection method for cluster structural changes. Cluster structure refers to discrete structural characteristics, such as the number of clusters, when data are represented using finite mixture models, such as Gaussian mixture models. We focused on scenarios in which the cluster structure gradually changed over time. For finite mixture models, the concept of mixture complexity (MC) measures the continuous cluster size by considering the cluster proportion bias and overlap between clusters. In this paper, we propose MC fusion as an extension of MC to handle situations in which multiple mixture numbers are possible in a finite mixture model. By incorporating the fusion of multiple models, our approach accurately captured the cluster structure during transitional periods of gradual change. Moreover, we introduce a method for detecting changes in the cluster structure by examining the transition of MC fusion. We demonstrate the effectiveness of our method through empirical analysis using both artificial and real-world datasets.

Balancing Summarization and Change Detection in Graph Streams

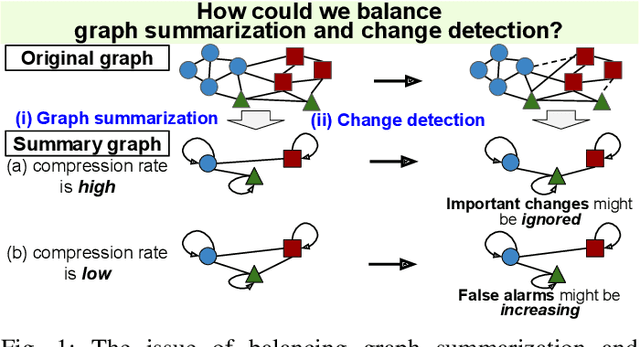
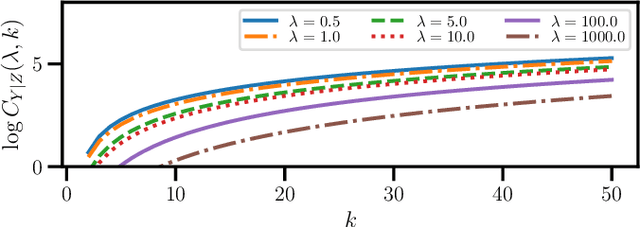
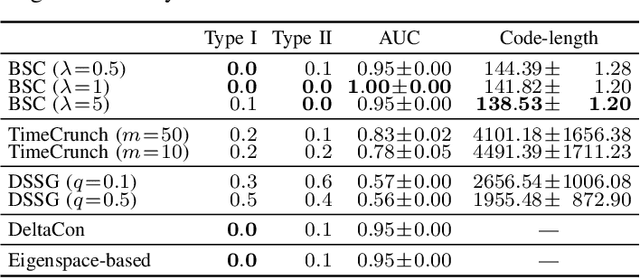
This study addresses the issue of balancing graph summarization and graph change detection. Graph summarization compresses large-scale graphs into a smaller scale. However, the question remains: To what extent should the original graph be compressed? This problem is solved from the perspective of graph change detection, aiming to detect statistically significant changes using a stream of summary graphs. If the compression rate is extremely high, important changes can be ignored, whereas if the compression rate is extremely low, false alarms may increase with more memory. This implies that there is a trade-off between compression rate in graph summarization and accuracy in change detection. We propose a novel quantitative methodology to balance this trade-off to simultaneously realize reliable graph summarization and change detection. We introduce a probabilistic structure of hierarchical latent variable model into a graph, thereby designing a parameterized summary graph on the basis of the minimum description length principle. The parameter specifying the summary graph is then optimized so that the accuracy of change detection is guaranteed to suppress Type I error probability (probability of raising false alarms) to be less than a given confidence level. First, we provide a theoretical framework for connecting graph summarization with change detection. Then, we empirically demonstrate its effectiveness on synthetic and real datasets.

Adaptive Topological Feature via Persistent Homology: Filtration Learning for Point Clouds

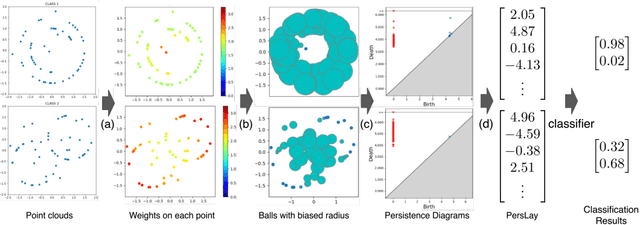
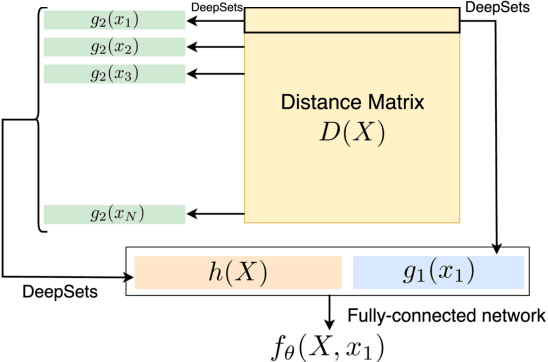
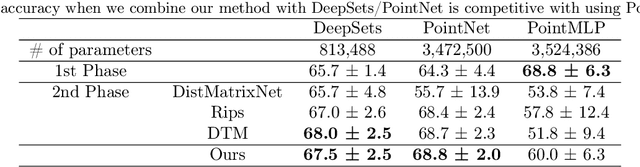
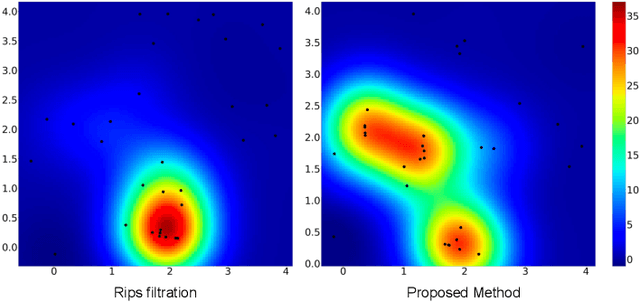
Machine learning for point clouds has been attracting much attention, with many applications in various fields, such as shape recognition and material science. To enhance the accuracy of such machine learning methods, it is known to be effective to incorporate global topological features, which are typically extracted by persistent homology. In the calculation of persistent homology for a point cloud, we need to choose a filtration for the point clouds, an increasing sequence of spaces. Because the performance of machine learning methods combined with persistent homology is highly affected by the choice of a filtration, we need to tune it depending on data and tasks. In this paper, we propose a framework that learns a filtration adaptively with the use of neural networks. In order to make the resulting persistent homology isometry-invariant, we develop a neural network architecture with such invariance. Additionally, we theoretically show a finite-dimensional approximation result that justifies our architecture. Experimental results demonstrated the efficacy of our framework in several classification tasks.

Tight and fast generalization error bound of graph embedding in metric space

Recent studies have experimentally shown that we can achieve in non-Euclidean metric space effective and efficient graph embedding, which aims to obtain the vertices' representations reflecting the graph's structure in the metric space. Specifically, graph embedding in hyperbolic space has experimentally succeeded in embedding graphs with hierarchical-tree structure, e.g., data in natural languages, social networks, and knowledge bases. However, recent theoretical analyses have shown a much higher upper bound on non-Euclidean graph embedding's generalization error than Euclidean one's, where a high generalization error indicates that the incompleteness and noise in the data can significantly damage learning performance. It implies that the existing bound cannot guarantee the success of graph embedding in non-Euclidean metric space in a practical training data size, which can prevent non-Euclidean graph embedding's application in real problems. This paper provides a novel upper bound of graph embedding's generalization error by evaluating the local Rademacher complexity of the model as a function set of the distances of representation couples. Our bound clarifies that the performance of graph embedding in non-Euclidean metric space, including hyperbolic space, is better than the existing upper bounds suggest. Specifically, our new upper bound is polynomial in the metric space's geometric radius $R$ and can be $O(\frac{1}{S})$ at the fastest, where $S$ is the training data size. Our bound is significantly tighter and faster than the existing one, which can be exponential to $R$ and $O(\frac{1}{\sqrt{S}})$ at the fastest. Specific calculations on example cases show that graph embedding in non-Euclidean metric space can outperform that in Euclidean space with much smaller training data than the existing bound has suggested.

Detecting Signs of Model Change with Continuous Model Selection Based on Descriptive Dimensionality

We address the issue of detecting changes of models that lie behind a data stream. The model refers to an integer-valued structural information such as the number of free parameters in a parametric model. Specifically we are concerned with the problem of how we can detect signs of model changes earlier than they are actualized. To this end, we employ {\em continuous model selection} on the basis of the notion of {\em descriptive dimensionality}~(Ddim). It is a real-valued model dimensionality, which is designed for quantifying the model dimensionality in the model transition period. Continuous model selection is to determine the real-valued model dimensionality in terms of Ddim from a given data. We propose a novel methodology for detecting signs of model changes by tracking the rise-up of Ddim in a data stream. We apply this methodology to detecting signs of changes of the number of clusters in a Gaussian mixture model and those of the order in an auto regression model. With synthetic and real data sets, we empirically demonstrate its effectiveness by showing that it is able to visualize well how rapidly model dimensionality moves in the transition period and to raise early warning signals of model changes earlier than they are detected with existing methods.

Generalization Error Bound for Hyperbolic Ordinal Embedding

Hyperbolic ordinal embedding (HOE) represents entities as points in hyperbolic space so that they agree as well as possible with given constraints in the form of entity i is more similar to entity j than to entity k. It has been experimentally shown that HOE can obtain representations of hierarchical data such as a knowledge base and a citation network effectively, owing to hyperbolic space's exponential growth property. However, its theoretical analysis has been limited to ideal noiseless settings, and its generalization error in compensation for hyperbolic space's exponential representation ability has not been guaranteed. The difficulty is that existing generalization error bound derivations for ordinal embedding based on the Gramian matrix do not work in HOE, since hyperbolic space is not inner-product space. In this paper, through our novel characterization of HOE with decomposed Lorentz Gramian matrices, we provide a generalization error bound of HOE for the first time, which is at most exponential with respect to the embedding space's radius. Our comparison between the bounds of HOE and Euclidean ordinal embedding shows that HOE's generalization error is reasonable as a cost for its exponential representation ability.

Detecting Hierarchical Changes in Latent Variable Models

This paper addresses the issue of detecting hierarchical changes in latent variable models (HCDL) from data streams. There are three different levels of changes for latent variable models: 1) the first level is the change in data distribution for fixed latent variables, 2) the second one is that in the distribution over latent variables, and 3) the third one is that in the number of latent variables. It is important to detect these changes because we can analyze the causes of changes by identifying which level a change comes from (change interpretability). This paper proposes an information-theoretic framework for detecting changes of the three levels in a hierarchical way. The key idea to realize it is to employ the MDL (minimum description length) change statistics for measuring the degree of change, in combination with DNML (decomposed normalized maximum likelihood) code-length calculation. We give a theoretical basis for making reliable alarms for changes. Focusing on stochastic block models, we employ synthetic and benchmark datasets to empirically demonstrate the effectiveness of our framework in terms of change interpretability as well as change detection.

Word2vec Skip-gram Dimensionality Selection via Sequential Normalized Maximum Likelihood

In this paper, we propose a novel information criteria-based approach to select the dimensionality of the word2vec Skip-gram (SG). From the perspective of the probability theory, SG is considered as an implicit probability distribution estimation under the assumption that there exists a true contextual distribution among words. Therefore, we apply information criteria with the aim of selecting the best dimensionality so that the corresponding model can be as close as possible to the true distribution. We examine the following information criteria for the dimensionality selection problem: the Akaike Information Criterion, Bayesian Information Criterion, and Sequential Normalized Maximum Likelihood (SNML) criterion. SNML is the total codelength required for the sequential encoding of a data sequence on the basis of the minimum description length. The proposed approach is applied to both the original SG model and the SG Negative Sampling model to clarify the idea of using information criteria. Additionally, as the original SNML suffers from computational disadvantages, we introduce novel heuristics for its efficient computation. Moreover, we empirically demonstrate that SNML outperforms both BIC and AIC. In comparison with other evaluation methods for word embedding, the dimensionality selected by SNML is significantly closer to the optimal dimensionality obtained by word analogy or word similarity tasks.