Detecting Signs of Model Change with Continuous Model Selection Based on Descriptive Dimensionality

We address the issue of detecting changes of models that lie behind a data stream. The model refers to an integer-valued structural information such as the number of free parameters in a parametric model. Specifically we are concerned with the problem of how we can detect signs of model changes earlier than they are actualized. To this end, we employ {\em continuous model selection} on the basis of the notion of {\em descriptive dimensionality}~(Ddim). It is a real-valued model dimensionality, which is designed for quantifying the model dimensionality in the model transition period. Continuous model selection is to determine the real-valued model dimensionality in terms of Ddim from a given data. We propose a novel methodology for detecting signs of model changes by tracking the rise-up of Ddim in a data stream. We apply this methodology to detecting signs of changes of the number of clusters in a Gaussian mixture model and those of the order in an auto regression model. With synthetic and real data sets, we empirically demonstrate its effectiveness by showing that it is able to visualize well how rapidly model dimensionality moves in the transition period and to raise early warning signals of model changes earlier than they are detected with existing methods.

Spectral-Pruning: Compressing deep neural network via spectral analysis

The model size of deep neural network is getting larger and larger to realize superior performance in complicated tasks. This makes it difficult to implement deep neural network in small edge-computing devices. To overcome this problem, model compression methods have been gathering much attention. However, there have been only few theoretical back-grounds that explain what kind of quantity determines the compression ability. To resolve this issue, we develop a new theoretical frame-work for model compression, and propose a new method called {\it Spectral-Pruning} based on the theory. Our theoretical analysis is based on the observation such that the eigenvalues of the covariance matrix of the output from nodes in the internal layers often shows rapid decay. We define "degree of freedom" to quantify an intrinsic dimensionality of the model by using the eigenvalue distribution and show that the compression ability is essentially controlled by this quantity. Along with this, we give a generalization error bound of the compressed model. Our proposed method is applicable to wide range of models, unlike the existing methods, e.g., ones possess complicated branches as implemented in SegNet and ResNet. Our method makes use of both "input" and "output" in each layer and is easy to implement. We apply our method to several datasets to justify our theoretical analyses and show that the proposed method achieves the state-of-the-art performance.

Normalized Maximum Likelihood Coding for Exponential Family with Its Applications to Optimal Clustering

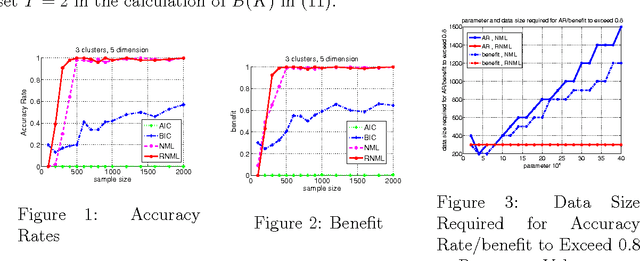
We are concerned with the issue of how to calculate the normalized maximum likelihood (NML) code-length. There is a problem that the normalization term of the NML code-length may diverge when it is continuous and unbounded and a straightforward computation of it is highly expensive when the data domain is finite . In previous works it has been investigated how to calculate the NML code-length for specific types of distributions. We first propose a general method for computing the NML code-length for the exponential family. Then we specifically focus on Gaussian mixture model (GMM), and propose a new efficient method for computing the NML to them. We develop it by generalizing Rissanen's re-normalizing technique. Then we apply this method to the clustering issue, in which a clustering structure is modeled using a GMM, and the main task is to estimate the optimal number of clusters on the basis of the NML code-length. We demonstrate using artificial data sets the superiority of the NML-based clustering over other criteria such as AIC, BIC in terms of the data size required for high accuracy rate to be achieved.