DIFF2: Differential Private Optimization via Gradient Differences for Nonconvex Distributed Learning

Differential private optimization for nonconvex smooth objective is considered. In the previous work, the best known utility bound is $\widetilde O(\sqrt{d}/(n\varepsilon_\mathrm{DP}))$ in terms of the squared full gradient norm, which is achieved by Differential Private Gradient Descent (DP-GD) as an instance, where $n$ is the sample size, $d$ is the problem dimensionality and $\varepsilon_\mathrm{DP}$ is the differential privacy parameter. To improve the best known utility bound, we propose a new differential private optimization framework called \emph{DIFF2 (DIFFerential private optimization via gradient DIFFerences)} that constructs a differential private global gradient estimator with possibly quite small variance based on communicated \emph{gradient differences} rather than gradients themselves. It is shown that DIFF2 with a gradient descent subroutine achieves the utility of $\widetilde O(d^{2/3}/(n\varepsilon_\mathrm{DP})^{4/3})$, which can be significantly better than the previous one in terms of the dependence on the sample size $n$. To the best of our knowledge, this is the first fundamental result to improve the standard utility $\widetilde O(\sqrt{d}/(n\varepsilon_\mathrm{DP}))$ for nonconvex objectives. Additionally, a more computational and communication efficient subroutine is combined with DIFF2 and its theoretical analysis is also given. Numerical experiments are conducted to validate the superiority of DIFF2 framework.

Escaping Saddle Points with Bias-Variance Reduced Local Perturbed SGD for Communication Efficient Nonconvex Distributed Learning

In recent centralized nonconvex distributed learning and federated learning, local methods are one of the promising approaches to reduce communication time. However, existing work has mainly focused on studying first-order optimality guarantees. On the other side, second-order optimality guaranteed algorithms have been extensively studied in the non-distributed optimization literature. In this paper, we study a new local algorithm called Bias-Variance Reduced Local Perturbed SGD (BVR-L-PSGD), that combines the existing bias-variance reduced gradient estimator with parameter perturbation to find second-order optimal points in centralized nonconvex distributed optimization. BVR-L-PSGD enjoys second-order optimality with nearly the same communication complexity as the best known one of BVR-L-SGD to find first-order optimality. Particularly, the communication complexity is better than non-local methods when the local datasets heterogeneity is smaller than the smoothness of the local loss. In an extreme case, the communication complexity approaches to $\widetilde \Theta(1)$ when the local datasets heterogeneity goes to zero.

Bias-Variance Reduced Local SGD for Less Heterogeneous Federated Learning

Federated learning is one of the important learning scenarios in distributed learning, in which we aim at learning heterogeneous local datasets efficiently in terms of communication and computational cost. In this paper, we study new local algorithms called Bias-Variance Reduced Local SGD (BVR-L-SGD) for nonconvex federated learning. One of the novelties of this paper is in the analysis of our bias and variance reduced local gradient estimators which fully utilize small second-order heterogeneity of local objectives and suggests to randomly pick up one of the local models instead of taking average of them when workers are synchronized. Under small heterogeneity of local objectives, we show that our methods achieve smaller communication complexity than both the previous non-local and local methods for general nonconvex objectives. Furthermore, we also compare the total execution time, that is the sum of total communication time and total computational time per worker, and show the superiority of our methods to the existing methods when the heterogeneity is small and single communication time is more time consuming than single stochastic gradient computation. Numerical results are provided to verify our theoretical findings and give empirical evidence of the superiority of our algorithms.

Gradient Descent in RKHS with Importance Labeling

Labeling cost is often expensive and is a fundamental limitation of supervised learning. In this paper, we study importance labeling problem, in which we are given many unlabeled data and select a limited number of data to be labeled from the unlabeled data, and then a learning algorithm is executed on the selected one. We propose a new importance labeling scheme and analyse the generalization error of gradient descent combined with our labeling scheme in least squares regression in Reproducing Kernel Hilbert Spaces (RKHS). We show that the proposed importance labeling leads to much better generalization ability than uniform one under near interpolation settings. Numerical experiments verify our theoretical findings.

Accelerated Sparsified SGD with Error Feedback

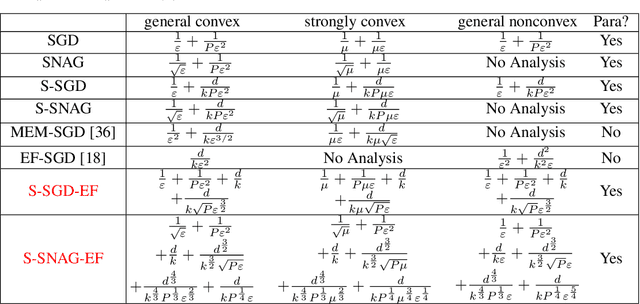
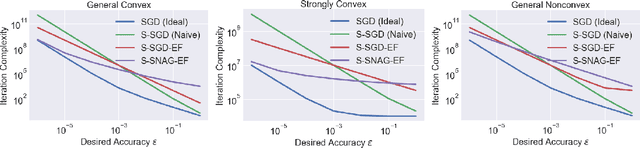
We study a stochastic gradient method for synchronous distributed optimization. For reducing communication cost, we are interested in utilizing compression of communicated gradients. Our main focus is a {\it{sparsified}} stochastic gradient method with {\it{error feedback}} scheme combined with {\it{Nesterov's acceleration}}. Strong theoretical analysis of sparsified SGD with error feedback in parallel computing settings and an application of acceleration scheme to sparsified SGD with error feedback are new. It is shown that (i) our method asymptotically achieves the same iteration complexity of non-sparsified SGD even in parallel computing settings; (ii) Nesterov's acceleration can improve the iteration complexity of non-accelerated methods in convex and even in nonconvex optimization problems for moderate optimization accuracy.

Sample Efficient Stochastic Gradient Iterative Hard Thresholding Method for Stochastic Sparse Linear Regression with Limited Attribute Observation

We develop new stochastic gradient methods for efficiently solving sparse linear regression in a partial attribute observation setting, where learners are only allowed to observe a fixed number of actively chosen attributes per example at training and prediction times. It is shown that the methods achieve essentially a sample complexity of $O(1/\varepsilon)$ to attain an error of $\varepsilon$ under a variant of restricted eigenvalue condition, and the rate has better dependency on the problem dimension than existing methods. Particularly, if the smallest magnitude of the non-zero components of the optimal solution is not too small, the rate of our proposed {\it Hybrid} algorithm can be boosted to near the minimax optimal sample complexity of {\it full information} algorithms. The core ideas are (i) efficient construction of an unbiased gradient estimator by the iterative usage of the hard thresholding operator for configuring an exploration algorithm; and (ii) an adaptive combination of the exploration and an exploitation algorithms for quickly identifying the support of the optimum and efficiently searching the optimal parameter in its support. Experimental results are presented to validate our theoretical findings and the superiority of our proposed methods.

Spectral-Pruning: Compressing deep neural network via spectral analysis

The model size of deep neural network is getting larger and larger to realize superior performance in complicated tasks. This makes it difficult to implement deep neural network in small edge-computing devices. To overcome this problem, model compression methods have been gathering much attention. However, there have been only few theoretical back-grounds that explain what kind of quantity determines the compression ability. To resolve this issue, we develop a new theoretical frame-work for model compression, and propose a new method called {\it Spectral-Pruning} based on the theory. Our theoretical analysis is based on the observation such that the eigenvalues of the covariance matrix of the output from nodes in the internal layers often shows rapid decay. We define "degree of freedom" to quantify an intrinsic dimensionality of the model by using the eigenvalue distribution and show that the compression ability is essentially controlled by this quantity. Along with this, we give a generalization error bound of the compressed model. Our proposed method is applicable to wide range of models, unlike the existing methods, e.g., ones possess complicated branches as implemented in SegNet and ResNet. Our method makes use of both "input" and "output" in each layer and is easy to implement. We apply our method to several datasets to justify our theoretical analyses and show that the proposed method achieves the state-of-the-art performance.

Doubly Accelerated Stochastic Variance Reduced Dual Averaging Method for Regularized Empirical Risk Minimization

In this paper, we develop a new accelerated stochastic gradient method for efficiently solving the convex regularized empirical risk minimization problem in mini-batch settings. The use of mini-batches is becoming a golden standard in the machine learning community, because mini-batch settings stabilize the gradient estimate and can easily make good use of parallel computing. The core of our proposed method is the incorporation of our new "double acceleration" technique and variance reduction technique. We theoretically analyze our proposed method and show that our method much improves the mini-batch efficiencies of previous accelerated stochastic methods, and essentially only needs size $\sqrt{n}$ mini-batches for achieving the optimal iteration complexities for both non-strongly and strongly convex objectives, where $n$ is the training set size. Further, we show that even in non-mini-batch settings, our method achieves the best known convergence rate for both non-strongly and strongly convex objectives.

Stochastic dual averaging methods using variance reduction techniques for regularized empirical risk minimization problems

We consider a composite convex minimization problem associated with regularized empirical risk minimization, which often arises in machine learning. We propose two new stochastic gradient methods that are based on stochastic dual averaging method with variance reduction. Our methods generate a sparser solution than the existing methods because we do not need to take the average of the history of the solutions. This is favorable in terms of both interpretability and generalization. Moreover, our methods have theoretical support for both a strongly and a non-strongly convex regularizer and achieve the best known convergence rates among existing nonaccelerated stochastic gradient methods.