Accelerated Sparsified SGD with Error Feedback

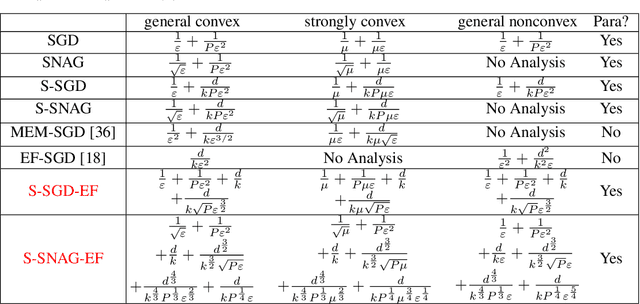
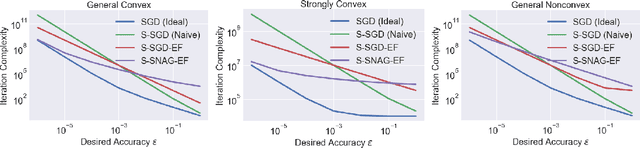
We study a stochastic gradient method for synchronous distributed optimization. For reducing communication cost, we are interested in utilizing compression of communicated gradients. Our main focus is a {\it{sparsified}} stochastic gradient method with {\it{error feedback}} scheme combined with {\it{Nesterov's acceleration}}. Strong theoretical analysis of sparsified SGD with error feedback in parallel computing settings and an application of acceleration scheme to sparsified SGD with error feedback are new. It is shown that (i) our method asymptotically achieves the same iteration complexity of non-sparsified SGD even in parallel computing settings; (ii) Nesterov's acceleration can improve the iteration complexity of non-accelerated methods in convex and even in nonconvex optimization problems for moderate optimization accuracy.