Normalized Maximum Likelihood Coding for Exponential Family with Its Applications to Optimal Clustering
Paper and Code
May 17, 2012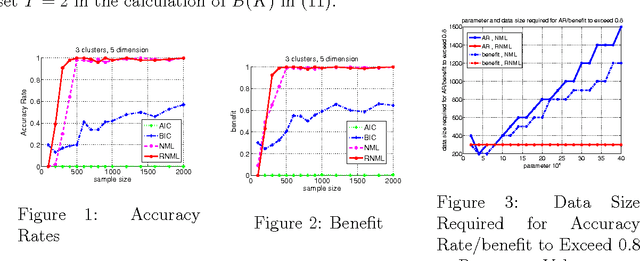
We are concerned with the issue of how to calculate the normalized maximum likelihood (NML) code-length. There is a problem that the normalization term of the NML code-length may diverge when it is continuous and unbounded and a straightforward computation of it is highly expensive when the data domain is finite . In previous works it has been investigated how to calculate the NML code-length for specific types of distributions. We first propose a general method for computing the NML code-length for the exponential family. Then we specifically focus on Gaussian mixture model (GMM), and propose a new efficient method for computing the NML to them. We develop it by generalizing Rissanen's re-normalizing technique. Then we apply this method to the clustering issue, in which a clustering structure is modeled using a GMM, and the main task is to estimate the optimal number of clusters on the basis of the NML code-length. We demonstrate using artificial data sets the superiority of the NML-based clustering over other criteria such as AIC, BIC in terms of the data size required for high accuracy rate to be achieved.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge