Learning Decision Trees and Forests with Algorithmic Recourse

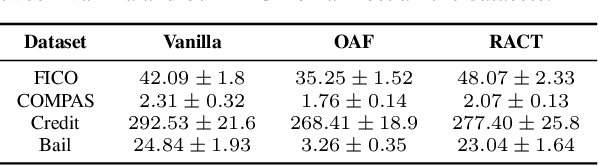
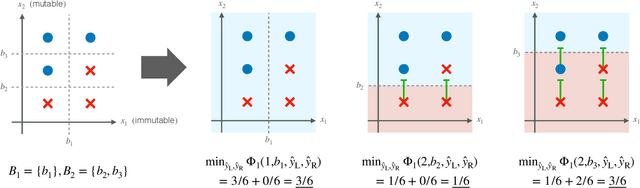
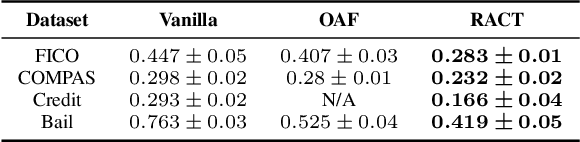
This paper proposes a new algorithm for learning accurate tree-based models while ensuring the existence of recourse actions. Algorithmic Recourse (AR) aims to provide a recourse action for altering the undesired prediction result given by a model. Typical AR methods provide a reasonable action by solving an optimization task of minimizing the required effort among executable actions. In practice, however, such actions do not always exist for models optimized only for predictive performance. To alleviate this issue, we formulate the task of learning an accurate classification tree under the constraint of ensuring the existence of reasonable actions for as many instances as possible. Then, we propose an efficient top-down greedy algorithm by leveraging the adversarial training techniques. We also show that our proposed algorithm can be applied to the random forest, which is known as a popular framework for learning tree ensembles. Experimental results demonstrated that our method successfully provided reasonable actions to more instances than the baselines without significantly degrading accuracy and computational efficiency.

Adaptive Topological Feature via Persistent Homology: Filtration Learning for Point Clouds

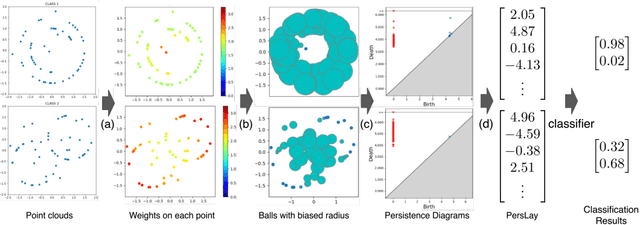
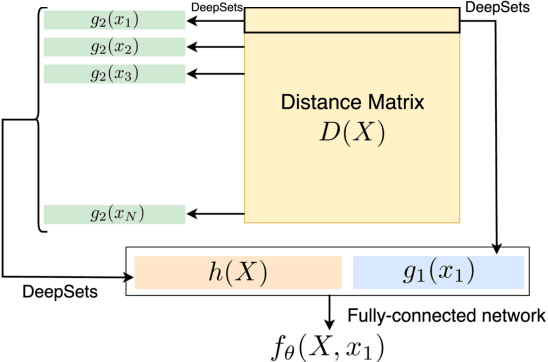
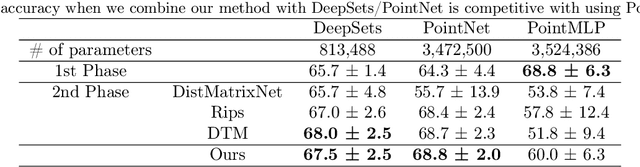
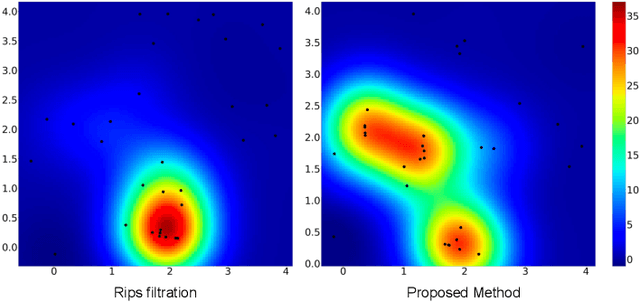
Machine learning for point clouds has been attracting much attention, with many applications in various fields, such as shape recognition and material science. To enhance the accuracy of such machine learning methods, it is known to be effective to incorporate global topological features, which are typically extracted by persistent homology. In the calculation of persistent homology for a point cloud, we need to choose a filtration for the point clouds, an increasing sequence of spaces. Because the performance of machine learning methods combined with persistent homology is highly affected by the choice of a filtration, we need to tune it depending on data and tasks. In this paper, we propose a framework that learns a filtration adaptively with the use of neural networks. In order to make the resulting persistent homology isometry-invariant, we develop a neural network architecture with such invariance. Additionally, we theoretically show a finite-dimensional approximation result that justifies our architecture. Experimental results demonstrated the efficacy of our framework in several classification tasks.

MAGDiff: Covariate Data Set Shift Detection via Activation Graphs of Deep Neural Networks

Despite their successful application to a variety of tasks, neural networks remain limited, like other machine learning methods, by their sensitivity to shifts in the data: their performance can be severely impacted by differences in distribution between the data on which they were trained and that on which they are deployed. In this article, we propose a new family of representations, called MAGDiff, that we extract from any given neural network classifier and that allows for efficient covariate data shift detection without the need to train a new model dedicated to this task. These representations are computed by comparing the activation graphs of the neural network for samples belonging to the training distribution and to the target distribution, and yield powerful data- and task-adapted statistics for the two-sample tests commonly used for data set shift detection. We demonstrate this empirically by measuring the statistical powers of two-sample Kolmogorov-Smirnov (KS) tests on several different data sets and shift types, and showing that our novel representations induce significant improvements over a state-of-the-art baseline relying on the network output.

Counterfactual Explanation with Missing Values

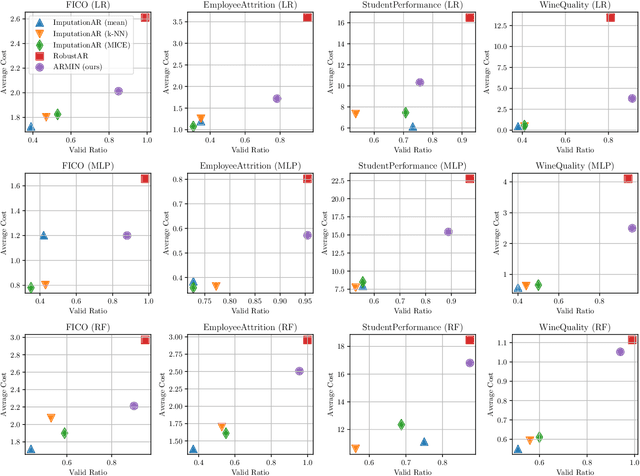
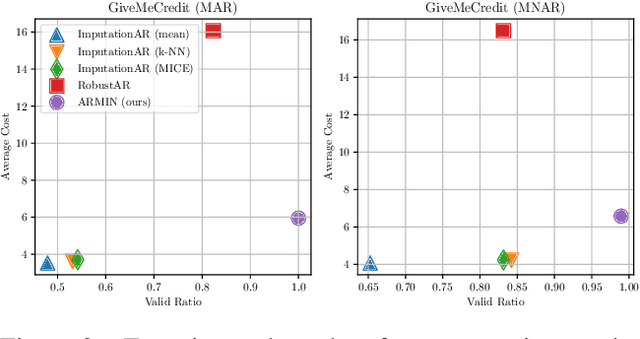
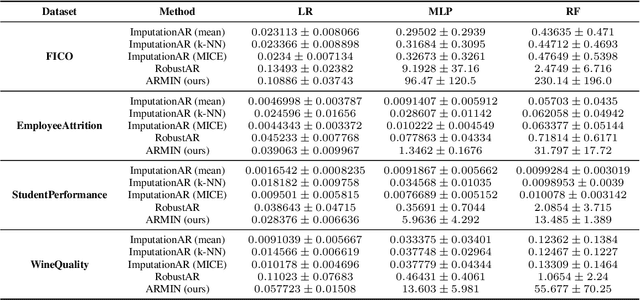
Counterfactual Explanation (CE) is a post-hoc explanation method that provides a perturbation for altering the prediction result of a classifier. Users can interpret the perturbation as an "action" to obtain their desired decision results. Existing CE methods require complete information on the features of an input instance. However, we often encounter missing values in a given instance, and the previous methods do not work in such a practical situation. In this paper, we first empirically and theoretically show the risk that missing value imputation methods affect the validity of an action, as well as the features that the action suggests changing. Then, we propose a new framework of CE, named Counterfactual Explanation by Pairs of Imputation and Action (CEPIA), that enables users to obtain valid actions even with missing values and clarifies how actions are affected by imputation of the missing values. Specifically, our CEPIA provides a representative set of pairs of an imputation candidate for a given incomplete instance and its optimal action. We formulate the problem of finding such a set as a submodular maximization problem, which can be solved by a simple greedy algorithm with an approximation guarantee. Experimental results demonstrated the efficacy of our CEPIA in comparison with the baselines in the presence of missing values.

Vanishing Component Analysis with Contrastive Normalization

Vanishing component analysis (VCA) computes approximate generators of vanishing ideals of samples, which are further used for extracting nonlinear features of the samples. Recent studies have shown that normalization of approximate generators plays an important role and different normalization leads to generators of different properties. In this paper, inspired by recent self-supervised frameworks, we propose a contrastive normalization method for VCA, where we impose the generators to vanish on the target samples and to be normalized on the transformed samples. We theoretically show that a contrastive normalization enhances the discriminative power of VCA, and provide the algebraic interpretation of VCA under our normalization. Numerical experiments demonstrate the effectiveness of our method. This is the first study to tailor the normalization of approximate generators of vanishing ideals to obtain discriminative features.

RipsNet: a general architecture for fast and robust estimation of the persistent homology of point clouds

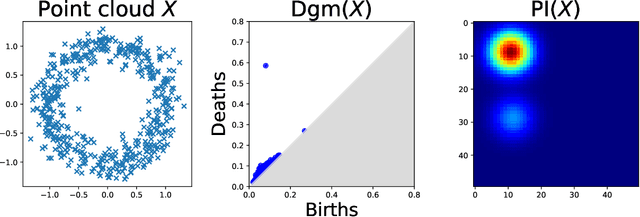
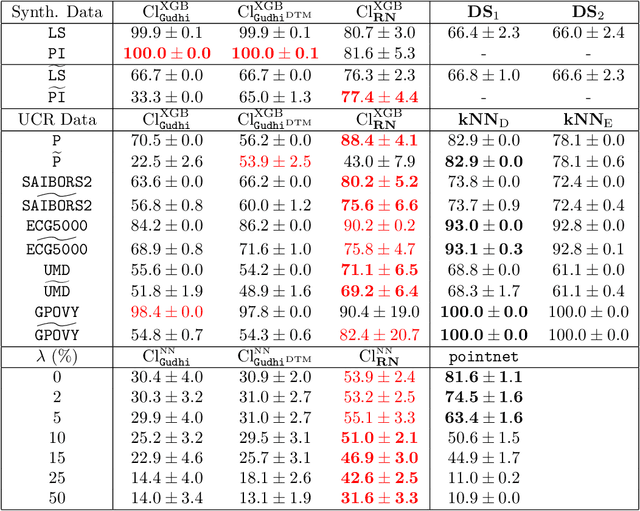
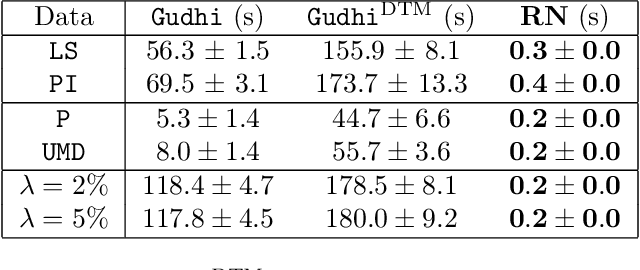
The use of topological descriptors in modern machine learning applications, such as Persistence Diagrams (PDs) arising from Topological Data Analysis (TDA), has shown great potential in various domains. However, their practical use in applications is often hindered by two major limitations: the computational complexity required to compute such descriptors exactly, and their sensitivity to even low-level proportions of outliers. In this work, we propose to bypass these two burdens in a data-driven setting by entrusting the estimation of (vectorization of) PDs built on top of point clouds to a neural network architecture that we call RipsNet. Once trained on a given data set, RipsNet can estimate topological descriptors on test data very efficiently with generalization capacity. Furthermore, we prove that RipsNet is robust to input perturbations in terms of the 1-Wasserstein distance, a major improvement over the standard computation of PDs that only enjoys Hausdorff stability, yielding RipsNet to substantially outperform exactly-computed PDs in noisy settings. We showcase the use of RipsNet on both synthetic and real-world data. Our open-source implementation is publicly available at https://github.com/hensel-f/ripsnet and will be included in the Gudhi library.

Topological Uncertainty: Monitoring trained neural networks through persistence of activation graphs

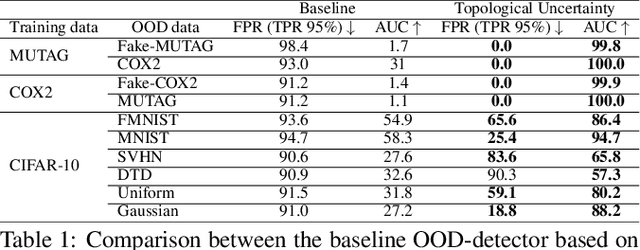
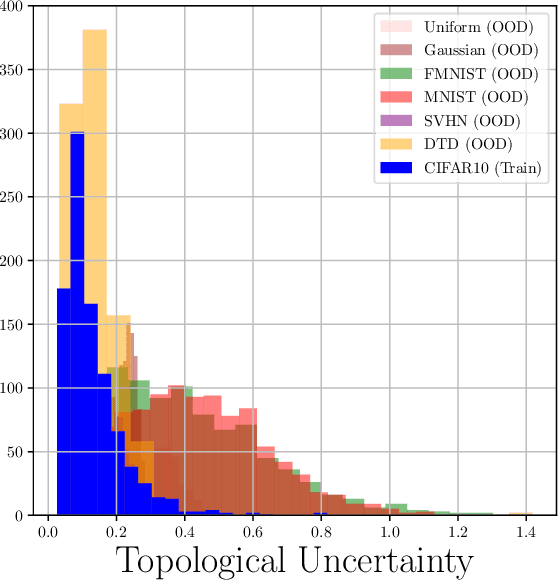
Although neural networks are capable of reaching astonishing performances on a wide variety of contexts, properly training networks on complicated tasks requires expertise and can be expensive from a computational perspective. In industrial applications, data coming from an open-world setting might widely differ from the benchmark datasets on which a network was trained. Being able to monitor the presence of such variations without retraining the network is of crucial importance. In this article, we develop a method to monitor trained neural networks based on the topological properties of their activation graphs. To each new observation, we assign a Topological Uncertainty, a score that aims to assess the reliability of the predictions by investigating the whole network instead of its final layer only, as typically done by practitioners. Our approach entirely works at a post-training level and does not require any assumption on the network architecture, optimization scheme, nor the use of data augmentation or auxiliary datasets; and can be faithfully applied on a large range of network architectures and data types. We showcase experimentally the potential of Topological Uncertainty in the context of trained network selection, Out-Of-Distribution detection, and shift-detection, both on synthetic and real datasets of images and graphs.

Ordered Counterfactual Explanation by Mixed-Integer Linear Optimization

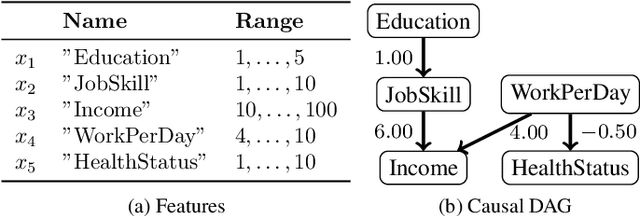
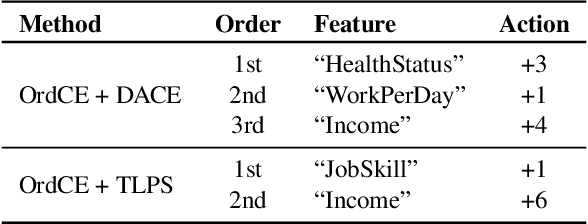
Post-hoc explanation methods for machine learning models have been widely used to support decision-making. One of the popular methods is Counterfactual Explanation (CE), which provides a user with a perturbation vector of features that alters the prediction result. Given a perturbation vector, a user can interpret it as an "action" for obtaining one's desired decision result. In practice, however, showing only a perturbation vector is often insufficient for users to execute the action. The reason is that if there is an asymmetric interaction among features, such as causality, the total cost of the action is expected to depend on the order of changing features. Therefore, practical CE methods are required to provide an appropriate order of changing features in addition to a perturbation vector. For this purpose, we propose a new framework called Ordered Counterfactual Explanation (OrdCE). We introduce a new objective function that evaluates a pair of an action and an order based on feature interaction. To extract an optimal pair, we propose a mixed-integer linear optimization approach with our objective function. Numerical experiments on real datasets demonstrated the effectiveness of our OrdCE in comparison with unordered CE methods.

ATOL: Automatic Topologically-Oriented Learning

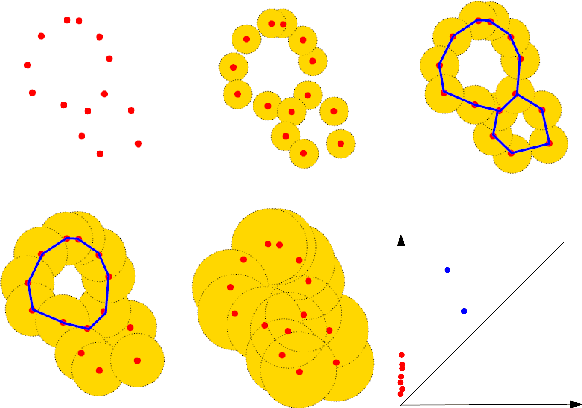
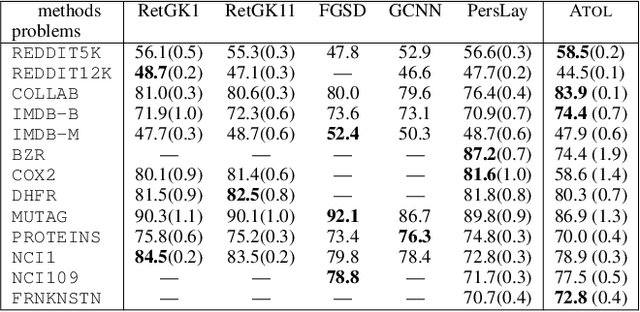
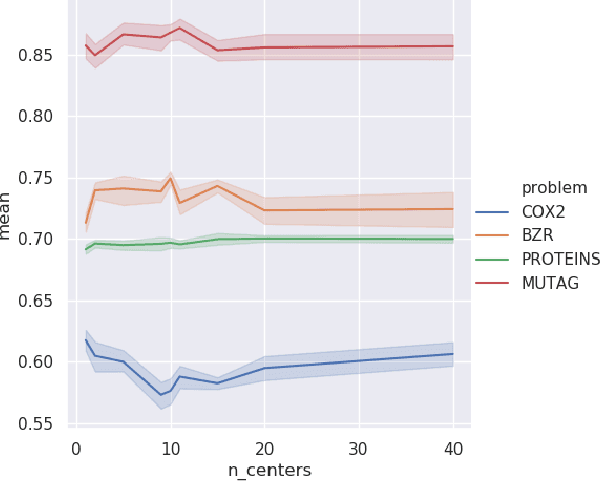
There are abundant cases for using Topological Data Analysis (TDA) in a learning context, but robust topological information commonly comes in the form of a set of persistence diagrams, objects that by nature are uneasy to affix to a generic machine learning framework. We introduce a vectorisation method for diagrams that allows to collect information from topological descriptors into a format fit for machine learning tools. Based on a few observations, the method is learned and tailored to discriminate the various important plane regions a diagram is set into. With this tool one can automatically augment any sort of machine learning problem with access to a TDA method, enhance performances, construct features reflecting underlying changes in topological behaviour. The proposed methodology comes with only high level tuning parameters such as the encoding budget for topological features. We provide an open-access, ready-to-use implementation and notebook. We showcase the strengths and versatility of our approach on a number of applications. From emulous and modern graph collections to a highly topological synthetic dynamical orbits data, we prove that the method matches or beats the state-of-the-art in encoding persistence diagrams to solve hard problems. We then apply our method in the context of an industrial, difficult time-series regression problem and show the approach to be relevant.

PersLay: A Simple and Versatile Neural Network Layer for Persistence Diagrams

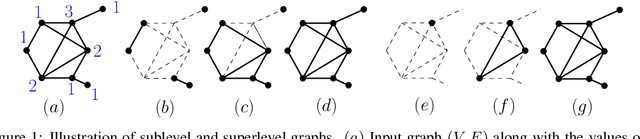
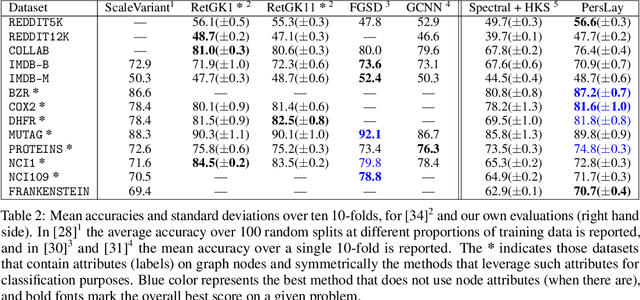
Persistence diagrams, a key descriptor from Topological Data Analysis, encode and summarize all sorts of topological features and have already proved pivotal in many different applications of data science. But persistence diagrams are weakly structured and therefore constitute a difficult input for most Machine Learning techniques. To address this concern several vectorization methods have been put forward that embed persistence diagrams into either finite-dimensional Euclidean spaces or implicit Hilbert spaces with kernels. But finite-dimensional embeddings are prone to miss a lot of information about persistence diagrams, while kernel methods require the full computation of the kernel matrix. We introduce PersLay: a simple, highly modular layer of learning architecture for persistence diagrams that allows to exploit the full capacities of neural networks on topological information from any dataset. This layer encompasses most of the vectorization methods of the literature. We illustrate its strengths on challenging classification problems on dynamical systems orbit or real-life graph data, with results improving or comparable to the state-of-the-art. In order to exploit topological information from graph data, we show how graph structures can be encoded in the so-called extended persistence diagrams computed with the heat kernel signatures of the graphs.