Resampling and averaging coordinates on data

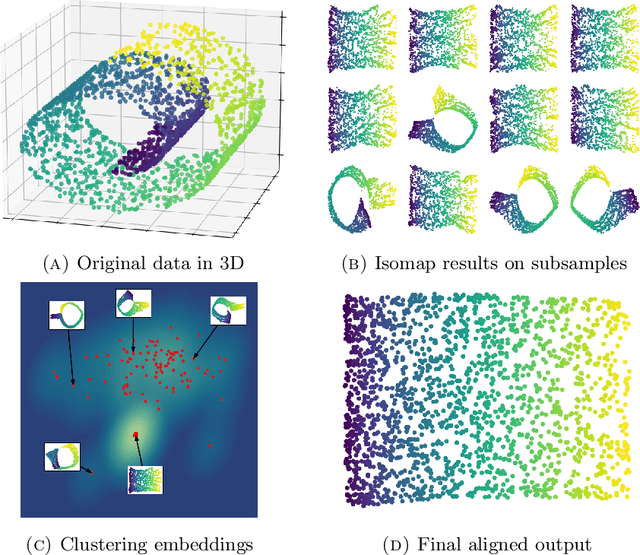
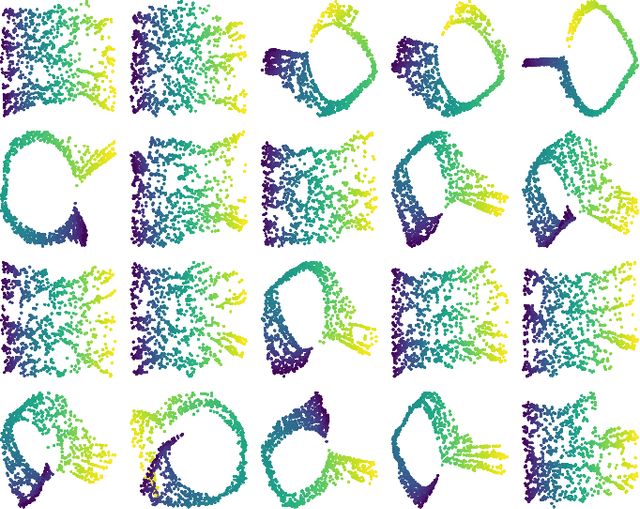
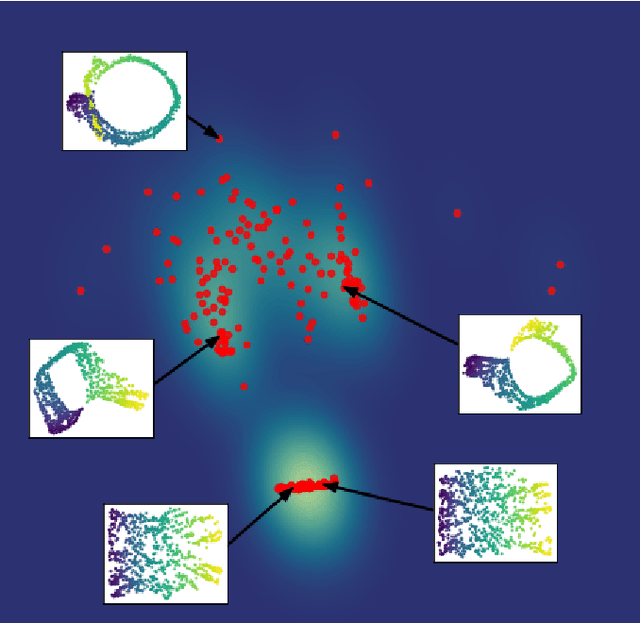
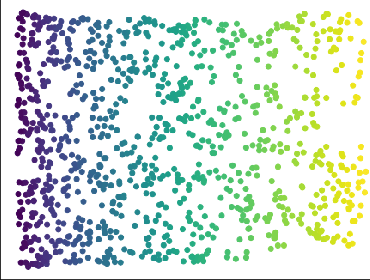
We introduce algorithms for robustly computing intrinsic coordinates on point clouds. Our approach relies on generating many candidate coordinates by subsampling the data and varying hyperparameters of the embedding algorithm (e.g., manifold learning). We then identify a subset of representative embeddings by clustering the collection of candidate coordinates and using shape descriptors from topological data analysis. The final output is the embedding obtained as an average of the representative embeddings using generalized Procrustes analysis. We validate our algorithm on both synthetic data and experimental measurements from genomics, demonstrating robustness to noise and outliers.

Diffeomorphic interpolation for efficient persistence-based topological optimization

Topological Data Analysis (TDA) provides a pipeline to extract quantitative topological descriptors from structured objects. This enables the definition of topological loss functions, which assert to what extent a given object exhibits some topological properties. These losses can then be used to perform topological optimizationvia gradient descent routines. While theoretically sounded, topological optimization faces an important challenge: gradients tend to be extremely sparse, in the sense that the loss function typically depends on only very few coordinates of the input object, yielding dramatically slow optimization schemes in practice.Focusing on the central case of topological optimization for point clouds, we propose in this work to overcome this limitation using diffeomorphic interpolation, turning sparse gradients into smooth vector fields defined on the whole space, with quantifiable Lipschitz constants. In particular, we show that our approach combines efficiently with subsampling techniques routinely used in TDA, as the diffeomorphism derived from the gradient computed on a subsample can be used to update the coordinates of the full input object, allowing us to perform topological optimization on point clouds at an unprecedented scale. Finally, we also showcase the relevance of our approach for black-box autoencoder (AE) regularization, where we aim at enforcing topological priors on the latent spaces associated to fixed, pre-trained, black-box AE models, and where we show thatlearning a diffeomorphic flow can be done once and then re-applied to new data in linear time (while vanilla topological optimization has to be re-run from scratch). Moreover, reverting the flow allows us to generate data by sampling the topologically-optimized latent space directly, yielding better interpretability of the model.

Topological Uncertainty: Monitoring trained neural networks through persistence of activation graphs

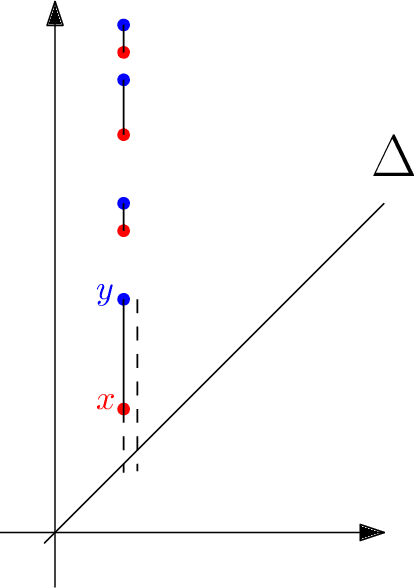
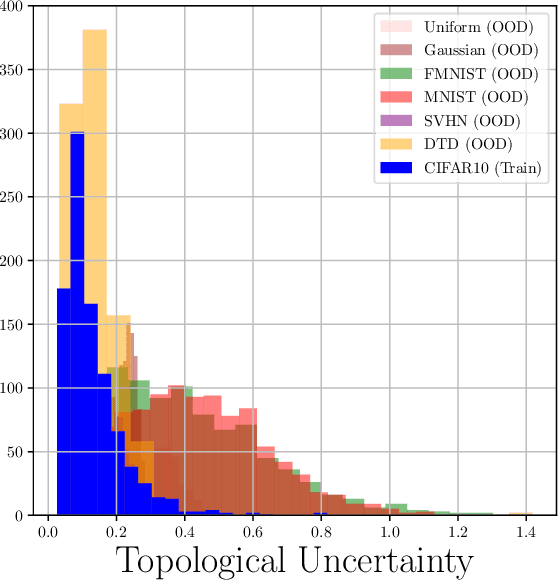
Although neural networks are capable of reaching astonishing performances on a wide variety of contexts, properly training networks on complicated tasks requires expertise and can be expensive from a computational perspective. In industrial applications, data coming from an open-world setting might widely differ from the benchmark datasets on which a network was trained. Being able to monitor the presence of such variations without retraining the network is of crucial importance. In this article, we develop a method to monitor trained neural networks based on the topological properties of their activation graphs. To each new observation, we assign a Topological Uncertainty, a score that aims to assess the reliability of the predictions by investigating the whole network instead of its final layer only, as typically done by practitioners. Our approach entirely works at a post-training level and does not require any assumption on the network architecture, optimization scheme, nor the use of data augmentation or auxiliary datasets; and can be faithfully applied on a large range of network architectures and data types. We showcase experimentally the potential of Topological Uncertainty in the context of trained network selection, Out-Of-Distribution detection, and shift-detection, both on synthetic and real datasets of images and graphs.

MREC: a fast and versatile framework for aligning and matching point clouds with applications to single cell molecular data

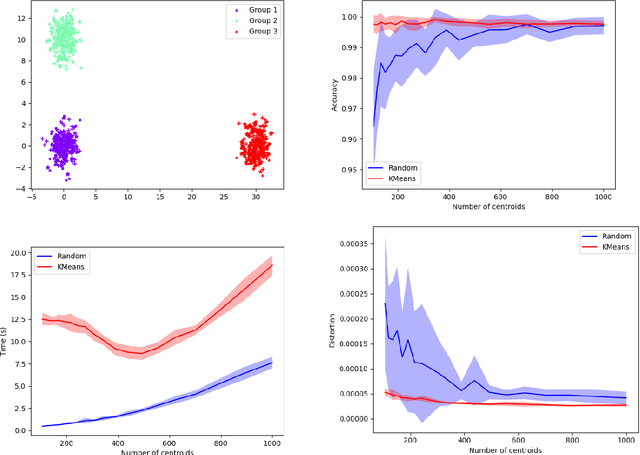
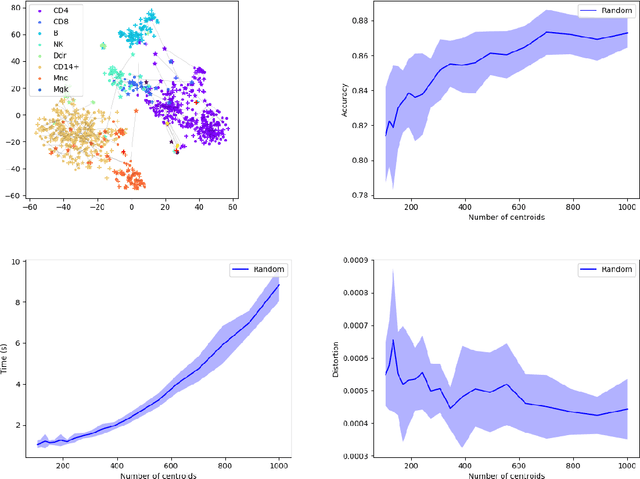
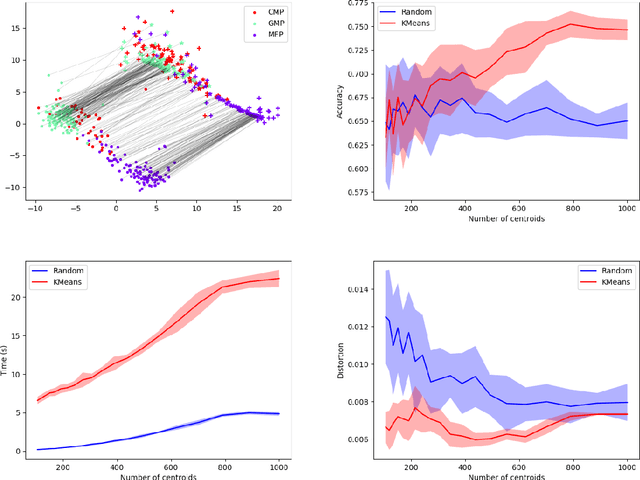
Comparing and aligning large datasets is a pervasive problem occurring across many different knowledge domains. We introduce and study MREC, a recursive decomposition algorithm for computing matchings between data sets. The basic idea is to partition the data, match the partitions, and then recursively match the points within each pair of identified partitions. The matching itself is done using black box matching procedures that are too expensive to run on the entire data set. Using an absolute measure of the quality of a matching, the framework supports optimization over parameters including partitioning procedures and matching algorithms. By design, MREC can be applied to extremely large data sets. We analyze the procedure to describe when we can expect it to work well and demonstrate its flexibility and power by applying it to a number of alignment problems arising in the analysis of single cell molecular data.

On the Metric Distortion of Embedding Persistence Diagrams into Reproducing Kernel Hilbert Spaces

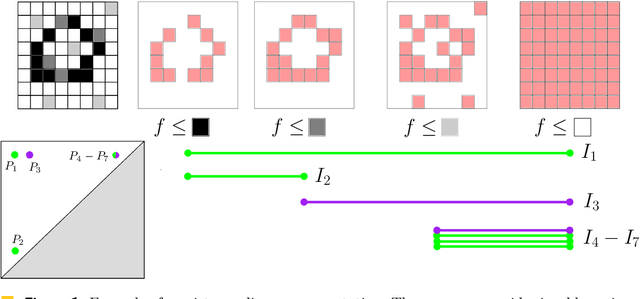
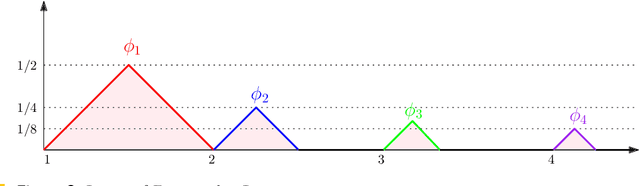
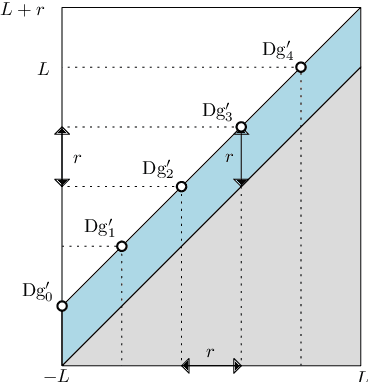
Persistence diagrams are important feature descriptors in Topological Data Analysis. Due to the nonlinearity of the space of persistence diagrams equipped with their {\em diagram distances}, most of the recent attempts at using persistence diagrams in Machine Learning have been done through kernel methods, i.e., embeddings of persistence diagrams into Reproducing Kernel Hilbert Spaces (RKHS), in which all computations can be performed easily. Since persistence diagrams enjoy theoretical stability guarantees for the diagram distances, the {\em metric properties} of a kernel $k$, i.e., the relationship between the RKHS distance $d_k$ and the diagram distances, are of central interest for understanding if the persistence diagram guarantees carry over to the embedding. In this article, we study the possibility of embedding persistence diagrams into RKHS with bi-Lipschitz maps. In particular, we show that when the RKHS is infinite dimensional, any lower bound must depend on the cardinalities of the persistence diagrams, and that when the RKHS is finite dimensional, finding a bi-Lipschitz embedding is impossible, even when restricting the persistence diagrams to have bounded cardinalities.