Recovering Manifold Structure Using Ollivier-Ricci Curvature

We introduce ORC-ManL, a new algorithm to prune spurious edges from nearest neighbor graphs using a criterion based on Ollivier-Ricci curvature and estimated metric distortion. Our motivation comes from manifold learning: we show that when the data generating the nearest-neighbor graph consists of noisy samples from a low-dimensional manifold, edges that shortcut through the ambient space have more negative Ollivier-Ricci curvature than edges that lie along the data manifold. We demonstrate that our method outperforms alternative pruning methods and that it significantly improves performance on many downstream geometric data analysis tasks that use nearest neighbor graphs as input. Specifically, we evaluate on manifold learning, persistent homology, dimension estimation, and others. We also show that ORC-ManL can be used to improve clustering and manifold learning of single-cell RNA sequencing data. Finally, we provide empirical convergence experiments that support our theoretical findings.

Resampling and averaging coordinates on data

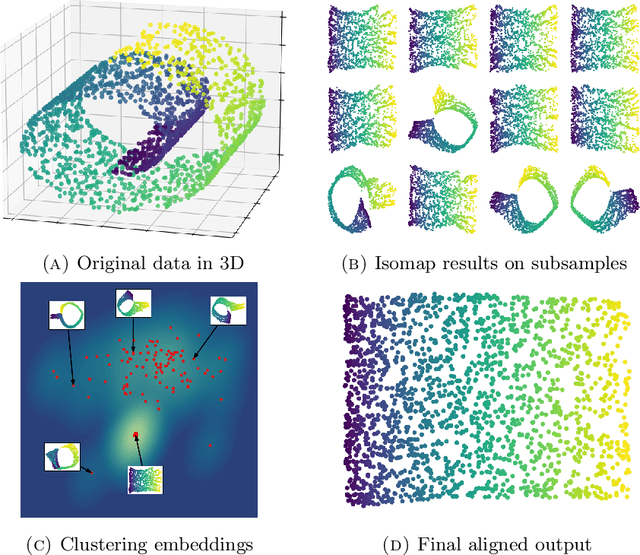
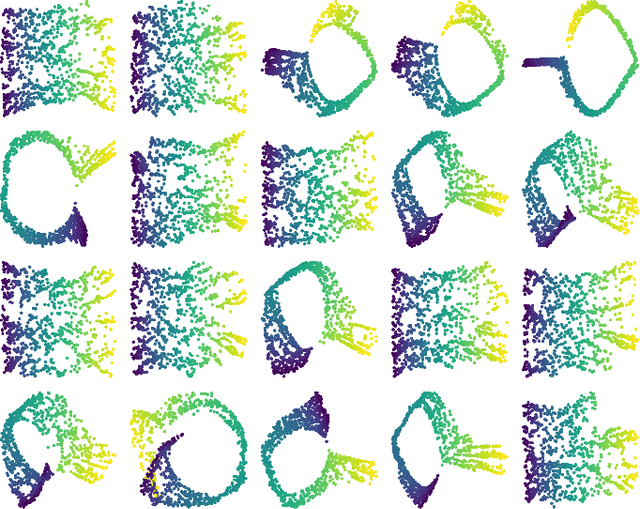
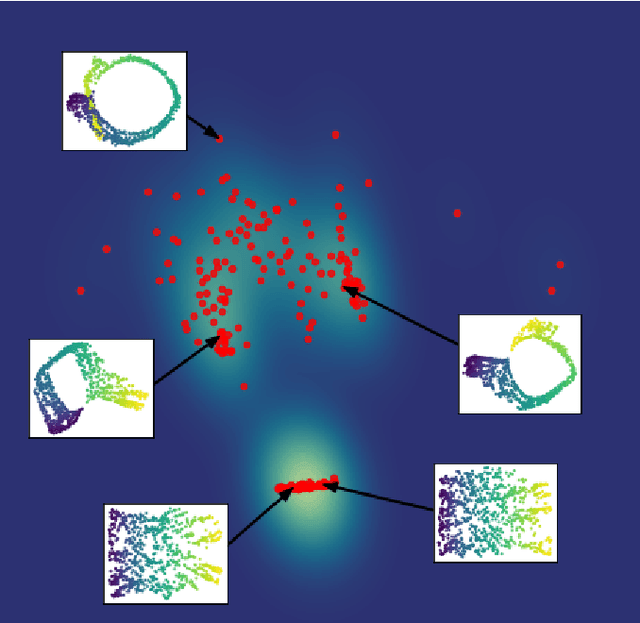
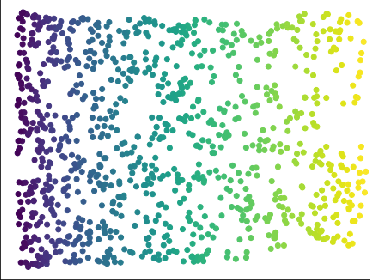
We introduce algorithms for robustly computing intrinsic coordinates on point clouds. Our approach relies on generating many candidate coordinates by subsampling the data and varying hyperparameters of the embedding algorithm (e.g., manifold learning). We then identify a subset of representative embeddings by clustering the collection of candidate coordinates and using shape descriptors from topological data analysis. The final output is the embedding obtained as an average of the representative embeddings using generalized Procrustes analysis. We validate our algorithm on both synthetic data and experimental measurements from genomics, demonstrating robustness to noise and outliers.

An Intrinsic Approach to Scalar-Curvature Estimation for Point Clouds

We introduce an intrinsic estimator for the scalar curvature of a data set presented as a finite metric space. Our estimator depends only on the metric structure of the data and not on an embedding in $\mathbb{R}^n$. We show that the estimator is consistent in the sense that for points sampled from a probability measure on a compact Riemannian manifold, the estimator converges to the scalar curvature as the number of points increases. To justify its use in applications, we show that the estimator is stable with respect to perturbations of the metric structure, e.g., noise in the sample or error estimating the intrinsic metric. We validate our estimator experimentally on synthetic data that is sampled from manifolds with specified curvature.

A Framework for Fast and Stable Representations of Multiparameter Persistent Homology Decompositions

Topological data analysis (TDA) is an area of data science that focuses on using invariants from algebraic topology to provide multiscale shape descriptors for geometric data sets such as point clouds. One of the most important such descriptors is {\em persistent homology}, which encodes the change in shape as a filtration parameter changes; a typical parameter is the feature scale. For many data sets, it is useful to simultaneously vary multiple filtration parameters, for example feature scale and density. While the theoretical properties of single parameter persistent homology are well understood, less is known about the multiparameter case. In particular, a central question is the problem of representing multiparameter persistent homology by elements of a vector space for integration with standard machine learning algorithms. Existing approaches to this problem either ignore most of the multiparameter information to reduce to the one-parameter case or are heuristic and potentially unstable in the face of noise. In this article, we introduce a new general representation framework that leverages recent results on {\em decompositions} of multiparameter persistent homology. This framework is rich in information, fast to compute, and encompasses previous approaches. Moreover, we establish theoretical stability guarantees under this framework as well as efficient algorithms for practical computation, making this framework an applicable and versatile tool for analyzing geometric and point cloud data. We validate our stability results and algorithms with numerical experiments that demonstrate statistical convergence, prediction accuracy, and fast running times on several real data sets.

MREC: a fast and versatile framework for aligning and matching point clouds with applications to single cell molecular data

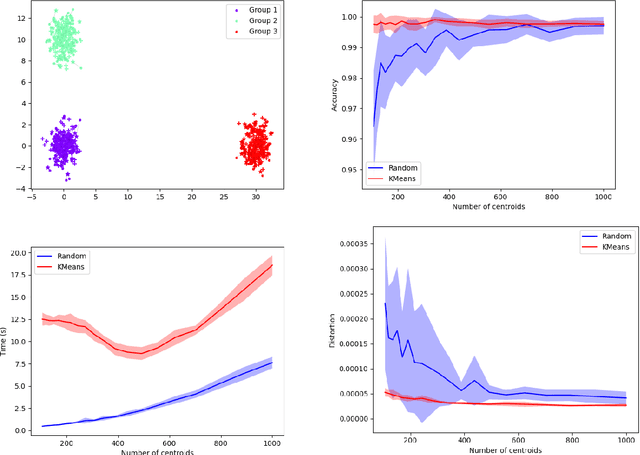
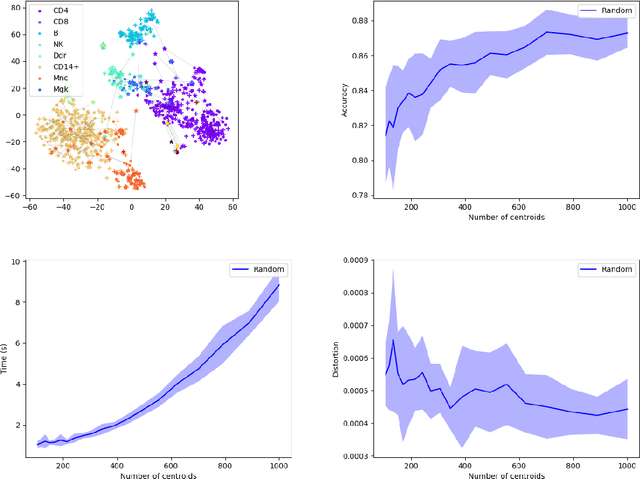
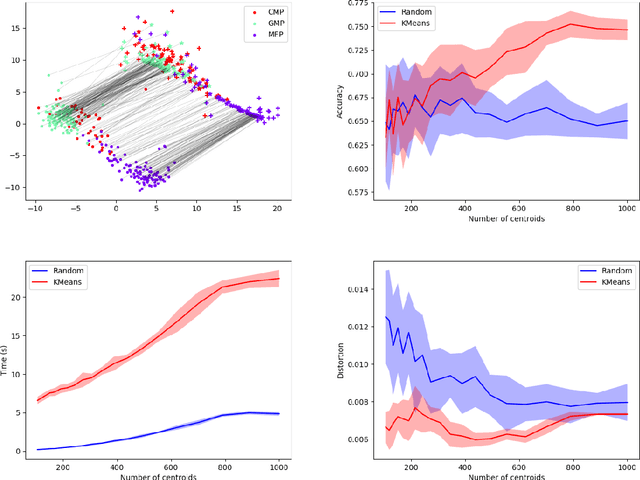
Comparing and aligning large datasets is a pervasive problem occurring across many different knowledge domains. We introduce and study MREC, a recursive decomposition algorithm for computing matchings between data sets. The basic idea is to partition the data, match the partitions, and then recursively match the points within each pair of identified partitions. The matching itself is done using black box matching procedures that are too expensive to run on the entire data set. Using an absolute measure of the quality of a matching, the framework supports optimization over parameters including partitioning procedures and matching algorithms. By design, MREC can be applied to extremely large data sets. We analyze the procedure to describe when we can expect it to work well and demonstrate its flexibility and power by applying it to a number of alignment problems arising in the analysis of single cell molecular data.

Testing to distinguish measures on metric spaces

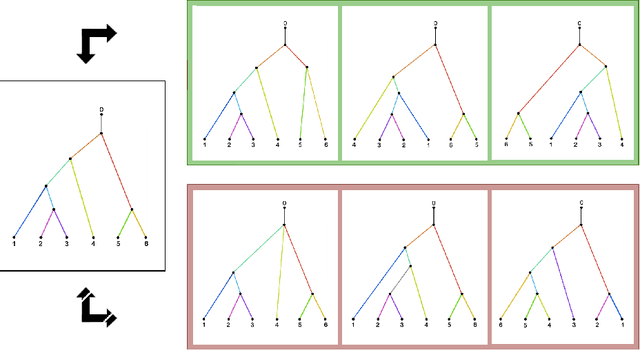
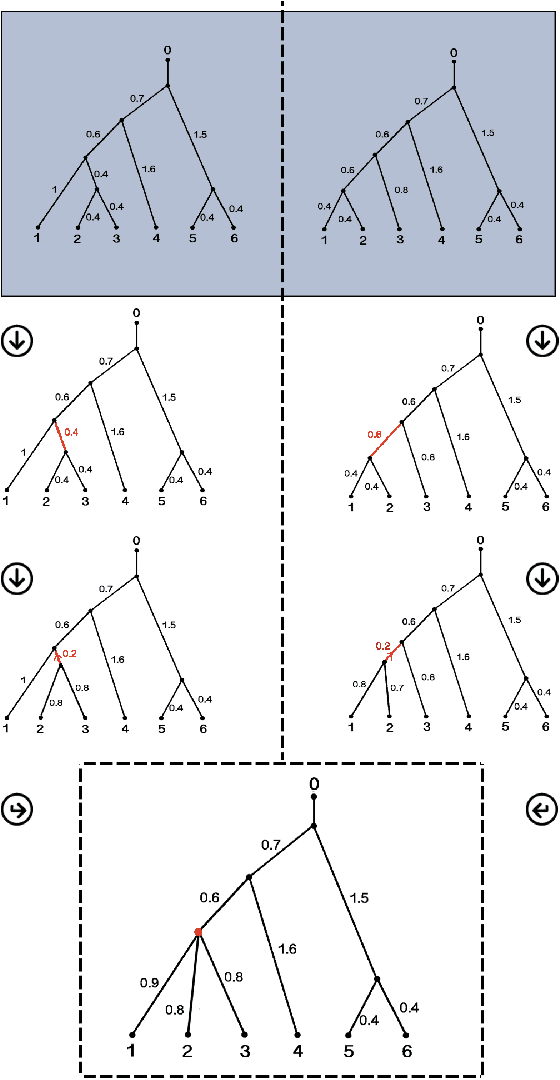
We study the problem of distinguishing between two distributions on a metric space; i.e., given metric measure spaces $({\mathbb X}, d, \mu_1)$ and $({\mathbb X}, d, \mu_2)$, we are interested in the problem of determining from finite data whether or not $\mu_1$ is $\mu_2$. The key is to use pairwise distances between observations and, employing a reconstruction theorem of Gromov, we can perform such a test using a two sample Kolmogorov--Smirnov test. A real analysis using phylogenetic trees and flu data is presented.

A polynomial-time relaxation of the Gromov-Hausdorff distance

The Gromov-Hausdorff distance provides a metric on the set of isometry classes of compact metric spaces. Unfortunately, computing this metric directly is believed to be computationally intractable. Motivated by applications in shape matching and point-cloud comparison, we study a semidefinite programming relaxation of the Gromov-Hausdorff metric. This relaxation can be computed in polynomial time, and somewhat surprisingly is itself a pseudometric. We describe the induced topology on the set of compact metric spaces. Finally, we demonstrate the numerical performance of various algorithms for computing the relaxed distance and apply these algorithms to several relevant data sets. In particular we propose a greedy algorithm for finding the best correspondence between finite metric spaces that can handle hundreds of points.